기울기 (벡터)

물매는 여기로 연결됩니다. 무기에 대해서는 무릿매 문서를 참고하십시오.

기울기(gradient 그레이디언트^[*]) 또는 경도란 벡터 미적분학에서 스칼라장의 최대의 증가율을 나타내는 벡터장을 뜻한다.

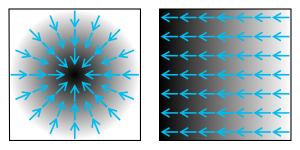
위의 두 그림에서는 회색의 밝기가 스칼라계의 크기를 뜻한다. 짙은 색일수록 크기가 큰데, 스칼라계의 기울기는 파란색 화살표로 나타냈다.

기울기를 나타내는 벡터장을 화살표로 표시할 때 화살표의 방향은 증가율이 최대가 되는 방향이며, 화살표의 크기는 증가율이 최대일 때의 증가율의 크기를 나타낸다.

기울기의 의미

어느 방안의 공간 온도 분포가 스칼라장 φ로 주어졌다고 가정한다. 이 때, 방안의 어느 한 점(x,y,z)에서의 온도는 φ(x,y,z)로 표시할 수 있다. (온도는 시간에 의해 변화하지 않는다고 가정) 이 경우에 어느 한 지점에서의 기울기는 온도가 가장 빨리 증가하는 방향과 그 증가율을 나타낸다.

이번에는 산이나 언덕을 가정해보자. 어떤 지점(x,y)에서의 높이를 H(x,y)로 표현하는 경우, 기울기는 가장 (위를 바라보는)경사가 가파른 방향과 그 경사의 크기를 나타낸다.

기울기를 이용해 다른 방향의 증가율을 구하려면 기울기와 그 방향의 단위 벡터의 내적을 취하면 된다.

기울기는 무회전성 벡터계이다. 즉, 기울기 벡터계에 대해 선적분을 구하면 결과값은 경로와 상관없이 시작점과 끝점에 따라서만 변화함을 뜻한다.

기울기의 수학적 정의

스칼라 함수 $f(x)$의 기울기는 ${\boldsymbol {\nabla }}f$로 표현한다. $\nabla$ 기호는 벡터 미분 연산자로 나블라(nabla) 혹은 델(del)연산자라고 부른다.

기울기는 $f$의 각 성분의 편미분으로 구성된 열벡터로 정의하며 다음과 같이 표시한다.

${\boldsymbol {\nabla }}f=\left({\frac {\partial f}{\partial x_{1}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right)$

${\boldsymbol {\nabla }}f=\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}}\right)$

예를 들어 함수

$f(x,y,z)=\ 2x+3y^{2}-\sin(z)$의 기울기는

${\boldsymbol {\nabla }}f={\begin{pmatrix}{\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\end{pmatrix}}={\begin{pmatrix}{2},{6y},{-\cos(z)}\end{pmatrix}}$이다.

성질

• 그래디언트는 등위선과 직교한다.

${\boldsymbol {\nabla }}f\bot L_{c}(f).\quad L_{c}(f)=\left\{\mathbf {r} (t)|f(\mathbf {r} (t))=c\right\}$

증명

등위집합은 다음과 같이 정의된다. 함수 $f$의 값을 일정하게 하는 곡선상을 매개변수 $t$를 이용한 벡터 $\mathbf {r}$로 나타낸다.

$L_{c}(f)=\left\{\mathbf {r} (t)=(x_{1},x_{2},...,x_{n})|f(\mathbf {r} (t))=c\right\}$

등위집합의 접선벡터는 $\mathbf {r} '(t)=\lim _{\Delta t\to 0}{\frac {\mathbf {r} (t+\Delta t)-\mathbf {r} (t)}{\Delta t}}$이 된다. 한편 $g(t)=f(\mathbf {r} (t))=c$라 할 때

$g'(t)={\frac {\partial f}{\partial x_{1}}}{\frac {dx_{1}}{dt}}+{\frac {\partial f}{\partial x_{2}}}{\frac {dx_{2}}{dt}}+...+{\frac {\partial f}{\partial x_{n}}}{\frac {dx_{n}}{dt}}={\boldsymbol {\nabla }}f\cdot \mathbf {r} '(t)=0$

따라서 그래디언트와 등위선은 직교한다.

같이 보기

• 회전 (벡터)
• 발산 (벡터)