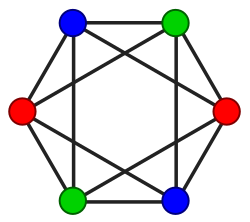
그래프 이론 에서 그래프 색칠 (graph色漆, 영어 : graph colo(u)ring )은 그래프 의 꼭지점들에, 같은 색이 인접하지 않도록 색을 부여하는 방법이다. 이를 사용하여 그래프의 불변량을 정의할 수 있다.
그래프의 3개의 색으로의 색칠. 이 그래프는 2개의 색으로 색칠할 수 없으며, 따라서 이 그래프의 색칠수는 3이다.
(단순) 그래프
G
{\displaystyle G}
색칠
(
C
,
c
)
{\displaystyle (C,c)}
C
{\displaystyle C}
c
:
V
(
G
)
→
C
{\displaystyle c\colon V(G)\to C}
v
1
v
2
∈
E
(
G
)
{\displaystyle v_{1}v_{2}\in E(G)}
c
(
v
1
)
≠
c
(
v
2
)
{\displaystyle c(v_{1})\neq c(v_{2})}
(
C
,
c
)
{\displaystyle (C,c)}
C
{\displaystyle C}
색 (色, 영어 : colo(u)r )이라고 한다.
그래프
G
{\displaystyle G}
(
C
,
c
)
{\displaystyle (C,c)}
(
C
′
,
c
′
)
{\displaystyle (C',c')}
전단사 함수
f
:
C
→
C
′
{\displaystyle f\colon C\to C'}
c
′
=
f
∘
c
{\displaystyle c'=f\circ c}
동형 이라고 한다.
그래프
G
{\displaystyle G}
변 색칠 영어 : edge colo(u)ring )은
G
{\displaystyle G}
선 그래프
L
(
G
)
{\displaystyle L(G)}
평면 그래프
G
{\displaystyle G}
면 색칠 (面色漆, 영어 : face colo(u)ring )은 그 쌍대 그래프 (영어 : dual graph )
G
′
{\displaystyle G'}
이 그래프
G
{\displaystyle G}
P
G
a
(
3
)
=
12
{\displaystyle P_{G}a(3)=12}
그래프
G
{\displaystyle G}
C
=
{
1
,
2
,
…
,
t
}
{\displaystyle C=\{1,2,\dots ,t\}}
P
G
(
t
)
{\displaystyle P_{G}(t)}
G
{\displaystyle G}
t
{\displaystyle t}
다항식 을 이루며, 이를
G
{\displaystyle G}
색칠 다항식 (영어 : chromatic polynomial )이라고 한다. 그래프
G
{\displaystyle G}
색칠수 (色漆數, 영어 : chromatic number )
χ
(
G
)
{\displaystyle \chi (G)}
χ
(
G
)
=
min
{
t
∈
N
:
P
G
(
t
)
>
0
}
{\displaystyle \chi (G)=\min\{t\in \mathbb {N} \colon P_{G}(t)>0\}}
마찬가지로, 변 색칠 다항식 · 변 색칠수 따위를 정의할 수 있다. 변 색칠수는 색칠 지표 (영어 : chromatic index )라고도 하며,
χ
′
(
G
)
{\displaystyle \chi '(G)}
(단순) 유한 그래프
G
{\displaystyle G}
동치 다.
χ
(
G
)
=
1
{\displaystyle \chi (G)=1}
P
G
(
t
)
=
t
n
{\displaystyle P_{G}(t)=t^{n}}
n
∈
Z
+
{\displaystyle n\in \mathbb {Z} ^{+}}
|
E
(
G
)
|
=
0
{\displaystyle |E(G)|=0}
|
V
(
G
)
|
≥
1
{\displaystyle |V(G)|\geq 1}
(단순) 그래프
G
{\displaystyle G}
동치 다.
χ
(
G
)
=
2
{\displaystyle \chi (G)=2}
G
{\displaystyle G}
이분 그래프 이다.모든 (단순) 유한 그래프
G
{\displaystyle G}
1
≤
χ
(
G
)
≤
|
V
(
G
)
|
{\displaystyle 1\leq \chi (G)\leq |V(G)|}
χ
(
G
)
(
χ
(
G
)
−
1
)
≤
2
|
E
(
G
)
|
{\displaystyle \chi (G)\left(\chi (G)-1\right)\leq 2|E(G)|}
ω
(
G
)
≤
χ
(
G
)
≤
Δ
(
G
)
+
1
{\displaystyle \omega (G)\leq \chi (G)\leq \Delta (G)+1}
여기서
ω
(
G
)
{\displaystyle \omega (G)}
G
{\displaystyle G}
클릭 의 크기이며,
Δ
(
G
)
=
max
v
∈
V
(
G
)
deg
v
{\displaystyle \Delta (G)=\max _{v\in V(G)}\deg v}
G
{\displaystyle G}
브룩스의 정리 (영어 : Brooks’ theorem )에 따르면, 임의의 연결 유한 그래프
G
{\displaystyle G}
동치 이다.
χ
(
G
)
=
Δ
(
G
)
+
1
{\displaystyle \chi (G)=\Delta (G)+1}
G
{\displaystyle G}
완벽 그래프 이거나 홀수 크기의 순환 그래프 이다.4색정리 평면 그래프
G
{\displaystyle G}
χ
(
G
)
≤
4
{\displaystyle \chi (G)\leq 4}
이다. 그뢰치의 정리 (영어 : Grötzsch’s theorem )에 따르면, 크기가 3인 순환 을 갖지 않는 유한 평면 그래프
G
{\displaystyle G}
χ
(
G
)
≤
3
{\displaystyle \chi (G)\leq 3}
이다.
n
{\displaystyle n}
n
{\displaystyle n}
(단순) 유한 그래프
G
{\displaystyle G}
χ
G
(
t
)
=
t
(
t
−
1
)
n
−
1
{\displaystyle \chi _{G}(t)=t(t-1)^{n-1}}
G
{\displaystyle G}
n
{\displaystyle n}
나무 이다.(단순) 유한 그래프
G
{\displaystyle G}
χ
G
(
t
)
=
(
t
−
1
)
n
+
(
−
1
)
n
(
t
−
1
)
{\displaystyle \chi _{G}(t)=(t-1)^{n}+(-1)^{n}(t-1)}
G
{\displaystyle G}
n
{\displaystyle n}
순환 그래프
C
n
{\displaystyle C_{n}}
색칠 다항식이
t
(
t
−
1
)
3
(
t
−
2
)
{\displaystyle t(t-1)^{3}(t-2)}
두 그래프의 색칠 다항식이 같을 경우, 이들이 색칠 동치 (영어 : chromatically equivalent )라고 한다. 서로 동형이 아닌 두 그래프가 색칠 동치일 수 있다. 예를 들어, 꼭짓점의 수가 같지만 서로 동형이 아닌 두 나무 는 색칠 동치이다. 또한, 색칠 다항식이
t
(
t
−
1
)
3
(
t
−
2
)
{\displaystyle t(t-1)^{3}(t-2)}
연결 성분
G
1
,
…
,
G
n
{\displaystyle G_{1},\dots ,G_{n}}
P
G
(
t
)
=
∏
i
=
1
n
P
G
i
(
t
)
{\displaystyle P_{G}(t)=\prod _{i=1}^{n}P_{G_{i}}(t)}
(단순) 그래프
G
{\displaystyle G}
u
v
∈
E
(
G
)
{\displaystyle uv\in E(G)}
G
−
u
v
{\displaystyle G-uv}
G
{\displaystyle G}
u
v
{\displaystyle uv}
G
/
u
v
{\displaystyle G/uv}
G
{\displaystyle G}
u
v
{\displaystyle uv}
u
{\displaystyle u}
v
{\displaystyle v}
P
G
=
P
G
−
u
v
−
P
G
/
u
v
{\displaystyle P_{G}=P_{G-uv}-P_{G/uv}}
즉, 이를 사용하여 색칠 다항식을 재귀적으로 계산할 수 있다.
임의의 그래프에 대하여
k
{\displaystyle k}
NP-완전 결정 문제 다. 이는 리처드 카프 가 1972년 에 보인 21개의 NP-완전 문제 중의 하나이다.
임의의 그래프
G
{\displaystyle G}
Δ
(
G
)
+
1
{\displaystyle \Delta (G)+1}
탐욕 알고리즘 으로 쉽게 찾을 수 있다.
그래프 색칠 문제는 컴파일러 에서 프로세서 레지스터 를 할당하는 문제, 무선 기지국 사이에서 간섭을 없애기 위한 주파수 할당 문제 등에 응용된다.
스도쿠 역시 일종의 그래프 색칠 문제이다. 이 경우, 9×9 격자의 각 행·각 열·각 3×3 부분격자는 클릭 을 이루며, 스도쿠는 주어진 부분적 9-색칠을 완성시키는 문제이다.