극점 (복소해석학)
(극 (복소해석학)에서 넘어옴)
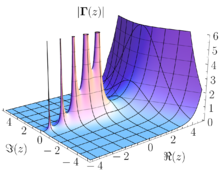
복소해석학에서 극점(極點, 영어: pole)은 국소적으로 가 에서 갖는 특이점과 같은 형태의 특이점이다.
정의
편집가 복소평면의 열린 부분집합이라고 하고, 정칙함수 가 주어졌다고 하자. 정수 에 대하여, 가 에서 제거 가능 특이점을 갖는지 여부를 생각할 수 있다. 즉 정칙함수 가 존재하여, 모든 에서 이게 될 수 있는지 여부이다. 만약 위 성질을 만족시키는 최소의 가 양의 정수라면, 가 에서 극점을 갖는다고 한다. 이 경우, 위 성질을 만족시키는 최소의 양의 정수 를 극점 의 계수(영어: order)라고 한다.
계수가 1인 극점을 단순극(單純極, 영어: simple pole)이라고 한다.
같이 보기
편집외부 링크
편집- Weisstein, Eric Wolfgang. “Pole”. 《Wolfram MathWorld》 (영어). Wolfram Research.

