단위구

수학에서 단위구는 고정된 중심점으로부터의 거리가 1인 점들의 집합이다. 일반화된 거리에 대한 개념이 사용된다; 닫힌 단위공은 고정된 중심점에서 거리가 1보다 작거나 같은 점들의 집합이다. 보통 특정한 점은 연구 중인 공간의 원점으로 구별되고 단위구 또는 단위공이 그 점을 중심으로 한다고 이해된다. 따라서 여기서는 항상 "그" 단위구나 "그" 단위공을 이야기 하는 것이다.

일부 1-구들. $\|{\boldsymbol {x}}\|_{2}$은 아래의 첫 번째 부분에서 이야기되는 유클리드 공간의 노름이다.

예를 들어, 원의 내부과 표면은 이차원 구이지만, 일차원 구는 그 "원"의 표면이다. 비슷하게, 일반적으로 "구"라고 부르는 유클리드 입체의 내부와 표면은 삼차원 구이지만, 이차원 구는 그 구의 표면이다.

단위구는 단순히 반지름이 1인 구이다. 단위구의 중요한 점은 어떤 구도 평행이동과 크기변환만으로 단위구로 변환될 수 있다는 것이다. 이 때문에 구의 특성은 일반적으로 단위구에 대한 연구로 줄일 수 있다.

유클리드 공간에서 단위구와 공

n차원 공간의 유클리드 공간에서, (n−1)차원 단위구는 다음 등식을 만족시키는 점들의 집합 $(x_{1},\ldots ,x_{n})$이다:

$x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}=1$

n차원 열린 단위 공은 다음 부등식을 만족시키는 점들의 집합이다:

$x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1$

그리고 n차원 닫힌 단위 공은 다음 부등식을 만족시키는 점들의 집합이다:

$x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\leq 1$

일반적인 넓이와 부피 공식

단위구의 고전적인 방정식은 반지름이 1이고 x-, y-, 또는 z-축의 교대가 없는 타원체의 방정식이다:

$f(x,y,z)=x^{2}+y^{2}+z^{2}=1$

n차원 유클리드 공간의 단위구의 부피와 표면적은 많은 해석학의 중요한 공식에 등장한다. n차원 단위공의 부피 V_n은 감마 함수를 사용해서 표현할 수 있다:

$V_{n}={\frac {\pi ^{n/2}}{\Gamma (1+n/2)}}={\begin{cases}{\pi ^{n/2}}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even,} \\~\\{\pi ^{\lfloor n/2\rfloor }2^{\lceil n/2\rceil }}/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}}$

이 때 n!!은 이중 팩토리얼이다.

(n−1)차원 단위구의 초부피 A_n(즉, n차원 단위공의 표면의 "넓이")은 다음과 같이 표현할 수 있다:

$A_{n}=nV_{n}={\frac {n\pi ^{n/2}}{\Gamma (1+n/2)}}={\frac {2\pi ^{n/2}}{\Gamma (n/2)}}\,,$

여기서 마지막 등식은 n > 0일 때만 성립한다.

일부 $n$값에 따른 표면적과 부피는 다음과 같다:

$n$	$A_{n}$ (표면적)		$V_{n}$ (부피)
0	$0(1/0!)\pi ^{0}$	0	$(1/0!)\pi ^{0}$	1
1	$1(2^{1}/1!!)\pi ^{0}$	2	$(2^{1}/1!!)\pi ^{0}$	2
2	$2(1/1!)\pi ^{1}=2\pi$	6.283	$(1/1!)\pi ^{1}=\pi$	3.141
3	$3(2^{2}/3!!)\pi ^{1}=4\pi$	12.57	$(2^{2}/3!!)\pi ^{1}=(4/3)\pi$	4.189
4	$4(1/2!)\pi ^{2}=2\pi ^{2}$	19.74	$(1/2!)\pi ^{2}=(1/2)\pi ^{2}$	4.935
5	$5(2^{3}/5!!)\pi ^{2}=(8/3)\pi ^{2}$	26.32	$(2^{3}/5!!)\pi ^{2}=(8/15)\pi ^{2}$	5.264
6	$6(1/3!)\pi ^{3}=\pi ^{3}$	31.01	$(1/3!)\pi ^{3}=(1/6)\pi ^{3}$	5.168
7	$7(2^{4}/7!!)\pi ^{3}=(16/15)\pi ^{3}$	33.07	$(2^{4}/7!!)\pi ^{3}=(16/105)\pi ^{3}$	4.725
8	$8(1/4!)\pi ^{4}=(1/3)\pi ^{4}$	32.47	$(1/4!)\pi ^{4}=(1/24)\pi ^{4}$	4.059
9	$9(2^{5}/9!!)\pi ^{4}=(32/105)\pi ^{4}$	29.69	$(2^{5}/9!!)\pi ^{4}=(32/945)\pi ^{4}$	3.299
10	$10(1/5!)\pi ^{5}=(1/12)\pi ^{5}$	25.50	$(1/5!)\pi ^{5}=(1/120)\pi ^{5}$	2.550

n ≥ 2일 때의 확장된 소숫점 아래는 표시된 정확도로 반올림되었다.

재귀

A_n값은 재귀를 만족시킨다:

$A_{0}=0$

$A_{1}=2$

$A_{2}=2\pi$

$A_{n}={\frac {2\pi }{n-2}}A_{n-2}$ for $n>2$.

V_n값도 재귀를 만족시킨다:

$V_{0}=1$

$V_{1}=2$

$V_{n}={\frac {2\pi }{n}}V_{n-2}$ for $n>1$.

분수 차원

 이 부분의 본문은 하우스도르프 측도입니다.

A_n과 V_n의 공식은 어떤 실수 n ≥ 0에 대해서도 계산할 수 있고, n이 음이아닌 정수일 때 구의 표면적과 공의 부피를 찾을 수 있는 적절한 환경이 있다.

이것은 (x–1)차원 구의 초부피(즉, x차원 단위공의 표면의 "넓이")를 x에 대한 연속 함수로 나타낸다.

이것은 x차원 공의 부피를 x에 대한 연속 함수로 나타낸다.

다른 반지름

 이 부분의 본문은 구입니다.

반지름이 r인 (n–1)차원 구의 표면적은 A_n rⁿ⁻¹이고, 반지름이 r인 n차원 공의 부피는 V_n rⁿ이다. 예를 들어, 반지름이 r인 삼차원 공의 표면적은 A = 4π r²이다. 반지름이 r인 삼차원 공의 부피는 V = 4π r³ / 3이다.

노름 벡터 공간의 단위공

더 정확하게, 노름이 $\|\cdot \|$의 노름 벡터 공간 $V$의 열린 단위구는 다음과 같다:

$\{x\in V:\|x\|<1\}$

이것은 (V,||·||)의 닫힌 단위공의 내부이다:

$\{x\in V:\|x\|\leq 1\}$

후자는 전자와 그 공통 경계인 단위구의 서로소 연합이고, (V,||·||)의 단위구는 다음과 같다:

$\{x\in V:\|x\|=1\}$

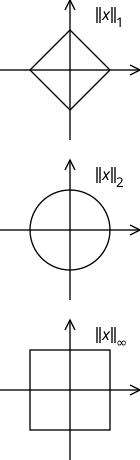
단위공의 '모양'은 전적으로 선택된 노름에 의존한다; 이것은 충분히 '모퉁이'를 가질 수도 있고, 예를 들면 Rⁿ의 노름 l_∞의 경우에는[−1,1]ⁿ처럼 보일 수도 있다. 둥근 공은 일상적인 유클리드 거리의 유한 차원의 경우에 기반하는 힐베르트 공간 노름으로 이해된다; 그 경계는 일반적으로 단위구를 의미하는 것이다. 여기에 다양한 값의 p에 대한 이차원 $\ell ^{p}$ 공간의 단위공의 그림을 그렸다 (단위공은 p < 1일 때는 오목하고 p ≥ 1일 때는 볼록하다):

모든 노름 공간의 단위공은 삼각 부등식에 의해서 반드시 볼록해야 하기 때문에 이것은 조건 p ≥ 1이 $\ell ^{p}$의 정의에 중요한지 보여준다.

이 이차원 단위공의 지름 $C_{p}$에 대해서 주목하라:

$C_{0}=C_{\infty }=8$은 최대값이다.

$C_{1}=4{\sqrt {2}}$은 최솟값이다.

$C_{2}=2\pi \,.$

일반화

측도 공간

위의 세 정의 모두는 선택한 원점에 대하여 직접적으로 거리 공간으로 일반화 된다. 하지만, 위상적 고려사항(내부, 닫힘, 경계)은 같은 방법으로 적용될 필요는 없다(예를 들면, 초거리 공간에서, 이 세 개 전부는 열려있는 동시에 닫힌 집합이다). 그리고 심지어 단위구는 어떤 거리 공간에서 빌 수도 있다.

이차 형식

V가 실이차 형식 F:V → R을 가지는 선형 공간이면 { p ∈ V : F(p) = 1 }은 단위구또는 V의 단위 준-구 로 부를 수 도 있다. 예를 들어, 이차 형식 $x^{2}-y^{2}$에 대해서 집합이 1과 같을 때, 분할복소수평면에서 "단위원"과 같은 역할을 하는 단위 쌍곡선을 만들어낸다. 비슷하게, 이차 형식 x²는 쌍대수평면의 단위 구인 선의 쌍을 얻는다.

같이 보기

• 공
• 초구
• 구 (기하학)
• 초타원
• 단위원
• 단위 디스크
• 단위구 묶음
• 단위정사각형
• 단위정육면체

각주

• Mahlon M. Day (1958) Normed Linear Spaces, page 24, Springer-Verlag.
• Deza, E.; Deza, M. (2006), 《Dictionary of Distances》, Elsevier, ISBN 0-444-52087-2 . Reviewed in Newsletter of the European Mathematical Society 64 (June 2007), p. 57. This book is organized as a list of distances of many types, each with a brief description.

외부 링크

• Weisstein, Eric Wolfgang. “Unit sphere”. 《Wolfram MathWorld》 (영어). Wolfram Research.