확률론 에서 마팅게일 (영어 : martingale 마턴게일[* ] , 프랑스어 : martingale 마르탱갈[* ] )은 확률 과정 의 하나로, 과거의 모든 정보를 알고 있다면 미래의 기댓값 이 현재 값과 동일한 과정이다.[ 1]
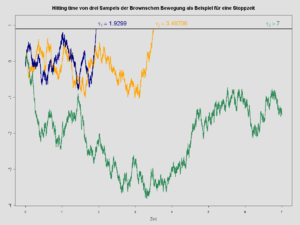
변수가 어떤 상계에 이르면 멈추게 되는 1차원 브라운 운동 은 마팅게일의 한 예이다. 이는 돈이 다 떨어지면 파산하게 되는 도박꾼을 나타내는 확률론적 모형이다.
다음이 주어졌다고 하자.
전순서 집합
(
T
,
≤
)
{\displaystyle (T,\leq )}
여과 확률 공간
(
Ω
,
F
t
,
Pr
)
t
∈
T
{\displaystyle (\Omega ,{\mathcal {F}}_{t},\Pr )_{t\in T}}
유클리드 공간
R
d
{\displaystyle \mathbb {R} ^{d}}
보렐 가측 공간 으로 가정한다. (르베그 시그마 대수 가 아니다.)그렇다면,
(
Ω
,
F
t
,
Pr
)
t
∈
T
∪
{
∞
}
{\displaystyle (\Omega ,{\mathcal {F}}_{t},\Pr )_{t\in T\cup \{\infty \}}}
순응 확률 과정
(
X
t
:
Ω
→
)
t
∈
T
{\displaystyle (X_{t}\colon \Omega \to )_{t\in T}}
마팅게일 이라고 한다.
(기댓값 의 존재) 임의의
t
∈
T
{\displaystyle t\in T}
E
(
‖
X
t
‖
)
<
∞
{\displaystyle \operatorname {E} (\|X_{t}\|)<\infty }
X
t
∈
L
1
(
Ω
;
R
d
)
{\displaystyle X_{t}\in \operatorname {L} ^{1}(\Omega ;\mathbb {R} ^{d})}
(마팅게일 성질) 임의의
s
,
t
∈
T
{\displaystyle s,t\in T}
s
≤
t
{\displaystyle s\leq t}
E
(
X
s
|
F
s
)
=
E
(
X
t
|
F
s
)
:
F
s
→
R
d
{\displaystyle \mathbb {E} (X_{s}|{\mathcal {F}}_{s})=\mathbb {E} (X_{t}|{\mathcal {F}}_{s})\colon {\mathcal {F}}_{s}\to \mathbb {R} ^{d}}
A
∈
Σ
s
{\displaystyle A\in \Sigma _{s}}
E
(
X
t
|
A
)
=
E
(
X
s
|
A
)
∈
R
d
{\displaystyle \mathbb {E} (X_{t}|A)=\mathbb {E} (X_{s}|A)\in \mathbb {R} ^{d}}
1
A
:
Ω
→
R
{\displaystyle 1_{A}\colon \Omega \to \mathbb {R} }
A
{\displaystyle A}
지시 함수 이다.
물론, 이 정의에서
s
=
t
{\displaystyle s=t}
여기서
E
(
−
|
−
)
{\displaystyle \mathbb {E} (-|-)}
조건부 기댓값 을 뜻한다.
마팅게일의 정의의 둘째 조건은 다음과 같이 풀어 해석할 수 있다.
현재
s
{\displaystyle s}
A
∈
F
s
{\displaystyle A\in {\mathcal {F}}_{s}}
t
≥
s
{\displaystyle t\geq s}
X
{\displaystyle X}
X
t
{\displaystyle X_{t}}
E
(
X
t
|
A
)
{\displaystyle \mathbb {E} (X_{t}|A)}
E
(
X
s
|
A
)
{\displaystyle \operatorname {E} (X_{s}|A)}
d
=
1
{\displaystyle d=1}
열마팅게일 (劣martingale, 영어 : submartingale 서브마팅게일[* ] )의 개념을 얻는다.
(열마팅게일 조건) 임의의
s
,
t
∈
T
{\displaystyle s,t\in T}
s
≤
t
{\displaystyle s\leq t}
E
(
X
s
|
F
s
)
≤
E
(
X
t
|
F
s
)
:
F
s
→
R
d
{\displaystyle \mathbb {E} (X_{s}|{\mathcal {F}}_{s})\leq \mathbb {E} (X_{t}|{\mathcal {F}}_{s})\colon {\mathcal {F}}_{s}\to \mathbb {R} ^{d}}
마찬가지로, 마팅게일의 정의에서, 둘째 조건을 다음과 같이 대체할 경우, 우마팅게일 (優martingale, 영어 : supermartingale 슈퍼마팅게일[* ] )은 의 개념을 얻는다.
(우마팅게일 조건) 임의의
s
,
t
∈
T
{\displaystyle s,t\in T}
s
≤
t
{\displaystyle s\leq t}
E
(
X
s
|
F
s
)
≥
E
(
X
t
|
F
s
)
:
F
s
→
R
d
{\displaystyle \mathbb {E} (X_{s}|{\mathcal {F}}_{s})\geq \mathbb {E} (X_{t}|{\mathcal {F}}_{s})\colon {\mathcal {F}}_{s}\to \mathbb {R} ^{d}}
만약
(
X
t
)
t
∈
T
{\displaystyle (X_{t})_{t\in \mathbb {T} }}
(
−
X
t
)
t
∈
T
{\displaystyle (-X_{t})_{t\in T}}
확률 과정 은 마팅게일이다.
다음과 같은 특별한 경우를 생각하자.
(
Ω
,
F
t
,
Pr
)
{\displaystyle (\Omega ,{\mathcal {F}}_{t},\Pr )}
(
Y
t
:
Ω
→
R
d
)
t
∈
T
{\displaystyle (Y_{t}\colon \Omega \to \mathbb {R} ^{d})_{t\in T}}
자연 여과 확률 공간 이다.그렇다면, 마팅게일의 정의의 둘째 조건은 다음과 같이 나타내어진다.
E
(
X
t
|
{
Y
r
}
r
≤
s
)
=
E
(
X
s
|
{
Y
r
}
r
≤
s
)
{\displaystyle \mathbb {E} (X_{t}|\{Y_{r}\}_{r\leq s})=\mathbb {E} (X_{s}|\{Y_{r}\}_{r\leq s})}
특히,
X
=
Y
{\displaystyle X=Y}
예를 들어,
T
=
N
=
{
0
,
1
,
2
,
…
}
{\displaystyle T=\mathbb {N} =\{0,1,2,\dotsc \}}
자연수 집합)인 경우를 생각하자. 이는 이산 시간 확률 과정 에 해당한다. 이 경우,
(
X
t
:
Ω
→
R
d
)
t
∈
Z
{\displaystyle (X_{t}\colon \Omega \to \mathbb {R} ^{d})_{t\in \mathbb {Z} }}
(기댓값의 존재) 임의의
t
∈
N
{\displaystyle t\in \mathbb {N} }
E
(
‖
X
t
‖
)
<
∞
{\displaystyle \mathbb {E} (\|X_{t}\|)<\infty }
(마팅게일 성질)
E
(
X
s
+
1
|
X
0
,
X
1
,
…
,
X
s
)
=
E
(
X
s
)
{\displaystyle \mathbb {E} (X_{s+1}|X_{0},X_{1},\dotsc ,X_{s})=\operatorname {E} (X_{s})}
이 조건은
t
=
s
+
1
{\displaystyle t=s+1}
E
(
X
s
+
2
|
X
0
,
…
,
X
s
)
=
E
(
X
s
+
2
|
X
0
,
…
,
X
s
,
X
s
+
1
)
↾
F
s
=
E
(
X
s
+
1
|
X
0
,
…
,
X
s
,
X
s
+
1
)
↾
F
s
=
E
(
X
s
+
1
|
X
0
,
…
,
X
s
)
=
E
(
X
s
)
{\displaystyle \mathbb {E} (X_{s+2}|X_{0},\dotsc ,X_{s})=\mathbb {E} (X_{s+2}|X_{0},\dotsc ,X_{s},X_{s+1})\upharpoonright {\mathcal {F}}_{s}=\mathbb {E} (X_{s+1}|X_{0},\dotsc ,X_{s},X_{s+1})\upharpoonright {\mathcal {F}}_{s}=\mathbb {E} (X_{s+1}|X_{0},\dotsc ,X_{s})=\mathbb {E} (X_{s})}
와 같이 수학적 귀납법 으로 모든
t
≥
s
{\displaystyle t\geq s}
F
s
{\displaystyle {\mathcal {F}}_{s}}
X
{\displaystyle X}
자연 여과 확률 공간 이다.
마팅게일(프랑스어 : martingale 마르탱갈[* ] )이라는 단어는 프랑스 남부의 지명 마르티그 에서 유래한다.[ 2] [ 2] :§2 거의 확실하게 이기는 순간이 오기 때문에 언젠가는 돈을 딸 수 있지만, 실제로는 재산이 유한하기 때문에 돈을 따기 전에 가진 돈을 잃을 확률이 존재하게 된다. ‘마르탱갈’이라는 단어는 이 전략의 어리석음을 마르티그 지방 사람들의 (파리 사람들의 편견에 따르면) 어리숙하고 순진함에 빗댄 것이다.[ 2] :108, §4
폴 피에르 레비 (프랑스어 : Paul Pierre Lévy )가 처음으로 확률론 에 이 마팅게일 전략을 도입하였으며, 조지프 두브 역시 마팅게일의 이론적 발전에 크게 기여하였다. 확률론에 마팅게일이 도입된 이유 중의 하나는 마팅게일 전략으로 도박을 통해 수익을 얻는 것이 불가능하다는 것을 증명하고자 하는 데 있었다.
↑ Williams, David (1991). 《Probability with martingales》 (영어). Cambridge University Press. ISBN 0-521-40605-6 ↑ 가 나 다 Mansuy, Roger (2005). “Histoire de martingales”. 《Mathématiques & Sciences Humaines / Mathematical Social Sciences》 (프랑스어) 169 . doi :10.4000/msh.2945 . ISSN 0987-6936 .