띠구조
응집물질물리학에서 띠구조(-構造, band structure)는 결정 속 전자의 분산 관계이다. 파수-에너지 공간에서 여러 개의 곡선으로 이루어지며, 각 곡선을 결정의 에너지 띠(energy band)라고 한다. 띠구조를 다루는 이론을 띠 이론(band theory)이라고 한다.
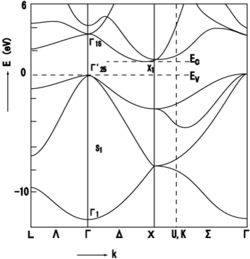
정의
편집결정 속에는 이온 껍질에 의한 주기적인 전기장이 존재하며, 이에 따라 결정 속에 전자가 가질 수 있는 에너지가 제한된다. 결정 속 전자가 존재할 수 있는 에너지 영역을 에너지 띠라고 부르고, 전자가 취할 수 없는 에너지 영역을 띠틈이라고 부른다. 에너지 띠에 어떻게 전자가 배치되어 있느냐에 따라서 그 고체의 전기전도성이나 광학적 특성이 결정된다.
블로흐 정리에 따라서, 결정 속 전자의 파동 함수(전자 상태)는 그 파수 에 의하여 결정된다. 이것이 에너지와 파수의 관계식을 원리적으로 기술할 수 있는 것을 보장하고 있다. 여기서 말하는 파수는 결정구조의 병진 대칭성때문에 나타나는 양자수이며 실재 입자의 운동량으로 해석할 수 없다. 결정 구조 속의 전자 상태 함수를 기술하기 위해 주기적 경계 조건을 사용하면 이 파수 벡터들은 소위 브릴루앙 영역 안에 모두 들어옴을 보일 수 있다. 따라서 브릴루앙 영역의 파수들에 대응하여 에너지 준위들을 그릴 수 있는데 이를 전자의 띠구조라고 한다. 일반적으론 브릴루앙 영역에서, 대칭성이 좋은 특정한 파수들을 잇는 선을 따라 에너지 띠를 그린다. 각 파수마다 전자가 있을 수 있는 특정 에너지들이 있는데, 이것들이 연결되어 곡선을 이룬다.
띠구조를 보는 것으로 띠틈이 비어있는지 아닌지 (즉 대응하는 계가 금속인가 아닌가), 띠분산이 강한가 약한가처럼 밤전자상태의 차이 (분산이 약하면, 즉 띠의 폭이 좁으면 그 띠의 전자는 보다 속박된 상태가 된다. 강하면 반대임), 다른 계끼리의 띠구조를 비교하여 계의 안정성을 논의할 수 있다. (다만, 띠구조만으로 판단할 수 없는 경우도 있다.)
그리고 결정 구조에 대한 병진 대칭성의 영향으로부터 띠틈이 생기는 경우도 있다.
도체·절연체·반도체의 띠구조
편집금속과 다른 도체에서는 적어도 하나의 에너지 띠가 페르미면을 횡단한다.
대부분의 반도체나 절연체의 띠구조는 파수 공간을 무시하고 띠틈 주변만 고려하여 근사할 수 있다. 절연체와 반도체에서 에너지 띠는 원자가띠와 전도띠로 나뉘어 페르미 준위는 띠틈 속에 존재한다.
다만, 띠 이론은 근본적으로는 일체문제에 의한 접근법이므로, 전자 사이의 상호작용이 약한 물질에서 잘 맞는다. 따라서 띠 이론은 전자들 사이의 강한 상호작용에 의한 절연 상태인 모트 절연체(Mott insulator)를 금속으로 잘못 예측하는 경우가 있다. 따라서 뭇입자계를 다루는 강상관 전자계(strongly correlated electron system)로 불리는 분야가 별도로 존재한다.
계산
편집띠구조를 이론적으로 계산하려면 여러 방법이 있다. 이들은 경험적인 것부터 비경험적(제일원리적)인 것까지 다양하다. 이들은 보통 결정과 같은 고체를 다루지만, 표면계나 액체를 다루는 계산법도 있다.
대표적인 수법으로 유사퍼텐셜 + 평면파 기저에 의하여 APW, KKR와 같은 전전자 수법, 제일원리 분자역동학법, 밀접 결합 근사법 등이 있다. 제일원리 분자역동학 수법에서 전자 상태와 함께 대상이 되는 계의 구조 최적화, 즉 안정 구조를 요구할 수 있다.
띠 계산은 원래 결정같은 주기적 경계조건이 존재하는 계가 계산 대상이었지만 그 후에 표면계나 불규칙 이원합금같은 비주기계에 대해서도 계산이 이루어지게 되었다. 표면계에 관해서는 슬래브 근사(영어: slab approxmation)를 이용해 계산하는 것이 가장 표준적이다. 불원칙 이원합금같은, 퍼텐셜이 무작위한 계에는 간접성 퍼텐셜 근사(coherent potential approximation)가 이용되는 것이 많다. 또한 실공간법과 같은, 경계 조건에 묶이지 않는 계산 방법도 출현하고 있다.
같이 보기
편집각주
편집- ↑ James R. Chelikowsky, Marvin L. Cohen (1974년 12월). “Electronic structure of silicon”. 《Physical Review B》 10 (12): 5095–5107. doi:10.1103/PhysRevB.10.5095.
- Kittel, Charles (1996). 《Introduction to solid state physics》 (영어). New York: Wiley. ISBN 0-471-14286-7.
- Ashcroft, Neil W.; N. David Mermin (1976). 《Solid state physics》 (영어). Orlando: Harcourt. ISBN 0-03-049346-3.
외부 링크
편집- (일본어) 小林一昭. “バンド計算入門”.
- 정기수. “고체의 에너지띠”.[깨진 링크(과거 내용 찾기)]