벨먼-포드 알고리즘

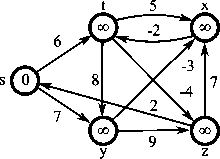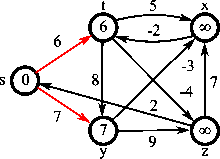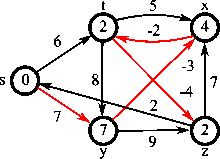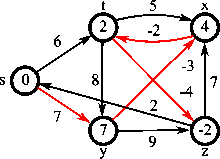
벨먼-포드 알고리즘(영어: Bellman-Ford algorithm)은 가중 유향 그래프에서 최단 경로 문제를 푸는 알고리즘이다. 이때 변의 가중치는 음수일 수도 있다. 데이크스트라 알고리즘은 벨먼-포드 알고리즘과 동일한 작업을 수행하고 실행속도도 더 빠르다. 하지만 다익스트라 알고리즘은 가중치가 음수인 경우는 처리할 수 없으므로, 이런 경우에는 벨먼-포드 알고리즘을 사용한다.

벨먼-포드 알고리즘

분류	최단 경로 문제
자료 구조	그래프
최악 시간복잡도	$\Theta (|V||E|)$
최선 시간복잡도	$\Theta (|E|)$
공간복잡도	$\Theta (|V|)$

V와 E가 각각 그래프에서 꼭짓점과 변의 개수라고 한다면, 벨먼-포드 알고리즘의 실행시간은 $\Theta (|V||E|)$이다.

의사코드 (Pseudo-code)

 // 그래프의 자료구조 정의
record vertex {
    list edges
    real distance
    vertex predecessor
}
record edge {
    node source
    node destination
    real weight
}

function BellmanFord(list vertices, list edges, vertex source)
   // This implementation takes in a graph, represented as lists of vertices
   // and edges, and modifies the vertices so that their distance and
   // predecessor attributes store the shortest paths.

   // Step 1:  그래프 초기화
   for each vertex v in vertices:
       if v is source then v.distance = 0
       else v.distance := infinity
       v.predecessor := null

   // Step 2: 이완 작업 반복
   for i from 1 to size(vertices):
       for each edge uv in edges:
           u := uv.source
           v := uv.destination             // uv is the edge from u to v
           if v.distance > u.distance + uv.weight
               v.distance := u.distance + uv.weight
               v.predecessor := u

   // Step 3: 
   for each edge uv in edges:
       u := uv.source
       v := uv.destination
       if v.distance > u.distance + uv.weight
           error "Graph contains a negative-weight cycle"

실제 프로그래밍 언어로 구현한 소스 코드

C

#define INFINITY ((1 << (sizeof(int)*8-2))-1)

typedef struct
{
	int source;
	int dest;
	int weight;
}Edge;

void BellmanFord(Edge edges[], int edgecount, int nodecount, int source)
{
	int i,j ;
	int* distance = malloc(nodecount*sizeof(int));
	for(i = 0; i < nodecount; i++)
	{
		if(i == source) distance[i] = 0;
		else distance[i] = INFINITY;
	}
	for(i = 0; i < nodecount; i++)
	{
		for(j = 0; j < edgecount; j++)
		{
			/*
			 * Note that INFINITY is actually a finite number in this code, so because of overflow
			 * "distance[edges[j].source] + edges[j].weight" can be a very small number,
			 * in fact smaller than "distance[edges[j].dest]".
			 *
			 * One solution is to skip the following if-statement,
			 * if "distance[edges[j].source]" == INFINITY
			 */
			if(distance[edges[j].dest] > distance[edges[j].source] + edges[j].weight)
			{
				distance[edges[j].dest] = distance[edges[j].source] + edges[j].weight;
			}
		}
	}
	for(i = 0; i < edgecount; i++)
	{
		if(distance[edges[i].dest] > distance[edges[i].source] + edges[i].weight)
		{
			printf("Error occurred. Negative edge weight cycles detected");
			break;
		}
	}
	for(i = 0; i < nodecount; i++)
	{
		printf("The shortest distance between nodes %i and %i is %i\n", source, i, distance[i]);
	}
}

참고 문헌

• Richard Bellman: On a Routing Problem, in Quarterly of Applied Mathematics, 16(1), pp.87-90, 1958.
• Lestor R. Ford jr., D. R. Fulkerson: Flows in Networks, Princeton University Press, 1962.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 24.1: The Bellman-Ford algorithm, pp.588–592.