부채꼴
원에서 두 개의 반지름과 하나의 호로 둘러싸인 영역
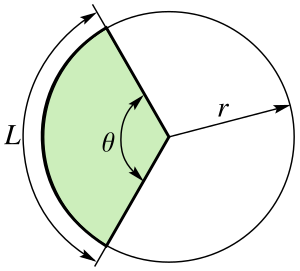
부채꼴(circular sector)은 원에서 두 개의 반지름과 하나의 호로 둘러싸인 영역이다. 선상(扇狀)이라고도 한다. 중심각이 180˚인 부채꼴을 반원이라고 부르며, 원은 중심각이 360˚인 부채꼴이라고 생각할 수 있다.
공식
편집호의 길이
편집부채꼴의 호의 길이는 라디안의 정의를 이용하여 구할 수 있다. 1라디안은 반지름과 호의 길이가 같을 때의 각의 크기이므로 호의 길이는 반지름과 각의 곱으로 표현할 수 있다.
전체 둘레
편집부채꼴의 둘레는 부채꼴 호의 길이 + 반지름 2개 이므로, 아래와 같이 표현할 수 있다.
넓이
편집부채꼴의 넓이는 다음과 같이 계산할 수 있다.
중심각을 , 원의 반지름을 로 두자. 그러면 원의 넓이는 이다. 부채꼴의 넓이는 원의 넓이에 중심각의 크기와 의 비를 곱하면 구할 수 있다. 부채꼴의 넓이는 중심각의 크기에 비례하고, 원 전체의 중심각 크기는 이기 때문이다.
여기에 를 대입하면
그리고 만약 가 도(°) 단위로 주어졌다면 다음과 같은 식이 얻어진다.
성질
편집부채꼴의 양쪽 면을 서로 연결하여 붙이면 원뿔이다. 이때 부채꼴의 호는 원뿔의 밑면의 원의 둘레가 된다.
- 부채꼴의 넓이(원뿔의 옆넓이 면적)
같이 보기
편집| 이 글은 수학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |