오일러 직선

기하학에서 오일러 직선(Euler直線, 영어: Euler line)은 정삼각형이 아닌 삼각형의 외심, 무게 중심, 구점원의 중심, 수심을 지나는 직선이다. 정삼각형에서는 이 네 중심이 일치하기 때문에 오일러 직선이 정의되지 않는다.

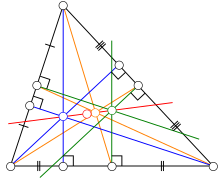
오일러선 (붉은색)은 무게중심 (주황색), 수심 (푸른색), 외심 (초록색)과 구점원의 중심 (붉은색)을 한 직선으로 이어준다.

정의

삼각형 $ABC$ 의 외심 $O$ , 무게 중심 $G$ , 구점원의 중심 $N$ , 수심 $H$ 는 공선점을 이룬다. 특히 삼각형 $ABC$ 가 정삼각형이 아닐 경우 이들을 모두 지나는 직선은 유일하게 존재한다. 이 직선을 삼각형 $ABC$ 의 오일러 직선이라고 한다. 삼각형 $ABC$ 가 정삼각형일 경우 이 네 점은 모두 일치하므로, 이들을 모두 지나는 직선은 무한히 많으며, 이 경우 오일러 직선은 정의되지 않는다.

나겔 직선

삼각형 $ABC$ 의 내심 $I$ , 무게 중심 $G$ , 슈피커 중심 $S$ , 나겔 점 $N'$ 은 공선점을 이룬다. 특히 삼각형 $ABC$ 가 정삼각형이 아닐 경우 이들을 모두 지나는 직선은 유일하게 존재한다. 이 직선을 삼각형 $ABC$ 의 나겔 직선(Nagel直線, 영어: Nagel line)이라고 한다. 삼각형 $ABC$ 가 정삼각형일 경우 이 네 점은 모두 일치하므로, 이들을 모두 지나는 직선은 무한히 많으며, 이 경우 나겔 직선은 정의되지 않는다.

성질

오일러 직선 위의 점

정삼각형이 아닌 삼각형 $ABC$ 의 다음과 같은 점들은 오일러 직선 위의 점이다.

외심 $O$ : 외접원의 중심이자, 각 변의 수직 이등분선의 교점
무게 중심 $G$ : 세 중선의 교점
구점원의 중심 $N$ : 각 변의 중점, 각 꼭짓점에서 대변에 내린 수선의 발, 각 꼭짓점과 수심 사이의 선분의 중점을 지나는 원의 중심
수심 $H$ : 각 꼭짓점에서 대변에 내린 수선의 교점

오일러 직선 위의 점 사이의 위치 관계

(정삼각형일 수 있는) 삼각형의 무게 중심은 외심과 수심을 잇는 선분의 (외심에 더 가까운) 삼등분점이며, 구점원의 중심은 이 선분의 중점이다. 즉, 삼각형 $ABC$ 의 외심, 무게 중심, 구점원의 중심, 수심을 각각 $O$ , $G$ , $N$ , $H$ 라고 할 경우

{\overrightarrow {OH}}=3{\overrightarrow {OG}}=2{\overrightarrow {ON}}=6{\overrightarrow {GN}}

이다.^[1]^{:7, §1.3}

나겔 직선 위의 점

정삼각형이 아닌 삼각형 $ABC$ 의 다음과 같은 점들은 나겔 직선 위의 점이다.

내심 $I$ : 내접원의 중심이자, 세 각의 이등분선의 교점
무게 중심 $G$ :삼각형과 한 꼭짓점과 대변의 중점을 이은 중선들의 교점
슈피커 중심 $S$ : 중점 삼각형의 내심
나겔 점 $N'$ : 각 꼭짓점과 대변 위 방접원의 접점을 잇는 선분의 교점

나겔 직선 위의 점 사이의 위치 관계

(정삼각형일 수 있는) 삼각형의 무게 중심은 내심과 나겔 점을 잇는 선분의 (내심에 더 가까운) 삼등분점이며, 슈피커 중심은 이 선분의 중점이다. 즉, 삼각형 $ABC$ 의 내심, 무게 중심, 슈피커 중심, 나겔 점을 각각 $I$ , $G$ , $S$ , $N'$ 이라고 할 경우

{\overrightarrow {IN'}}=3{\overrightarrow {IG}}=2{\overrightarrow {IS}}=6{\overrightarrow {GS}}

이다.^[1]^{:7, §1.4}

각주

↑ ^가 ^나 Honsberger, Ross (1995). 《Episodes in Nineteenth and Twentieth Century Euclidean Geometry》. New Mathematical Library (영어) 37. Washington: The Mathematical Association of America. ISBN 0-88385-639-5.

외부 링크

“Euler straight line”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
Weisstein, Eric Wolfgang. “Euler line”. 《Wolfram MathWorld》 (영어). Wolfram Research.
Weisstein, Eric Wolfgang. “Nagel line”. 《Wolfram MathWorld》 (영어). Wolfram Research.

[Honsberger-1] 가 ^나 Honsberger, Ross (1995). 《Episodes in Nineteenth and Twentieth Century Euclidean Geometry》. New Mathematical Library (영어) 37. Washington: The Mathematical Association of America. ISBN 0-88385-639-5.

[1]