외접 사각형
외접 사각형(영어: tangential quadrilateral)은 사각형의 네 변이 모두 한 원에 접하는 사각형이다.
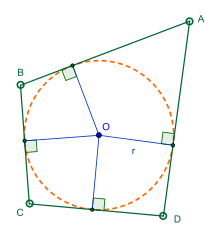
즉, 외접 사각형이란 내접원을 가지는 사각형을 말한다. 모든 삼각형은 내접원을 가지지만, 사각형에 대해서는 이가 성립하지 않는다. 예를 들어, 마름모는 내접원을 가지지만, 정사각형이 아닌 직사각형은 내접원이 존재하지 않는다.
성질
편집피토 정리에 의해, 마주보는 각변의 길이의 합이 같다. 즉, 이며, 임의의 볼록사각형에 대해 위가 성립하면 그 사각형은 외접 사각형이다.
외접사각형의 넓이는 다음과 같이 구할 수 있다.
사각형의 넓이를 , 각 변의 길이를 , 내접원의 반지름을 이라 할 때 이에 의해 항상 이며, 넓이는 내접사각형일 때 최대이다.
참조
편집- ↑ Pritsker, Boris (2017년 9월 13일). 《Geometrical Kaleidoscope》 (영어). Courier Dover Publications. ISBN 978-0-486-81241-0.