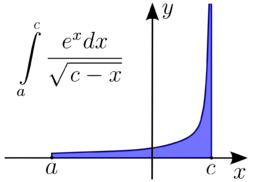
실수 구간에 정의된 실숫값 함수
f
:
[
a
,
b
]
∖
{
−
∞
,
∞
}
→
R
(
−
∞
≤
a
<
b
≤
∞
)
{\displaystyle f\colon [a,b]\setminus \{-\infty ,\infty \}\to \mathbb {R} \qquad (-\infty \leq a<b\leq \infty )}
에 대하여, 다음을 만족시키는
n
∈
N
{\displaystyle n\in \mathbb {N} }
a
=
c
0
<
c
1
<
⋯
<
c
n
=
b
{\displaystyle a=c_{0}<c_{1}<\cdots <c_{n}=b}
임의의
k
=
1
,
2
,
…
,
n
{\displaystyle k=1,2,\dots ,n}
[
γ
k
,
δ
k
]
⊆
(
c
k
−
1
,
c
k
)
{\displaystyle [\gamma _{k},\delta _{k}]\subseteq (c_{k-1},c_{k})}
∫
γ
k
δ
k
f
(
x
)
d
x
∈
R
{\displaystyle \int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x\in \mathbb {R} }
그렇다면,
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
b
f
(
x
)
d
x
=
lim
γ
1
→
c
0
+
0
lim
δ
1
→
c
1
−
0
⋯
lim
γ
n
→
c
n
−
1
+
0
lim
δ
n
→
c
n
−
0
∑
k
=
1
n
∫
γ
k
δ
k
f
(
x
)
d
x
=
∑
k
=
1
n
(
lim
γ
k
→
c
k
−
1
+
0
∫
γ
k
x
k
−
1
+
x
k
2
f
(
x
)
d
x
+
lim
δ
k
→
c
k
−
0
∫
x
k
−
1
+
x
k
2
δ
k
f
(
x
)
d
x
)
{\displaystyle {\begin{aligned}\int _{a}^{b}f(x)\mathrm {d} x&=\lim _{\gamma _{1}\to c_{0}+0}\lim _{\delta _{1}\to c_{1}-0}\cdots \lim _{\gamma _{n}\to c_{n-1}+0}\lim _{\delta _{n}\to c_{n}-0}\sum _{k=1}^{n}\int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x\\&=\sum _{k=1}^{n}\left(\lim _{\gamma _{k}\to c_{k-1}+0}\int _{\gamma _{k}}^{\frac {x_{k-1}+x_{k}}{2}}f(x)\mathrm {d} x+\lim _{\delta _{k}\to c_{k}-0}\int _{\frac {x_{k-1}+x_{k}}{2}}^{\delta _{k}}f(x)\mathrm {d} x\right)\end{aligned}}}
물론 이상 적분은 존재하지 않을 수 있다. 존재한다면, 이상 적분이 수렴 (收斂)한다고 하며, 존재하지 않는다면, 이상적분이 발산 (發散)한다고 한다. 함수의 절댓값 의 이상 적분
∫
a
b
|
f
(
x
)
|
d
x
{\displaystyle \int _{a}^{b}|f(x)|\mathrm {d} x}
의 수렴은 원래 이상 적분의 수렴보다 더 강한 조건이다. 절댓값의 이상 적분이 수렴한다면, 원래 이상 적분이 절대 수렴 (絶對收斂)한다고 한다. 수렴하지만 절대 수렴하지 않는 이상 적분을 조건 수렴 (條件收斂)한다고 한다.
특히, 실수 함수
f
:
[
a
,
b
)
→
R
(
−
∞
<
a
<
b
≤
∞
)
{\displaystyle f\colon [a,b)\to \mathbb {R} \qquad (-\infty <a<b\leq \infty )}
[
a
,
β
]
⊆
[
a
,
b
)
{\displaystyle [a,\beta ]\subseteq [a,b)}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
b
f
(
x
)
d
x
=
lim
β
→
b
−
0
∫
a
β
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\beta \to b-0}\int _{a}^{\beta }f(x)\mathrm {d} x}
마찬가지로, 실수 함수
f
:
(
a
,
b
]
→
R
(
−
∞
≤
a
<
b
<
∞
)
{\displaystyle f\colon (a,b]\to \mathbb {R} \qquad (-\infty \leq a<b<\infty )}
[
α
,
b
]
⊆
(
a
,
b
]
{\displaystyle [\alpha ,b]\subseteq (a,b]}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
b
f
(
x
)
d
x
=
lim
α
→
a
+
0
∫
α
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\int _{\alpha }^{b}f(x)\mathrm {d} x}
또한, 실수 함수
f
:
(
a
,
b
)
→
R
(
−
∞
≤
a
<
b
≤
∞
)
{\displaystyle f\colon (a,b)\to \mathbb {R} \qquad (-\infty \leq a<b\leq \infty )}
[
α
,
β
]
⊆
(
a
,
b
)
{\displaystyle [\alpha ,\beta ]\subseteq (a,b)}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
b
f
(
x
)
d
x
=
lim
α
→
a
+
0
lim
β
→
b
−
0
∫
α
β
f
(
x
)
d
x
=
lim
α
→
a
+
0
∫
α
a
+
b
2
f
(
x
)
d
x
+
lim
β
→
b
−
0
∫
a
+
b
2
β
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\lim _{\beta \to b-0}\int _{\alpha }^{\beta }f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\int _{\alpha }^{\frac {a+b}{2}}f(x)\mathrm {d} x+\lim _{\beta \to b-0}\int _{\frac {a+b}{2}}^{\beta }f(x)\mathrm {d} x}
또한, 실수 함수
f
:
[
a
,
b
]
→
R
(
−
∞
<
a
<
c
<
b
<
∞
)
{\displaystyle f\colon [a,b]\to \mathbb {R} \qquad (-\infty <a<c<b<\infty )}
[
a
,
δ
]
⊆
[
a
,
c
)
{\displaystyle [a,\delta ]\subseteq [a,c)}
[
γ
,
b
]
⊆
(
c
,
b
]
{\displaystyle [\gamma ,b]\subseteq (c,b]}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
b
f
(
x
)
d
x
=
lim
δ
→
c
−
0
lim
γ
→
c
+
0
(
∫
a
δ
f
(
x
)
d
x
+
∫
γ
b
f
(
x
)
d
x
)
=
lim
δ
→
c
−
0
∫
a
δ
f
(
x
)
d
x
+
lim
γ
→
c
+
0
∫
γ
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\delta \to c-0}\lim _{\gamma \to c+0}\left(\int _{a}^{\delta }f(x)\mathrm {d} x+\int _{\gamma }^{b}f(x)\mathrm {d} x\right)=\lim _{\delta \to c-0}\int _{a}^{\delta }f(x)\mathrm {d} x+\lim _{\gamma \to c+0}\int _{\gamma }^{b}f(x)\mathrm {d} x}
위와 같은 여러 경우에, 만약 피적분 함수가 직접 적분하지 못하는 곳의 임의의 근방에서 무계 함수 라면, 그 이상 적분을 특이 적분 (特異積分, 영어 : singular integral )이라고 한다.
특히, 실수 함수
f
:
[
a
,
∞
)
→
R
(
a
∈
R
)
{\displaystyle f\colon [a,\infty )\to \mathbb {R} \qquad (a\in \mathbb {R} )}
[
a
,
β
]
⊆
[
a
,
∞
)
{\displaystyle [a,\beta ]\subseteq [a,\infty )}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
a
∞
f
(
x
)
d
x
=
lim
β
→
∞
∫
a
β
f
(
x
)
d
x
{\displaystyle \int _{a}^{\infty }f(x)\mathrm {d} x=\lim _{\beta \to \infty }\int _{a}^{\beta }f(x)\mathrm {d} x}
마찬가지로, 실수 함수
f
:
(
−
∞
,
b
]
→
R
(
b
∈
R
)
{\displaystyle f\colon (-\infty ,b]\to \mathbb {R} \qquad (b\in \mathbb {R} )}
[
α
,
b
]
⊆
(
−
∞
,
b
]
{\displaystyle [\alpha ,b]\subseteq (-\infty ,b]}
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
−
∞
b
f
(
x
)
d
x
=
lim
α
→
−
∞
∫
α
b
f
(
x
)
d
x
{\displaystyle \int _{-\infty }^{b}f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\int _{\alpha }^{b}f(x)\mathrm {d} x}
또한, 실수 함수
f
:
R
→
R
{\displaystyle f\colon \mathbb {R} \to \mathbb {R} }
[
α
,
β
]
⊆
R
{\displaystyle [\alpha ,\beta ]\subseteq \mathbb {R} }
f
{\displaystyle f}
이상 적분 은 다음과 같은 극한이다.
∫
−
∞
∞
f
(
x
)
d
x
=
lim
α
→
−
∞
lim
β
→
∞
∫
α
β
f
(
x
)
d
x
=
lim
α
→
−
∞
∫
α
0
f
(
x
)
d
x
+
lim
β
→
∞
∫
0
β
f
(
x
)
d
x
{\displaystyle \int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\lim _{\beta \to \infty }\int _{\alpha }^{\beta }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\int _{\alpha }^{0}f(x)\mathrm {d} x+\lim _{\beta \to \infty }\int _{0}^{\beta }f(x)\mathrm {d} x}
이와 같이 적분 상한이 양의 무한대이거나, 적분 하한이 음의 무한대인 이상 적분을 무한대 적분 (無限大積分)이라고 한다.
(수렴하지 않을 수 있는) 이상 적분에 대하여 코시 주요값 (Cauchy主要-, 영어 : Cauchy principal value ) 또는 코시 주치 (Cauchy主値)라 불리는 값을 줄 수 있다. 즉, 이상 적분
∫
a
b
f
(
x
)
d
x
=
lim
γ
1
→
c
0
+
0
lim
δ
1
→
c
1
−
0
⋯
lim
γ
n
→
c
n
−
1
+
0
lim
δ
n
→
c
n
−
0
∑
k
=
1
n
∫
γ
k
δ
k
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\gamma _{1}\to c_{0}+0}\lim _{\delta _{1}\to c_{1}-0}\cdots \lim _{\gamma _{n}\to c_{n-1}+0}\lim _{\delta _{n}\to c_{n}-0}\sum _{k=1}^{n}\int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x}
의 코시 주요값 은
PV
∫
a
b
f
(
x
)
d
x
=
lim
ϵ
→
0
+
0
∑
k
=
1
n
∫
c
k
−
1
+
ϵ
c
k
−
ϵ
f
(
x
)
d
x
{\displaystyle \operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\sum _{k=1}^{n}\int _{c_{k-1}+\epsilon }^{c_{k}-\epsilon }f(x)\mathrm {d} x}
이다. 특수한 경우의 이상 적분의 코시 주요 값은 다음과 같다.
이상 적분
코시 주요값
∫
a
b
f
(
x
)
d
x
=
lim
α
→
a
+
0
lim
β
→
b
−
0
∫
α
β
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\lim _{\beta \to b-0}\int _{\alpha }^{\beta }f(x)\mathrm {d} x}
PV
∫
a
b
f
(
x
)
d
x
=
lim
ϵ
→
0
+
0
∫
a
+
ϵ
b
−
ϵ
f
(
x
)
d
x
{\displaystyle \operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\int _{a+\epsilon }^{b-\epsilon }f(x)\mathrm {d} x}
∫
a
b
f
(
x
)
d
x
=
lim
δ
→
c
−
0
lim
γ
→
c
+
0
(
∫
a
δ
f
(
x
)
d
x
+
∫
γ
b
f
(
x
)
d
x
)
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\delta \to c-0}\lim _{\gamma \to c+0}\left(\int _{a}^{\delta }f(x)\mathrm {d} x+\int _{\gamma }^{b}f(x)\mathrm {d} x\right)}
PV
∫
a
b
f
(
x
)
d
x
=
lim
ϵ
→
0
+
0
(
∫
a
c
−
ϵ
f
(
x
)
d
x
+
∫
c
+
ϵ
b
f
(
x
)
d
x
)
{\displaystyle \operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\left(\int _{a}^{c-\epsilon }f(x)\mathrm {d} x+\int _{c+\epsilon }^{b}f(x)\mathrm {d} x\right)}
∫
−
∞
∞
f
(
x
)
d
x
=
lim
α
→
−
∞
lim
β
→
∞
∫
α
β
f
(
x
)
d
x
{\displaystyle \int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\lim _{\beta \to \infty }\int _{\alpha }^{\beta }f(x)\mathrm {d} x}
PV
∫
−
∞
∞
f
(
x
)
d
x
=
lim
γ
→
∞
∫
−
γ
γ
f
(
x
)
d
x
{\displaystyle \operatorname {PV} \int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\gamma \to \infty }\int _{-\gamma }^{\gamma }f(x)\mathrm {d} x}
적분 가능 함수의 이상 적분은 수렴하며, 그 값은 이상 적분을 사용하지 않은 적분 값과 같다.
이상 적분은 급수 와 달리 수렴(또는 절대 수렴)하더라도, 함수가 0에 수렴할 필요가 없으며, 유계 함수일 필요가 없다.
극한값이 존재하면 이상적분은 수렴한다. 또한 이상적분이 무한대로 발산하는 경우 또한 존재한다.
lim
b
→
∞
∫
1
b
1
x
d
x
=
∞
.
{\displaystyle \lim _{b\to \infty }\int _{1}^{b}{\frac {1}{x}}\,dx=\infty .}
어떤 이상적분은 특별한 방향없이 발산하는 경우도 있다.
lim
b
→
∞
∫
1
b
x
sin
x
d
x
,
{\displaystyle \lim _{b\to \infty }\int _{1}^{b}x\sin x\,dx,}
위와 같은 적분은 확장된 실수 내에서도 값이 존재하지 않는다.
적분 구간의 양 끝값이 무한인 경우, 임의의 실수 c에 대해
∫
−
∞
c
f
(
x
)
d
x
{\displaystyle \int _{-\infty }^{c}f(x)\,dx}
∫
c
∞
f
(
x
)
d
x
{\displaystyle \int _{c}^{\infty }f(x)\,dx}
∫
−
∞
∞
f
(
x
)
d
x
=
∫
−
∞
c
f
(
x
)
d
x
+
∫
c
∞
f
(
x
)
d
x
{\displaystyle \int _{-\infty }^{\infty }f(x)\,dx=\int _{-\infty }^{c}f(x)\,dx+\int _{c}^{\infty }f(x)\,dx}
만약 둘 중 하나라도 발산한다면 적분 구간의 양 끝값이 무한인 f(x)의 이상적분은 발산한다.
함수에 따라서는 이러한 적분구간의 양 끝값이 무한인 경우라도 적분값이 수렴하는 경우도 있다. 예를 들어 가우스 적분 (Gaussian integral)
∫
−
∞
∞
e
−
x
2
d
x
=
π
{\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}}
이상 적분과 관련된 가장 주요문제는 다음 두 가지이다.
극한이 존재하는가?
극한을 계산할 수 있는가? 첫 번째 질문은 해석학 의 문제이다. 두 번째 질문은 미적분학 에서 다루지만 종종 복소해석학 의 경로적분법 (contour integration)이나 푸리에 해석 등의 고급 기법을 동원하는 경우도 있다.
![{\displaystyle f\colon [a,b]\setminus \{-\infty ,\infty \}\to \mathbb {R} \qquad (-\infty \leq a<b\leq \infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5c3b2aeeaacfacf5888f7ebca01786e634652f4)
![{\displaystyle [\gamma _{k},\delta _{k}]\subseteq (c_{k-1},c_{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e12739259f2d7d846075afcc5681083ce104c2f)
![{\displaystyle [a,\beta ]\subseteq [a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f3c2d030f7582fef25b5437b556d22f11ab2ed3)
![{\displaystyle f\colon (a,b]\to \mathbb {R} \qquad (-\infty \leq a<b<\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/114d1bb227786a0fcb9852f985c7e27e66ea6aa8)
![{\displaystyle [\alpha ,b]\subseteq (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97f2259625b2f243236dfa4a3b725414a54e3ddf)
![{\displaystyle [\alpha ,\beta ]\subseteq (a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88f8b32136827f4c9834cde32f0482e28b4f5df)
![{\displaystyle f\colon [a,b]\to \mathbb {R} \qquad (-\infty <a<c<b<\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f12b3c412ec9b103add50a50cd83dc3c6c0cdf17)
![{\displaystyle [a,\delta ]\subseteq [a,c)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc035ec255900319771dcbe9de7bd9cb7591ac07)
![{\displaystyle [\gamma ,b]\subseteq (c,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d49febfe78b40c890258deb4f839b1c16fb84d5e)
![{\displaystyle [a,\beta ]\subseteq [a,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76960b5d66df7bb75bed35ca75bab476e75ad2ec)
![{\displaystyle f\colon (-\infty ,b]\to \mathbb {R} \qquad (b\in \mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5837e9741ac9b3afcf9d95d9de02505aab26354b)
![{\displaystyle [\alpha ,b]\subseteq (-\infty ,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53fc4510f9e9a31e518e6344ba66967b3303b743)
![{\displaystyle [\alpha ,\beta ]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcacf465867c7c5a1a5c6b749ad406416df163b1)
이 부분의 본문은 코시 주요값입니다.
![{\displaystyle \lim _{b\to \infty }\int \limits _{1}^{b}{\frac {1}{x^{2}}}\,dx=\lim _{b\to \infty }\left[-{\frac {1}{b}}+{\frac {1}{1}}\right]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc0b437d73cfe54a8f7076fd609c874bc966b61)
![{\displaystyle \lim _{a\to 0^{+}}\int \limits _{a}^{1}{\frac {1}{\sqrt {x}}}\,dx=\lim _{a\to 0^{+}}\left[2{\sqrt {1}}-2{\sqrt {a}}\right]=2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fb9ba8d75cc5a0fa76f62aede153bb9b495229a)