전곡률

곡선의 미분 기하학에서 몰입된 평면 곡선의 전곡률은 호 길이 매개화 곡선을 따른 곡률의 적분이다.

\int _{a}^{b}k(s)\,ds=2\pi N.

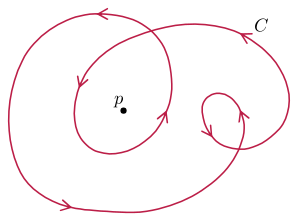
닫힌 곡선의 전곡률은 항상 2π의 정수 N배이다. 여기서 N은 곡선의 지표 또는 회전수라고 한다. 이는 원점에 대한 단위 접벡터의 감김 수 또는 동등하게 곡선의 각 점에 할당된 단위원에 해당 점의 단위 속도 벡터를 지정하는 사상의 브라우어 차수이다. 이 사상은 곡면에 대한 가우스 사상과 비슷하다.

곡면과의 비교

국소적인 기하 불변량인 곡률과 전역적인 위상 불변량인 지표 사이의 이러한 관계는 가우스-보네 정리 와 같은 고차원 리만 기하학 결과의 특징이다.

불변성

휘트니-그라우슈타인 정리에 따르면 전곡률은 곡선의 정규 호모토피 하에서 불변이다. 이는 가우스 사상의 차수이다. 그러나 호모토피 하에서는 불변이 아닙니다. 꼬임(뾰족한 끝)을 통과하면 회전 수가 1씩 변경된다.

이에 반해, 점 주위의 감김 수는 그 점을 통과하지 않는 호모토피에서는 불변이고, 점을 통과하면 1씩 변한다.

일반화

전곡률 2π인 닫힌 다각형 체인 .

유한한 일반화는 삼각형 또는 보다 일반적으로 단순 다각형의 외부 각도를 더하면 360°=2π가 된다는 것이다. 이는 회전수 1에 해당한다.

곡선의 절대 전곡률은 전곡률과 거의 같은 방식으로 정의되지만 부호 있는 곡률 대신 곡률의 절대값을 사용한다. 평면의 볼록한 곡선의 경우 2π이고 볼록하지 않은 곡선의 경우 더 크다.^[1] 또한 $γ$ 에 전개 가능한 접선을 평면으로 편평화하고 결과 곡선의 전곡률을 계산하여 더 높은 차원 공간의 곡선으로 일반화할 수 있다. 즉, $n$ 차원 공간에서 곡선의 전곡률은 다음과 같다.

\int _{a}^{b}\left|\gamma ''(s)\right|\operatorname {sgn} \kappa _{n-1}(s)\,ds

여기서 $κ n -1$ 은 마지막 프레네 곡률(곡선의 비틀림)이고 $sgn$ 은 부호 함수이다.

주어진 매듭을 나타내는 3차원 곡선의 최소 절대 전곡률은 매듭 불변량이다. 이 불변량은 매듭지어지지 않은 매듭의 경우 2π이지만 페리-밀너 정리에 따르면 매듭의 경우 최소 4π이다.^[2]

각주

↑ Chen, Bang-Yen (2000), 〈Riemannian submanifolds〉, 《Handbook of differential geometry, Vol. I》, North-Holland, Amsterdam, 187–418쪽, doi:10.1016/S1874-5741(00)80006-0, MR 1736854
↑ Milnor, John W. (1950), “On the Total Curvature of Knots”, 《Annals of Mathematics》, Second Series 52 (2): 248–257, doi:10.2307/1969467, JSTOR 1969467

추가 읽기

Kuhnel, Wolfgang (2005), 《Differential Geometry: Curves - Surfaces - Manifolds》 2판, American Mathematical Society, ISBN 978-0-8218-3988-1 (translated by Bruce Hunt)
Sullivan, John M. (2008), 〈Curves of finite total curvature〉, 《Discrete differential geometry》, Oberwolfach Semin. 38, Birkhäuser, Basel, 137–161쪽, arXiv:math/0606007, doi:10.1007/978-3-7643-8621-4_7, MR 2405664, S2CID 117955587

[1] Chen, Bang-Yen (2000), 〈Riemannian submanifolds〉, 《Handbook of differential geometry, Vol. I》, North-Holland, Amsterdam, 187–418쪽, doi:10.1016/S1874-5741(00)80006-0, MR 1736854

[2] Milnor, John W. (1950), “On the Total Curvature of Knots”, 《Annals of Mathematics》, Second Series 52 (2): 248–257, doi:10.2307/1969467, JSTOR 1969467

[1]

[2]