정규 분포

확률론과 통계학에서 정규 분포(正規 分布, 영어: normal distribution) 또는 가우스 분포(Gauß 分布, 영어: Gaussian distribution)는 연속 확률 분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는 데에 자주 사용되며, 이것은 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다.

정규 분포

확률 밀도 함수
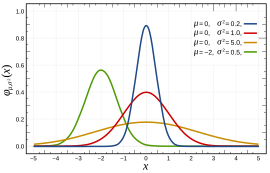붉은 색은 표준정규분포
누적 분포 함수
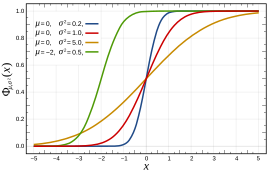확률밀도함수의 색과 같은 색
매개변수	$\mu$ 평균 $\sigma ^{2}>0$ 분산
지지집합	$x\in (-\infty ;+\infty )\!$
확률 밀도	${\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)\!$
누적 분포	${\frac {1}{2}}\left(1+\mathrm {erf} \,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!$
기댓값	$\mu$
중앙값	$\mu$
최빈값	$\mu$
분산	$\sigma ^{2}$
비대칭도	0
첨도	0
엔트로피	$\ln \left(\sigma {\sqrt {2\,\pi \,e}}\right)\!$
적률생성함수	$M_{X}(t)=\exp \left(\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}\right)$
특성함수	$\phi _{X}(t)=\exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)$

정규분포는 2개의 매개 변수 평균 $\mu$와 표준편차 $\sigma$에 대해 모양이 결정되고, 이때의 분포를 $\mathrm {N} (\mu ,\sigma ^{2})$로 표기한다. 특히, 평균이 0이고 표준편차가 1인 정규분포 $\mathrm {N} (0,1)$을 표준 정규 분포(standard normal distribution)라고 한다.

역사

정규분포는 아브라암 드무아브르가 1733년 쓴 글에서 특정 이항 분포의 $n$이 클 때 그 분포의 근사치를 계산하는 것과 관련하여 처음 소개되었고 이 글은 그의 저서 《우연의 교의》(The Doctrine of Chances) 2판(1738년)에 다시 실렸다. 피에르시몽 라플라스는 그의 저서 《확률론의 해석이론》(Théorie analytique des probabilités)(1812년)에서 이 결과를 확장하였고 이는 오늘날 드무아브르-라플라스의 정리로 알려져있다.

라플라스는 실험 오차를 분석하면서 정규분포를 사용했다. 1805년에는 아드리앵마리 르장드르가 매우 중요한 방법인 최소제곱법을 도입했다. 카를 프리드리히 가우스는 이 방법을 1794년부터 사용해왔다고 주장했는데 1809년에는 실험 오차가 정규분포를 따른다는 가정하에 최소제곱법을 이론적으로 엄밀히 정당화했다.

성질

• 정규분포에서는 기댓값, 최빈값, 중앙값이 모두 $\mu$이다. 정규분포의 기댓값은 다음과 같이 계산할 수 있다.

${\begin{aligned}{\bar {x}}&=\int _{-\infty }^{\infty }{\frac {x}{\sigma {\sqrt {2\pi }}}}\;\exp \left[-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right]\\&={\frac {{\sqrt {2}}\sigma }{\sqrt {\pi }}}\int _{-\infty }^{\infty }y\exp[-y^{2}]dy+{\frac {\mu }{\sqrt {\pi }}}\int _{-\infty }^{\infty }\exp[-y^{2}]dy\end{aligned}}$

위에서 첫 번째 적분은 홀함수의 적분으로 0이고 두 번째 적분은 가우스 적분으로 적분값이 ${\sqrt {\pi }}$로 잘 알려져 있다. 따라서 기댓값은 $\mu$다.

• 정규분포는 절대근사한다.
• 정규분포는 평균과 표준편차가 주어져 있을 때 엔트로피를 최대화하는 분포이다.
• 정규분포곡선은 좌우 대칭이며 하나의 꼭지를 가진다.
• 정규분포는 중앙치에 사례 수가 모여있고, 양극단으로 갈수록 X축에 무한히 접근하지만 X축에 닿지는 않는다.

표준 정규 분포

정규 분포 밀도 함수에서 $Z={\frac {X-\mu }{\sigma }}$를 통해 X(원점수)를 Z(Z점수)로 정규화함으로써 평균이 0, 표준편차가 1인 표준정규분포를 얻을 수 있다.

z-분포라고도 부른다. z-분포로 하는 검정(test)을 z검정(z-test)이라고 한다.

불확실성

$P[\mu -k\sigma <X<\mu +k\sigma ]$에서 k값이 변화함에 따라 구해지는 $\pm k\sigma$값을 불확실성(uncertainty)이라고 한다. 예를 들어 $\pm 1.645\sigma$를 90% 불확실성, $\pm 1.960\sigma$는 95% 불확실성, $\pm 2.576\sigma$은 99% 불확실성이다. 특히, $\pm 0.674\sigma$를 50% 불확실성이라고 하며, 확률오차(probable error)라고도 한다. 이는 관측값이 전체 관측값의 50%에 있을 확률을 의미한다.

같이 보기

• 가우스 함수
• 표본 크기
• F 분포
• 표준정규분포표

참고 문헌

• 이재기; 최석근; 박경식; 정성혁 (2013). 《측량학1》 2판. 형설출판사. ISBN 978-89-472-7336-7. 
• (구글북스, Pierre Simon marquis de Laplace, Théorie analytique des probabilités 1812)https://books.google.co.kr/books?id=nQwAAAAAMAAJ&printsec=frontcover&hl=ko&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
• (구글북스,The Doctrine of Chances , 1st edition ,Abraham de Moivre 1718)https://books.google.com/books?id=3EPac6QpbuMC

외부 링크

• 위키미디어 공용에 정규 분포 관련 미디어 분류가 있습니다.
• “Normal distribution”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Normal distribution”. 《Wolfram MathWorld》 (영어). Wolfram Research.