위키백과

정다각형 테셀레이션

(정규 타일링에서 넘어옴)

정다각형 타일링의 예시

정규 타일링은 한 종류의 정다각형이 쓰인다.
준정규 타일링 또는 균일 타일링은 꼭짓점 배치가 한 가지이지만, 두 종류 이상의 정다각형이 쓰인다.

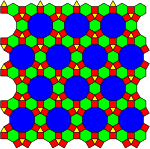k-균일 타일링은 k가지 꼭짓점 배치가 있고, 두 종류 이상의 정다각형이 쓰인다.
모서리 대 모서리로 만나지 않는 타일링은 다른 크기의 정다각형이 있을 수 있다.

정다각형 타일링은 정다각형으로 유클리드 평면을 채우는 타일링으로, 고대부터 널리 쓰여 왔다. 1619년 케플러의 책 《세계의 조화》에서 이 테셀레이션에 대해 최초로 체계적이며 수학적으로 접근했다.

유클리드 타일링의 표기법

편집

유클리드 타일링은 대부분 Cundy & Rollett의 표기법을 사용한다.[1] 이 표기법은 (1) 꼭짓점의 개수, (2) 각 꼭짓점이 접하는 다각형의 개수(시계 방향), (3) 그 다각형 각각의 변의 개수를 나타낸다. 예를 들어서 36; 36; 34.6에서 2가지 다른 꼭짓점 배치를 가지는 3개의 꼭짓점이 있다는 것을 알 수 있다. 따라서 이 타일링을 '3-균일(2-꼭짓점 종류)' 타일링이라고 한다. 쪼개서 보면, 36; 36 (추이가 다름) 또는 (36)2에서 정삼각형 6개가 모인 꼭짓점이 2개라는 것을 알 수 있다. 마지막 꼭짓점 34.6에서는 4개의 인접한 변 길이가 같은 정삼각형과 하나의 정육각형이 모여 있다는 걸 알 수 있다.

하지만 이 표기법은 형태와 특이성이 애매해서 두 가지 큰 문제가 있다.[2] 첫 번째, k-균일 타일링에서 이 표기법은 꼭짓점들 사이에 관계를 설명하지 않는다. 따라서 표기법만 가지고 평면을 채우는 건 불가능하다. 두 번째, 일부 테셀레이션은 표기법이 같다. 육각형의 상대적인 위치가 다르다는 것으로만 다른 테셀레이션이라는 걸 알 수 있는 것도 있다. 즉 이 표기법이 각 테셀레이션을 구별할 수 없다는 것이다.(각 테셀레이션에 대해 특이하지 않다)

이런 문제를 해결하기 위한 GomJau-Hogg의 표기법[3]은 테셀레이션과 이중 격자(double-layer grids)의 세대(generation)와 표기법에 대해, 위의 연구와 표기법을 살짝 변형해 2012년 발표되었다.[2] 무료 온라인 앱 Antwerp v3.0은 GomJau-Hogg의 표기법으로 직접 알 수 있는 도형 배치 단계, 반복되는 회전과 반사 변환을 통해서 무수히 많은 세대의 정다각형 타일링을 표현할 수 있다.[4]

정규 타일링

편집

Grünbaum과 Shephard(section 1.3)에 따르면, 정규 타일링은 타일링의 대칭군이 기점(영어판)에 추이적으로 작용하는 것을 말한다. 여기서 기(旗, flag)는 한 꼭짓점, 그 꼭짓점에 인접한 한 모서리, 그 꼭짓점과 모서리에 동시에 인접한 한 면 (기하학) 3가지를 말한다. 다시 말해서 어떤 쌍의 기점에도, 첫 번째에서 두 번째 기점으로의 대칭 작용이 있다는 것이다.

정규 타일링은 합동인 정다각형을 통해 모서리 대 모서리로 만들어지는 타일링과 동치이다. 세 가지 정규 타일링은 정삼각형 6개, 정사각형 4개, 정육각형 3개가 한 꼭짓점에 모일 때 가능하다.

정규 타일링이 3개뿐이라는 것은 비교적 쉽게 증명할 수 있다. 정n각형의 한 내각의 크기는  인데, 정규 타일링은 모서리 대 모서리 타일링이고 한 종류의 정다각형만 사용하므로 한 내각의 크기가 360°의 약수여야 한다. n이 최소인 3일 때 60°이고 n값에 상관없이 180°보다 작으므로 가능한 경우는 360°/6=60°, 360°/5=72°, 360°/4=90°, 360°/3=120°가 있다. 이 중 실제로 가능한 것은 60°의 정삼각형, 90°의 정사각형, 120°의 정육각형 뿐이다.[5]

정규 타일링 (3)
p6m, *632 p4m, *442
     
 
C&R: 36
GJ-H: 3/m30/r(h2)
(t = 1, e = 1) 		 
C&R: 63
GJ-H: 6/m30/r(h1)
(t = 1, e = 1) 		 
C&R: 44
GJ-H: 4/m45/r(h1)
(t = 1, e = 1)

C&R: Cundy & Rollet의 표기법
GJ-H: GomJau-Hogg의 표기법

준정규 타일링

편집

점추이는 임의의 한 쌍의 꼭짓점에 첫 번째에서 두 번째 꼭짓점으로 가는 대칭 작용이 있다는 것이다.[6]

기(flag)추이의 조건이 점추이 중 하나로 약해지면, 모서리 대 모서리라는 조건이 있을 때 8개의 타일링이 더 가능하다. 이를 아르키메데스, 균일(고른), 준정규 타일링이라고 한다. 34.6 (다듬은 정육각형) 타일링은 카이랄성을 지녀서 두 거울상이 있다. 다른 나머지 정규 또는 준정규 타일링은 카이랄성이 없다.

고른 타일링 (8)
p6m, *632
 

 
C&R: 3.122
GJ-H: 12-3/m30/r(h3)
(t = 2, e = 2)
t{6,3} 		 

 
C&R: 3.4.6.4
GJ-H: 6-4-3/m30/r(c2)
(t = 3, e = 2)
rr{3,6} 		 

 
C&R: 4.6.12
GJ-H: 12-6,4/m30/r(c2)
(t = 3, e = 3)
tr{3,6} 		 

 
C&R: (3.6)2
GJ-H: 6-3-6/m30/r(v4)
(t = 2, e = 1)
r{6,3}
 

 
C&R: 4.82
GJ-H: 8-4/m90/r(h4)
(t = 2, e = 2)
t{4,4} 		 

 
C&R: 32.4.3.4
GJ-H: 4-3-3,4/r90/r(h2)
(t = 2, e = 2)
s{4,4} 		 

 
C&R: 33.42
GJ-H: 4-3/m90/r(h2)
(t = 2, e = 3)
{3,6}:e 		 

 
C&R: 34.6
GJ-H: 6-3-3/r60/r(h5)
(t = 3, e = 3)
sr{3,6}

C&R: Cundy & Rollet의 표기법
GJ-H: GomJau-Hogg의 표기법

Grünbaum과 Shephard는 이런 타일링이 각 꼭짓점의 타일 배치가 같다는 부분적(local) 특성만 지키기 때문에 아르키메데스라고 불렀다. 또 점특이의 전체적(global) 특성을 만족하기 때문에 균일하다(고르다)고 했다. 평면에서는 같은 집합의 타일링을 말하지만, 다른 공간에서는 아르키메데스 타일링 중 고르지 않은 것도 있다.

같이 보기

편집

각주

편집
  1. ↑ Cundy, H.M.; Rollett, A.P. (1981). 《Mathematical Models;》. Stradbroke (UK): Tarquin Publications. 
  2. ↑ 가 나 Gomez-Jauregui, Valentin al.; Otero, Cesar; 외. (2012). “Generation and Nomenclature of Tessellations and Double-Layer Grids”. 《Journal of Structural Engineering》 138 (7). doi:10.1061/(ASCE)ST.1943-541X.0000532. 
  3. ↑ Gomez-Jauregui, Valentin; Hogg, Harrison; 외. (2021). “GomJau-Hogg’s Notation for Automatic Generation of k-Uniform Tessellations with ANTWERP v3.0”. 《Symmetry》 13 (12). doi:10.3390/sym13122376. 
  4. ↑ Hogg, Harrison; Gomez-Jauregui, Valentin. < “Antwerp 3.0”. 
  5. ↑ “다각형의 변신 (2부) 꽃담에 숨은 다각형의 원리”. 《EBS MATH > 중1 > 기하》. 
  6. ↑ Critchlow, K. (1969). 《Order in Space: A Design Source Book,》. London: Thames and Hudson. 60–61쪽. 
원본 주소 "https://ko.wiki.x.io/w/index.php?title=정다각형_테셀레이션&oldid=37905613#정규_타일링"