지수 분포
지수분포(指數分布, 영어: exponential distribution)는 연속 확률 분포의 일종이다. 사건이 서로 독립적일 때, 일정 시간 동안 발생하는 사건의 횟수가 푸아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기 시간은 지수분포를 따른다.[1] 이는 기하분포와 유사한 측면이 있다.
| 확률 밀도 함수 | |
|---|---|
| |
| 누적 분포 함수 | |

| |
| 기호 | |
| 매개변수 | : 빈도 |
| 지지집합 | |
| 확률 밀도 | |
| 누적 분포 | |
| 기댓값 | |
| 중앙값 | |
| 최빈값 | |
| 분산 | |
| 비대칭도 | |
| 첨도 | |
| 엔트로피 | |
| 적률생성함수 | |
| 특성함수 | |
특징
편집확률 밀도 함수
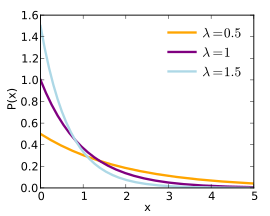
편집지수분포의 확률 밀도 함수는
로 정의된다. 단위 계단 함수를 이용해 정의하면,
가 된다. 여기서 λ은 빈도를 나타내는 모수이며, 확률변수 X는 [0, ∞)에서 정의된다.
누적 분포 함수
편집지수분포의 누적 분포 함수는
혹은
이다.
성질
편집기댓값과 분산
편집확률변수 X가 빈도 λ를 모수로 갖는 지수분포를 따른다면, 기댓값은
으로 단위 시간당 사건이 λ회 발생한다면, 사건 사이에 평균적으로 1/λ시간만큼 기다릴 것이라는 것을 의미한다. 분산은
이다.
각주
편집- ↑ Doane, David P.; Lori E. Seward, 최필선, 민인식 공역. 《경영경제 통계학》. McGraw-Hill. 275쪽. ISBN 978-89-6055-098-8.
같이 보기
편집| 이 글은 수학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. | |
| 이 글은 통계학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |













