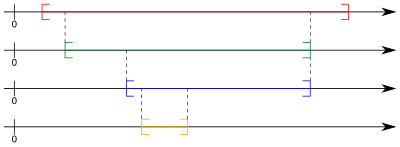
수학 에서 축소구간열 (縮小區間列, sequence of nested intervals )은 각 구간이 바로 앞 구간의 부분 집합 인 구간들의 열 이다. 축소구간정리 (縮小區間定理, 영어 : nested intervals theorem )에 따르면, 닫힌구간 으로 구성된 축소구간열은 적어도 하나의 공통 원소를 갖는다.
축소하는 닫힌구간 들의 열
축소구간열 은 임의의 자연수
n
∈
N
{\displaystyle n\in \mathbb {N} }
I
n
⊇
I
n
+
1
{\displaystyle I_{n}\supseteq I_{n+1}}
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
축소구간열
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
I
n
{\displaystyle I_{n}}
a
n
,
b
n
∈
R
{\displaystyle a_{n},b_{n}\in \mathbb {R} }
n
∈
N
{\displaystyle n\in \mathbb {N} }
|
I
n
|
≥
|
I
n
+
1
|
{\displaystyle |I_{n}|\geq |I_{n+1}|}
|
I
n
|
=
b
n
−
a
n
{\displaystyle |I_{n}|=b_{n}-a_{n}}
구간의 길이 이다.)
a
n
≤
a
n
+
1
≤
b
n
+
1
≤
b
n
{\displaystyle a_{n}\leq a_{n+1}\leq b_{n+1}\leq b_{n}}
{
a
n
∉
I
n
a
n
+
1
∈
I
n
+
1
⟹
a
n
<
a
n
+
1
{\displaystyle {\begin{cases}a_{n}\notin I_{n}\\a_{n+1}\in I_{n+1}\end{cases}}\implies a_{n}<a_{n+1}}
{
b
n
∉
I
n
b
n
+
1
∈
I
n
+
1
⟹
b
n
+
1
<
b
n
{\displaystyle {\begin{cases}b_{n}\notin I_{n}\\b_{n+1}\in I_{n+1}\end{cases}}\implies b_{n+1}<b_{n}}
구간열
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
모두 닫힌구간 이다. 즉, 임의의 자연수
n
∈
N
{\displaystyle n\in \mathbb {N} }
I
n
=
cl
I
n
{\displaystyle I_{n}=\operatorname {cl} I_{n}}
축소구간열이다. 즉, 임의의 자연수
n
∈
N
{\displaystyle n\in \mathbb {N} }
I
n
⊇
I
n
+
1
{\displaystyle I_{n}\supseteq I_{n+1}}
축소구간정리 에 따르면, 이 구간열의 교집합 은 공집합 이 아닌 (퇴화 또는 비퇴화) 닫힌구간이다. 즉,
⋂
n
∈
N
I
n
=
[
a
,
b
]
{\displaystyle \bigcap _{n\in \mathbb {N} }I_{n}=[a,b]}
이게 되는 두 실수
a
≤
b
{\displaystyle a\leq b}
특히,
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
lim
n
→
∞
|
I
n
|
=
0
{\displaystyle \lim _{n\to \infty }|I_{n}|=0}
수렴 한다.그렇다면,
a
=
b
{\displaystyle a=b}
한원소 집합 이다.
⋂
n
∈
N
I
n
=
{
a
=
b
}
{\displaystyle \bigcap _{n\in \mathbb {N} }I_{n}=\{a=b\}}
축소구간정리는 코시 성질 과 동치이다. 즉, 아르키메데스 성질 을 덧붙이면 실수의 완비성 을 나타내는 여러 공리들과 동치가 된다. 문헌에 따라서는 세 번째 조건이 빠진 서술을 뜻하기도 하는데, 이 또한 더 강한 조건의 축소구간정리와 동치이다.
다음 구간열들은 축소구간정리의 전제 조건을 만족하며, 따라서 교집합이 (퇴화 또는 비퇴화) 닫힌구간이다.
⋂
n
∈
N
[
1
−
1
n
,
2
+
1
n
]
=
[
1
,
2
]
{\displaystyle \bigcap _{n\in \mathbb {N} }\left[1-{\frac {1}{n}},2+{\frac {1}{n}}\right]=[1,2]}
⋂
n
∈
N
[
1
−
1
n
,
1
+
1
n
]
=
{
1
}
{\displaystyle \bigcap _{n\in \mathbb {N} }\left[1-{\frac {1}{n}},1+{\frac {1}{n}}\right]=\{1\}}
일반적인 축소구간열의 교집합은 공집합이 아닌 (퇴화 또는 비퇴화) 닫힌구간일 필요가 없다. 즉, 열린구간 이나 공집합 등일 수 있다.
⋂
n
∈
N
(
0
,
1
n
)
=
⋂
n
∈
N
(
0
,
1
n
]
=
∅
{\displaystyle \bigcap _{n\in \mathbb {N} }\left(0,{\frac {1}{n}}\right)=\bigcap _{n\in \mathbb {N} }\left(0,{\frac {1}{n}}\right]=\varnothing }
⋂
n
∈
N
(
0
,
1
)
=
(
0
,
1
)
{\displaystyle \bigcap _{n\in \mathbb {N} }(0,1)=(0,1)}
축소구간열의 "닫힌구간" 전제 조건은 다음과 같은 조건으로 바꿀 수 있다.
축소구간열
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
임의의 자연수
n
∈
N
{\displaystyle n\in \mathbb {N} }
a
n
<
a
n
+
1
<
b
n
+
1
<
b
n
{\displaystyle a_{n}<a_{n+1}<b_{n+1}<b_{n}}
를 만족시킨다면, 교집합은 역시 공집합이 아닌 (퇴화 또는 비퇴화) 닫힌구간이다. 이는
⋂
n
∈
N
I
n
=
⋂
n
∈
N
cl
I
n
{\displaystyle \bigcap _{n\in \mathbb {N} }I_{n}=\bigcap _{n\in \mathbb {N} }\operatorname {cl} I_{n}}
이기 때문이다. 여기서
cl
I
n
{\displaystyle \operatorname {cl} I_{n}}
폐포 이며, 이들은 닫힌구간으로 구성된 축소 구간열을 이룬다. 예를 들어, 다음과 같다.
⋂
n
∈
N
(
−
1
n
,
1
n
)
=
⋂
n
∈
N
[
−
1
n
,
1
n
]
=
{
0
}
{\displaystyle \bigcap _{n\in \mathbb {N} }\left(-{\frac {1}{n}},{\frac {1}{n}}\right)=\bigcap _{n\in \mathbb {N} }\left[-{\frac {1}{n}},{\frac {1}{n}}\right]=\{0\}}
⋂
n
∈
N
[
0
,
1
n
)
=
⋂
n
∈
N
[
0
,
1
n
]
=
{
0
}
{\displaystyle \bigcap _{n\in \mathbb {N} }\left[0,{\frac {1}{n}}\right)=\bigcap _{n\in \mathbb {N} }\left[0,{\frac {1}{n}}\right]=\{0\}}
비슷하게, 축소구간열
(
I
n
)
n
∈
N
{\displaystyle (I_{n})_{n\in \mathbb {N} }}
임의의 자연수
n
∈
N
{\displaystyle n\in \mathbb {N} }
a
n
<
sup
n
∈
N
a
n
≤
sup
n
∈
N
b
n
<
b
n
{\displaystyle a_{n}<\sup _{n\in \mathbb {N} }a_{n}\leq \sup _{n\in \mathbb {N} }b_{n}<b_{n}}
를 만족시킨다면, 교집합은 역시 공집합이 아닌 (퇴화 또는 비퇴화) 닫힌구간이다.
축소구간정리는 유클리드 공간 을 비롯한 거리 공간 으로 일반화할 수 있다.
거리 공간
X
{\displaystyle X}
부분 집합 의 열
(
K
n
)
n
∈
N
{\displaystyle (K_{n})_{n\in \mathbb {N} }}
임의의
n
∈
N
{\displaystyle n\in \mathbb {N} }
K
n
{\displaystyle K_{n}}
콤팩트 집합 이다.
임의의
n
∈
N
{\displaystyle n\in \mathbb {N} }
K
n
⊇
K
n
+
1
{\displaystyle K_{n}\supseteq K_{n+1}}
그렇다면, 그들의 교집합은 공집합이 아니다. 또한, 추가적으로 다음 조건을 만족시킨다고 하자.
lim
n
→
∞
diam
K
n
=
0
{\displaystyle \lim _{n\to \infty }\operatorname {diam} K_{n}=0}
거리 공간의 지름 이 0으로 수렴한다.그렇다면, 그들의 교집합은 한원소 집합 이다.
위상 공간 속, 공집합이 아닌 콤팩트 닫힌집합 의 하강 열의 교집합은 공집합이 아니다.