콘웨이 다면체 표기법
이 문서의 내용은 출처가 분명하지 않습니다. (2021년 2월) |
콘웨이 다면체 표기법은 존 호턴 콘웨이가 개발한 다면체의 표기법이다.
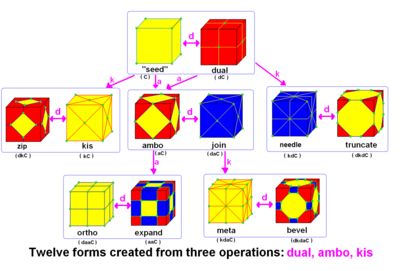
기하학에서, 존 호튼 콘웨이가 발명하고 조지 W. 하트가 장려한 콘웨이 다면체 표기법은 다양한 접두사 연산에 의해 수정된 씨앗 다면체에 기초한 다면체를 묘사하기 위해 사용된다.
콘웨이와 하트는 케플러가 정의한 절단 연산자를 사용하여 동일한 대칭의 관련 다면체를 만드는 아이디어를 확장했다. 예를 들어 tC는 잘린 큐브를 나타내고 taC는 다음과 같이 구문 분석한다.
스타일 T(aC)를 표시한다.}, 는 (위상적으로) 깎은 정육면체이다. 가장 간단한 연산자 이중 꼭지점과 면 요소를 바꾼다. 예를 들어, 이중 큐브는 8면체이다. dC=O. 이러한 연산자는 직렬로 적용되어 많은 고차 다면체가 생성될 수 있다. Hart가 r과 p를 더하는 동안 Conway는 연산자 abdegjkmost를 정의했다. 이후 구현에서는 추가 연산자를 명명하며, 이를 "확장" 연산자라고도 한다. 콘웨이의 기본 연산은 플라톤의 다면체에서 아르키메데스 다면체와 카탈루냐 다면체를 생성하기에 충분하다. 예를 들어, 두 번 적용되는 앰보는 확장 연산인 aa = e인 반면, 앰보 후 잘라내면 베벨(ta = b)이 생성된다.
다면체는 그들의 꼭짓점, 모서리, 면이 어떻게 서로 연결되는지를 위상적으로 연구하거나 공간에서의 요소 배치의 관점에서 기하학적으로 연구할 수 있다. 이러한 연산자의 다른 구현은 기하학적으로 다르지만 위상적으로 동일한 다면체를 생성할 수 있다. 이러한 위상적으로 동등한 다면체는 구에 다면체 그래프를 많이 내장하는 것으로 생각할 수 있다. 달리 명시되지 않은 한, 본 문서(및 Conway 연산자에 대한 일반적인 문헌)에서는 토폴로지가 주요 관심사이다. 속이 0인 다면체는 모호함을 피하기 위해 종종 정식 형태로 놓이다.
엄정한 활동
편집시드(S), 니들(n), zip(z)은 엄밀히 말하면 존 호턴 콘웨이에서 포함하지 않았지만, 원래 존 호턴 콘웨이 작업과 이중성으로 관련되어 있으므로 여기에 포함된다.
지금부터, 큐브 표면에 그려진 큐브 씨에 대한 작업이 시각화된다. 파란색 면은 씨앗의 가장자리를 가로지르고 분홍색 면은 씨앗의 꼭짓점 위에 놓여 있다. 특히 키랄 연산자의 경우 정점을 정확하게 배치할 때 유연성이 있다.
작업의 확장
편집콘웨이의 원래 세트 이후에 생성된 작업이다. 여기에 작업이 없다고 해서 작업이 존재하지 않거나 LSP 또는 LOPSP가 아니라는 것을 의미하지는 않는다. 단순화하기 위해 이 목록에는 환원 불가능한 연산자만 포함되며 다른 연산자는 연산자를 함께 구성하여 생성할 수 있다.
인덱싱된 확장 작업
편집일부 기준에 따라 여러 연산자를 그룹화하거나 인덱스에 의해 동작이 수정될 수 있다. 이들은n x라는 첨자로 연산자로 기록된다.
확대
편집증강 작업은 원래 가장자리를 유지한다. 그것들은 면의 어떤 독립적인 부분집합에 적용될 수도 있고, 원래의 가장자리를 제거하여 결합 형태로 변환될 수도 있다. 콘웨이 표기법은 이러한 연산자에 대한 선택적 지수를 지원한다. 즉, 결합 양식의 경우 0 또는 영향을 받는 면이 몇 개인지의 경우 3 이상이다. 예를 들어, kY44=O: 정사각형 기반 피라미드를 취하고 다른 피라미드를 정사각형 베이스에 붙이면 8각형이 된다.
| 연산자 | k | l | L | K | (kk) |
|---|---|---|---|---|---|
| x | |||||
| x0 | k0 = j | l0 = c | L0 | K0 = jk | |
| 확대 | 피라미드 | 프리즘 | 향전신병 |
메타/비벨
편집메타는 가운데와 가장자리를 따라 정점을, 베벨은 가운데, 시드 정점, 가장자리를 따라 정점을 추가한다. 지수는 가장자리를 따라 정점 또는 면의 수를 더한 것이다. 메타(비인덱스 형태)는 캔트런지(cantitruncation) 또는 옴니트런지(hunitruncation)라고도 한다. 여기서 0은 확대 연산과 같은 것을 의미하지 않는다는 점에 유의할 것. 즉, 가장자리를 따라 정점(또는 면)이 0으로 추가된다는 것을 의미한다.
| n | 예지 계수 | 메트릭스 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|
| 0 | 3 | k = m0 | n | z = b0 | t | |
| 1 | 6 | m = m1 = kj | b = b1 = ta | |||
| 2 | 9 | m2 | m2d | b2 | b2d | |
| 3 | 12 | m3 | m3d | b3 | b3d | |
| n | 3n+3 | mn | mnd | bn | bnd | |
메디알
편집중심에서 각 시드 정점에 가장자리를 추가하지 않는다는 점을 제외하면 메디알은 메타와 같다. 지수 1 형태는 콘웨이의 정형외과와 확장 연산자와 동일하다. 확장(expansion)은 확장과 확장(cantellation)이라고도 한다. o와 e는 아래에 설명된 자체 인덱싱된 양식을 가지고 있다는 점에 유의할 것. 또한 일부 구현에서는 1이 아닌 0에서 인덱싱을 시작한다는 점에 유의할 것
| n | 가장자리요소 | 메트릭스 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|
| 1 | 4 | M1 = o = jj | e = aa | |||
| 2 | 7 | Medial: M = M2 | Md | dM | dMd | |
| n | 3n+1 | Mn | Mnd | dMn | dMnd | |
골드버그콕시터
편집골드버그-콕세터(GC) 콘웨이 운영자는 골드버그-콕세터 건설의 연장선인 두 무한 연산자 계열이다. GC 구조는 삼각 격자의 삼각형 부분 또는 사각 격자의 사각형 부분을 취하여 다면체의 각 면 위에 놓는 것으로 생각할 수 있다. 이 구조는 삼각형이나 사각형의 챔버("마스터 폴리곤")를 식별하여 어떤 면으로도 확장할 수 있다. 삼각형 계열의 연산자는 Goldberg Polyedra와 Geodesic Polyedra를 생산하는 데 사용될 수 있다: 공식은 Geodesic Polyedra와 Goldberg Polyedra 목록을 참조한다.
두 가문은 삼각형 GC 계열, c와a,b ua,b, 그리고 4각형 GC 계열, e와a,b o이다a,b. 두 GC 패밀리는 두 개의 정수로 지수화된다. 그리고그들은 많은 훌륭한 자질들을 가지고 있다.
- 그 가족의 지수는 복잡한 숫자에 걸쳐 특정한 유클리드 영역과 관계를 가진다: 삼각형 GC 계열의 아이젠슈타인 정수와 4각형 GC 계열의 가우스 정수.
- 같은 가족 내 xxd기둥과 dxd기둥의 운영자들이 서로 통근한다.
운영자는 3가지 등급으로 구분된다(예는 c로 작성되지만 4개 운영자 모두에게 적용).
- 클래스 I:. 아치랄, 원래 가장자리를 보존한다. 0 지수를 억제한 상태로 작성할 수 있다(예a,0: c = ca).
- 클래스 II:. 또한 아치랄. ca,a = cc로a1,1 분해할 수 있음
- 클래스 III: 다른 모든 연산자. 이것들은 치랄이고, c와a,b c는b,a 서로 치랄 쌍이다.
원래 콘웨이 작전 중 GC 계열에 속하지 않는 것은 g와 s(자이로와 스너브)뿐이다. 메타(meta)와 베벨(m과 b)은 삼각형 계열의 연산자 1명과 사각형 계열의 연산자 1명으로 표현할 수 있다.
아르키메데스 다면체와 카탈루냐 다면체
편집- Archimedean
-
깎은 사면체
tT -
정육면체
aC = aaT -
잘린 큐브
tC -
깎은 팔면체
tO = bT -
마름모육팔면체
eC = a3T -
깎은 정육면체
bC -
스너브 큐브
sC -
이십이면체
aD -
깎은 12면체
tD -
깎은 정이십면체
tI -
납작한 십이면체
sD & sI
-
tI=zD
-
atI
-
ttI
-
ztI
-
etI
-
btI
-
stI
- Duals
-
nI=kD
-
jtI
-
ntI
-
ktI
-
otI
-
mtI
-
gtI
-
정사각형 타일링
Q=dQ
-
육각형 타일링
H = dΔ -
삼육각형 타일링
aH = aΔ -
롬비트리헥사각형 타일링
eH = eΔ -
잘린 삼육각형 타일링
bH = bΔ -
삼육각형 타일링
sH = sΔ
-
삼각형 타일링
Δ = dH -
롬빌 타일링
jΔ = jH -
삼각삼각 타일링
oΔ = oH -
키스크롬빌 타일링
mΔ = mH -
플로레 오각형 타일링
gΔ = gH
-
삼각형 타일링
Δ = dH -
롬빌 타일링
jΔ = jH -
삼각삼각 타일링
oΔ = oH -
키스크롬빌 타일링
mΔ = mH -
플로레 오각형 타일링
gΔ = gH