검색 알고리즘
컴퓨터 과학에서 검색 알고리즘(search algorithm)은 이름 그대로 검색 문제를 해결하는 어떠한 알고리즘이라도 해당되며, 연속 변수나 이산 변수를 사용하여, 일부 데이터 구조 안에 저장된 정보를 검색하거나 문제 도메인의 검색 공간에서 계산을 하기 위해 사용된다. 검색 알고리즘이 쓰이는 부문은 다음을 포함한다:
- 조합최적화 문제:
- 차량 경로 문제(VRP): 최단 경로 문제의 일종
- 배낭 문제: 항목들의 집합이 있고 각기 가중치와 값이 있을 때 컬렉션에 포함될 각 항목의 수를 결정함으로써 총 가중치가 주어진 제한과 동등하거나 더 낮게 되고 전체 값이 가능한 크도록 하는 것.
- 너스 스케줄링 문제(nurse scheduling problem)
- 제약식 만족 문제:
- 게임 이론, 특히 조합론적 게임 이론에서 다음 수를 만들기 위해 최상의 수를 선택하기 (예: 최소극대화 알고리즘에서)
- 전체 확률 집합으로부터 조합 또는 비밀번호를 찾아내기
- 정수의 인수분해 (암호학의 중요 문제)
- 프로세스의 변수(온도, 기압, pH 등)를 변경함으로써 이루어지는 산업 과정의 최적화(예: 화학 반응)
- 데이터베이스로부터 레코드 검색
- 리스트나 배열에서 최대값과 최소값 찾기
- 주어진 값이 값 집합에 존재하는지 살펴보기
위의 내용과 웹 검색에 기술되는 고전적인 검색 문제들은 모두 정보 검색의 문제들이지만 일반적으로 별도의 하위 분야로서 연구되며 다르게 해결되고 평가된다. 고전적인 검색 알고리즘들은 일반적으로 얼마나 빨리 해결책을 찾을 수 있는지, 해당 해결책이 최적임을 보장하는지의 여부를 평가한다. 정보 검색 알고리즘이 빨라야 하지만 좋은 결과가 남아있는지, 나쁜 결과가 포함되었는지 등에 대한 순위의 품질이 더 중요하다.
적절한 검색 알고리즘은 검색 대상이 되는 데이터 구조에 따라 달라질 수 있으며 데이터에 관한 이전 지식이 포함될 수도 있다. 일부 데이터베이스 구조는 특히 검색 알고리즘을 더 빠르고 더 효율적으로 만들기 위해 구성되는데, 이를테면 검색 트리, 해시 맵, 데이터베이스 인덱스가 있다.[1][2]
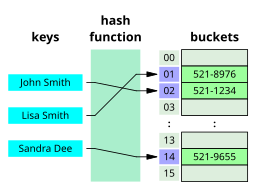
검색 알고리즘은 또한 검색 구조에 따라서도 분류가 가능하다. 순차 검색 알고리즘은 대상 키와 관련된 대상에 대해 모든 레코드를 선형 방식으로 검사한다.[3] 이진/반 정수 검색 알고리즘은 검색 구조의 중심을 대상으로 하고 검색 공간을 절반으로 분리시킨다. 비교 검색 알고리즘은 대상 레코드가 발견될 때까지 키 비교에 기반하여 레코드를 연이어 제거함으로써 선형 검색을 개선시키며, 정의된 순서가 있는 자료 구조에 적용이 가능하다.[4] 디지털 검색 알고리즘은 숫자 키를 사용하는 자료 구조에서 숫자의 속성에 기반하여 동작한다.[5] 끝으로, 해싱(hashing)은 해시 함수에 기반하여 키를 레코드에 직접 매핑시킨다.[6] 선형 검색 밖의 검색은 데이터가 특정 방식으로 정렬될 것이 요구된다.
알고리즘은 자신들만의 계산 복잡도나 이론적 최대 실행 시간에 의해 평가된다. 예를 들어 이진 검색 함수는 O(log n)(또는 로그 함수)의 최대 복잡도를 지닌다. 즉, 검색 대상을 찾는데 필요한 조작의 최대 수는 검색 공간 크기의 로그 함수이다.
같이 보기
편집참고 문헌
편집인용
편집- ↑ Beame & Fich 2002, 39쪽.
- ↑ Knuth 1998, §6.5 ("Retrieval on Secondary Keys").
- ↑ Knuth 1998, §6.1 ("Sequential Searching").
- ↑ Knuth 1998, §6.2 ("Searching by Comparison of Keys").
- ↑ Knuth 1998, §6.3 (Digital Searching).
- ↑ Knuth 1998, §6.4, (Hashing).
서적
편집- Knuth, Donald (1998). 《Sorting and Searching》. The Art of Computer Programming 3 2판. Reading, MA: Addison-Wesley Professional.
문헌
편집- Schmittou, Thomas; Schmittou, Faith E. (2002년 8월 1일). “Optimal Bounds for the Predecessor Problem and Related Problems”. 《Journal of Computer and System Sciences》 65 (1): 38–72. doi:10.1006/jcss.2002.1822.