하이패스 필터

하이패스 필터(High-pass filter, HPF) 또는 고주파 통과 필터는 특정한 차단 주파수 이하 주파수의 신호를 감쇠시켜 차단 주파수 이상의 주파수 신호만 통과시키는 필터를 의미한다. 필터의 세부적인 주파수 응답은 필터 설계에 따라 달라진다. 고주파 통과 필터는 대개 선형 시불변 시스템으로 모델링된다. 이러한 고주파 통과 필터는 종종 오디오 부문에서 저주파 차단 필터(low-cut filter)나 저역 차단 필터(bass-cut filter)라고 부른다. 고주파 통과 필터는 0이 아닌 평균 전압에 민감한 회로나 무선 주파수 장치 같은 곳에서 직류 전압을 차단하는 데 사용하는 등 다양한 분야에 활용된다. 또한 로우패스 필터와 같이 사용하여 대역 필터를 만들 수도 있다.

이상적인 고주파 통과 필터의 주파수 응답 그래프.

광학에서는 "하이 패스"(High-pass)와 "로우 패스"(Low-pass)가 주파수와 빛의 파장 중 어느 쪽에 속하느냐에 따라서 서로 다른 의미를 가질 수 있다. 주파수의 하이 패스 필터(고주파 통과 필터)는 파장의 로우 패스 필터가 되며, 반대로 주파수의 로우 패스 필터(저주파 통과 필터)는 파장의 하이 패스 필터가 될 수 있다. 이 때문에 광학에서 파장 필터는 혼란을 막기 위해 로우 패스/하이 패스 대신 롱 패스(Long-pass), 숏 패스(Short-pass)라고 부른다.

1차 연속시간 회로

수동 아날로그 1차 하이패스 필터를 RC 회로로 구현한 모습.

오른쪽 그림과 같은 간단한 1차 하이패스 필터 회로는 입력 전압에 저항기와 축전기를 직렬로 이어 달고 저항기의 전압을 출력 전압으로 만들어 구현한다. 이 선형 시불변 시스템의 전달 함수는 다음과 같다.

${\frac {V_{\rm {out}}(s)}{V_{\rm {in}}(s)}}={\frac {sRC}{1+sRC}}.$

여기서 저항과 캐패시턴스(정전 용량)의 곱(R×C)이 시간 상수(τ)이며 이는 차단 주파수 f_c와 반비레한다. 즉 아래의 식이 성립한다.

$f_{c}={\frac {1}{2\pi \tau }}={\frac {1}{2\pi RC}},\,$

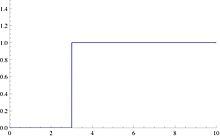
여기서 차단 주파수란 필터의 극점이 필터의 주파수 응답을 벗어나는 시점의 주파수이다. 이보다 낮은 주파수일 경우 그 주파수의 신호는 차단당한다. 위 식을 통해 라플라스 변환 주파수 응답인 $H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}$을 그리면 아래와 같다.

$H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}={s\omega _{0} \over (1+s\omega _{0})}$

능동 하이패스 필터

오른쪽의 능동 하이패스 필터는 연산 증폭기를 사용한 1차 하이패스 필터이다. 여기서의 선형 시불변 시스템 전달 함수는 아래와 같다.

${\frac {V_{\rm {out}}(s)}{V_{\rm {in}}(s)}}={\frac {-sR_{2}C}{1+sR_{1}C}}.$

여기서 필터는 통과 대역에서 -R₂/R₁의 이득을 가지며 차단 주파수는

$f_{c}={\frac {1}{2\pi \tau }}={\frac {1}{2\pi R_{1}C}},\,$

다음과 같다.

이 회로는 능동 회로이므로 필터의 이득이 상수형이 아닐 수 있다. 이 경우 고주파 신호가 반전되고 R₂/R₁만큼 증폭될 수 있다.

이산 시간 해석

이산 시간에서의 하이패스 필터도 생각할 수 있다. 연속 시간 하이패스 필터를 이산 시간으로 샘플링하면 연속시간의 동작을 이산화할 수 있다.

우선, 위 문단에서의 RC 회로에서의 주파수 응답에 키르히호프의 전기회로 법칙과 전기용량를 이용하면 아래와 같다.

${\begin{cases}V_{\text{out}}(t)=I(t)\,R&{\text{(V)}}\\Q_{c}(t)=C\,\left(V_{\text{in}}(t)-V_{\text{out}}(t)\right)&{\text{(Q)}}\\I(t)={\frac {\operatorname {d} Q_{c}}{\operatorname {d} t}}&{\text{(I)}}\end{cases}}$

여기서 $Q_{c}(t)$는 $t$ 시간에 축전지에 충전되어 있는 전하량을 의미한다. 위 식에서 (Q) 식을 (I) 식에, (I) 식을 (V) 식에 대입하여 정리하면 아래와 같다.

$V_{\text{out}}(t)=\overbrace {C\,\left({\frac {\operatorname {d} V_{\text{in}}}{\operatorname {d} t}}-{\frac {\operatorname {d} V_{\text{out}}}{\operatorname {d} t}}\right)} ^{I(t)}\,R=RC\,\left({\frac {\operatorname {d} V_{\text{in}}}{\operatorname {d} t}}-{\frac {\operatorname {d} V_{\text{out}}}{\operatorname {d} t}}\right)$

위 방정식을 이산화시킬 수 있다. 식을 단순하게 풀기 위해 입력 신호와 출력 신호를 일정한 시간 간격인 $\Delta _{T}$마다 샘플링된다고 가정하여 보자. 여기서 샘플링 된 입력 신호 $V_{\text{in}}$는 $(x_{1},x_{2},\ldots ,x_{n})$마다 값이 존재하며 출력 신호 $V_{\text{out}}$는 $V_{\text{out}}$마다 존재하게 샘플링되어 있다. 이를 하나로 묶으면 다음과 같다.

$y_{i}=RC\,\left({\frac {x_{i}-x_{i-1}}{\Delta _{T}}}-{\frac {y_{i}-y_{i-1}}{\Delta _{T}}}\right)$

이 식을 점화식 형태로 만들면 다음과 같다.

$y_{i}=\overbrace {{\frac {RC}{RC+\Delta _{T}}}y_{i-1}} ^{\text{Decaying contribution from prior inputs}}+\overbrace {{\frac {RC}{RC+\Delta _{T}}}\left(x_{i}-x_{i-1}\right)} ^{\text{Contribution from change in input}}$

여기서 1차 연속시간 RC 필터의 이산 시간 구현은 다음으로 적을 수 있다.

$y_{i}=\alpha y_{i-1}+\alpha (x_{i}-x_{i-1})\qquad {\text{where}}\qquad \alpha \triangleq {\frac {RC}{RC+\Delta _{T}}}$

위에서의 정의에 따라 $0\leq \alpha \leq 1$이다. 여기서 변수 $\alpha$를 샘플링 간격 $\Delta _{T}$와의 곱을 통해 시간 상수 $RC$로 만들 수 있다.

$RC=\Delta _{T}\left({\frac {\alpha }{1-\alpha }}\right)$

여기서

$f_{c}={\frac {1}{2\pi RC}}$ so $RC={\frac {1}{2\pi f_{c}}}$

이므로 $\alpha$와 $f_{c}$에는 다음과 같은 관계를 이루게 된다.

$\alpha ={\frac {1}{2\pi \Delta _{T}f_{c}+1}}$

$f_{c}={\frac {1-\alpha }{2\pi \alpha \Delta _{T}}}$

같이 보기

• 로우패스 필터 (LPF)

외부 링크

• Common Impulse Responses
• ECE 209: Review of Circuits as LTI Systems, a short primer on the mathematical analysis of (electrical) LTI systems.
• ECE 209: Sources of Phase Shift, an intuitive explanation of the source of phase shift in a high-pass filter. Also verifies simple passive LPF transfer function by means of trigonometric identity.