기하학 에서 내분 (內分)은 선분 을 그 위의 점을 경계로 하여 두 부분으로 나누는 일이다. 선분을 내분하는 점을 내분점 (內分點)이라고 하며, 나눠진 두 부분의 길이의 비를 내분비 (內分比)라고 한다. 이와 비슷하게, 외분 (外分)은 선분을 그 연장선 위의 점을 경계로 하여 두 부분으로 나누는 일이다. 선분을 외분하는 점을 외분점 (外分點)이라고 하며, 나눠진 두 부분의 길이의 비를 외분비 (外分比)라고 한다.
주어진 내/외분비의 내분점과 외분점의 작도법
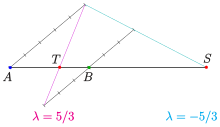
내/외분비의 정의와 예시 세 공선점
A
,
B
,
C
{\displaystyle A,B,C}
A
≠
B
{\displaystyle A\neq B}
내/외분비 (영어 : division ratio )
(
A
,
B
;
C
)
{\displaystyle (A,B;C)}
A
C
→
=
(
A
,
B
;
C
)
C
B
→
{\displaystyle {\overrightarrow {AC}}=(A,B;C){\overrightarrow {CB}}}
즉, 이는 다음과 같다.
(
A
,
B
;
C
)
=
{
|
A
C
|
/
|
C
B
|
B
≠
C
∈
A
B
¯
−
|
A
C
|
/
|
C
B
|
B
≠
C
∉
A
B
¯
∞
^
C
=
B
∈
(
R
∖
{
−
1
}
)
⊔
{
∞
^
}
{\displaystyle (A,B;C)={\begin{cases}|AC|/|CB|&B\neq C\in {\overline {AB}}\\-|AC|/|CB|&B\neq C\not \in {\overline {AB}}\\{\widehat {\infty }}&C=B\end{cases}}\in (\mathbb {R} \setminus \{-1\})\sqcup \{{\widehat {\infty }}\}}
|AB | = 1일 때, t = |AC |와 λ = (A , B ; C )의 관계 λ = t / (1 - t )의 그래프 T 를 ⟶ OA ⟶ OB ⟶ OA ⟶ OB T 의 좌표)는 AB T 의 내분비를 통해 표시할 수 있다.세 점의 위치 관계에 따른 내/외분비의 범위는 다음과 같다.
위치 관계
내/외분비의 범위
C
{\displaystyle C}
A
B
¯
{\displaystyle {\overline {AB}}}
A
{\displaystyle A}
−
1
<
(
A
,
B
;
C
)
<
0
{\displaystyle -1<(A,B;C)<0}
C
=
A
{\displaystyle C=A}
(
A
,
B
;
C
)
=
0
{\displaystyle (A,B;C)=0}
C
{\displaystyle C}
A
{\displaystyle A}
B
{\displaystyle B}
(
A
,
B
;
C
)
>
0
{\displaystyle (A,B;C)>0}
C
{\displaystyle C}
A
B
¯
{\displaystyle {\overline {AB}}}
(
A
,
B
;
C
)
=
1
{\displaystyle (A,B;C)=1}
C
=
B
{\displaystyle C=B}
(
A
,
B
;
C
)
=
∞
^
{\displaystyle (A,B;C)={\widehat {\infty }}}
C
{\displaystyle C}
A
B
¯
{\displaystyle {\overline {AB}}}
B
{\displaystyle B}
(
A
,
B
;
C
)
<
−
1
{\displaystyle (A,B;C)<-1}
또 다른 점
O
{\displaystyle O}
O
C
→
=
1
1
+
(
A
,
B
;
C
)
O
A
→
+
(
A
,
B
;
C
)
1
+
(
A
,
B
;
C
)
O
B
→
{\displaystyle {\overrightarrow {OC}}={\frac {1}{1+(A,B;C)}}{\overrightarrow {OA}}+{\frac {(A,B;C)}{1+(A,B;C)}}{\overrightarrow {OB}}}
내/외분비는 아핀 변환 아래 불변이다. 즉, 아핀 공간 의 공선점
A
,
B
,
C
{\displaystyle A,B,C}
A
≠
B
{\displaystyle A\neq B}
ϕ
{\displaystyle \phi }
ϕ
(
A
)
,
ϕ
(
B
)
,
ϕ
(
C
)
{\displaystyle \phi (A),\phi (B),\phi (C)}
만약
ϕ
(
A
)
≠
ϕ
(
B
)
{\displaystyle \phi (A)\neq \phi (B)}
(
ϕ
(
A
)
,
ϕ
(
B
)
;
ϕ
(
C
)
)
=
(
A
,
B
;
C
)
{\displaystyle (\phi (A),\phi (B);\phi (C))=(A,B;C)}
삼각형 의 무게중심 은 세 중선 의 내분점이며, 세 중선에 대한 무게중심의 내분비는 모두 2이다.좌표 공간 위의 두 점
(
x
1
,
y
1
,
z
1
)
,
(
x
2
,
y
2
,
z
2
)
{\displaystyle (x_{1},y_{1},z_{1}),(x_{2},y_{2},z_{2})}
m
:
n
{\displaystyle m:n}
(
m
x
2
+
n
x
1
m
+
n
,
m
y
2
+
n
y
1
m
+
n
,
m
z
2
+
n
z
1
m
+
n
)
{\displaystyle \left({mx_{2}+nx_{1} \over m+n},{my_{2}+ny_{1} \over m+n},{mz_{2}+nz_{1} \over m+n}\right)}
특히, 이 두 점을 잇는 선분의 중점 의 좌표는 다음과 같다.
(
x
2
+
x
1
2
,
y
2
+
y
1
2
,
z
2
+
z
1
2
)
{\displaystyle \left({x_{2}+x_{1} \over 2},{y_{2}+y_{1} \over 2},{z_{2}+z_{1} \over 2}\right)}
또한, 이 두 점을
m
:
n
{\displaystyle m:n}
(
m
x
2
−
n
x
1
m
−
n
,
m
y
2
−
n
y
1
m
−
n
,
m
z
2
−
n
z
1
m
−
n
)
{\displaystyle \left({mx_{2}-nx_{1} \over m-n},{my_{2}-ny_{1} \over m-n},{mz_{2}-nz_{1} \over m-n}\right)}