방정식

다른 뜻에 대해서는 방정식 (동음이의) 문서를 참고하십시오.

방정식(方程式, 영어: equation)은 미지수의 값에 따라 참, 거짓이 결정되는 등식이다.

1557년 로버트 레코드가 저술한 《기지의 숫돌》에 나오는 등호를 사용한 최초의 방정식. 현대 표기에서의 14x + 15 = 71과 같은 의미이다.

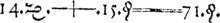
방정식을 참이 되게 하는(성립하게 하는) 미지수의 값을 해(解, solution) 또는 근(根, root)이라 한다. 방정식의 해는 없을 수도 있고, 여러 개일 수도 있고, 모든 값일 수도 있다. 첫 번째의 경우는 불능이라고 하고, 마지막의 경우는 항등식(부정)이라 한다.

예를 들어

$x^{2}-5x+6=0$

은 미지수 $x$의 값에 따라 등식의 참과 거짓이 결정되므로 방정식이고, 그 해는 $2$와 $3$이다. 한편

$(x+1)^{2}=x^{2}+2x+1$

은 문자 $x$가 어떤 값이든 항상 등호가 성립하므로 항등식이다. 그리고

$0\cdot x=2$

는 $x$가 어떤 값이든 항상 등호가 성립하지 못하므로 불능이다.

방정식의 방정(方程)은 고대 중국의 산학서인 구장산술의 여덟 번째 장의 제목인 方程에서 유래하였다. 여기서 方은 연립방정식의 계수를 직사각형 모양으로 배열한다는 뜻이고, 程은 이렇게 배열한 계수를 조작하여 해를 구하는 과정을 뜻한다. 이 해법은 약 1500년 뒤에 등장하는 가우스 소거법에 해당한다. 고대 중국의 수학자들은 이 과정에서 음수의 계산도 자유자재로 할 수 있었다.

방정식에서 미지수를 나타내는 문자로 보통 로마자의 뒤쪽 문자인 $x,y,z$ 등을 사용한다. 이는 프랑스의 수학자 겸 철학자인 르네 데카르트가 시초이다.

방정식은 다양한 종류가 존재한다.

예시

다항 방정식

 이 부분의 본문은 다항식입니다.

이차방정식 x² – x + 2 = 0의 두 근인 -1과 2는 이차 함수 y = x² – x + 2의 그래프가 x축과 만나는 교점이다.

유리수, 실수, 복소수 등 체의 원소를 계수로 가지는 다항식 $P$와 $Q$에 대해

$P=0$ 또는 $P=Q$

로 표현되는 식을 다항 방정식(多項方程式, 영어: polynomial equation) 또는 대수방정식(代數方程式, 영어: algebraic equation))이라고 한다.

차수가 n인 다항식으로 이루어진 다항 방정식을 n차 방정식이라고 한다. 즉 차수가 1인 방정식을 일차 방정식, 2인 방정식을 이차 방정식과 같이 부른다. 예를 들어

$2x+1=3$

은 일차 방정식이고,

$x^{2}-x-2=0$

은 이차 방정식이다.

다항 방정식은 여러 개의 미지수를 가질 수도 있다. 예를 들어

$x^{5}-3x+1=0$

는 미지수가 $x$ 하나인 정수계수 다항 방정식이고,

$y^{4}+{\frac {xy}{2}}={\frac {x^{3}}{3}}-xy^{2}+y^{2}-{\frac {1}{7}}$

는 미지수가 $x,y$ 두 개인 유리수계수 다항 방정식이다.

어떤 유리수계수 다항 방정식은 계수들의 사칙연산과 거듭제곱근만을 이용해 근을 표현할 수 있다. 특히 사차 이하의 다항 방정식은 항상 이러한 방식으로 근을 표현할 수 있다. 즉, 근의 공식이 존재한다. 흔히 근의 공식이라고 하면 이차 방정식의 근의 공식(영어: quadratic formula)을 의미한다. 예를 들어 이차 방정식

$ax^{2}+bx+c=0,(a\neq 0)$

은

$x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}$

을 두 근으로 가지며, 따라서 계수들의 사칙연산과 거듭제곱근만으로 근이 표현된다. 그러나 아벨-루피니 정리에 의하면 오차 이상의 다항방정식은 이러한 방식으로 표현할 수 없는 근이 존재한다.

한편 대수학의 기본 정리에 따르면 모든 복소계수 다항 방정식은 하나 이상의 복소수 근을 가진다.

무리 방정식

방정식의 항에 무리식(루트)을 포함하는 다항식으로 이루어진 방정식을 무리 방정식이라 한다. 예를 들어

$x+{\sqrt {x+1}}-1=0$

는 무리 방정식이다. 위 방정식을 풀면

$x-1=-{\sqrt {x+1}}$

$(x-1)^{2}=(-{\sqrt {x+1}})^{2}$

$(x-1)(x-1)=x+1$

$x^{2}-3x=x(x-3)=0$

가 되어 $x=0,3$이 된다. 그런데 무리 방정식에는 위처럼 유도과정을 거쳐 찾은 값이 방정식에 대입했을 때는 성립하지 않는 무연근이 존재할 수 있다. 따라서 앞에서 얻은 값이 무리방정식의 근이 되는지 검산하는 과정이 필요하다. 예시의 방정식에서 $x=0$을 대입하면 식이 성립하지만, $x=3$을 대입하면 성립하지 않음을 알 수 있다. 따라서 $x=3$은 무연근이고, $x=0$만이 무리 방정식의 근이다.

연립 방정식

연립 방정식은 서로 다른 2개의 미지수가 주어진 방정식들에 모두 적합할 때 이 방정식의 쌍을 의미한다. 연립 방정식도 미지수의 차수에 따라 연립 일차 방정식, 연립 이차 방정식 등으로 나뉜다. 연립 일차 방정식에선 $y=ax+b$와 같이 한 미지수를 어떠한 값으로 나타내어 이 값을 그 미지수에 대입하는 방법인 대입법과 미지수의 계수를 같게 곱하여 둘을 더하거나 빼서 그 미지수를 없애는 가감법, 그리고 행렬을 이용한 가우스 소거법이 주로 사용된다.

미분방정식

 이 부분의 본문은 미분방정식입니다.

오일러 방정식은 유체의 비점성 흐름을 다루는 미분방정식이다.

미분방정식은 함수와 그 도함수들로 표현되는 방정식이다. 일반적으로 어떤 물리적 대상을 표현하는 함수에 대해 그 도함수는 대상의 변화율을 의미하며, 따라서 물리적 대상과 그 변화율 간의 관계는 미분 방정식으로 표현된다. 미분 방정식은 공학, 물리학, 화학, 생물학, 경제학 등 수학 외의 학문에서도 중요한 역할을 차지한다.

상미분방정식

 이 부분의 본문은 상미분방정식입니다.

상미분방정식은 하나의 독립 변수만을 가지는 미분 방정식이다.

편미분방정식

 이 부분의 본문은 편미분방정식입니다.

편미분방정식은 여러 개의 독립 변수를 가지는 미분 방정식이다.

같이 보기

• 디오판토스 방정식
• 다항식
• 수식
• 항등식
• 부등식
• 연립방정식
• 가우스 소거법
• 소거법
• 근 (수학)
• 무연근

외부 링크

• 위키미디어 공용에 방정식 관련 미디어 분류가 있습니다.