정수론 에서 리만 제타 함수 (영어 : Riemann zeta function )
ζ
(
s
)
{\displaystyle \zeta (s)}
소수 들의 정수론 적 성질을 해석 적으로 내포하는 유리형 함수 이다. 해석적 수론 에서 소수 의 분포를 연구할 때 핵심적인 역할을 하며, 또한 L-함수 이론의 모태이다.
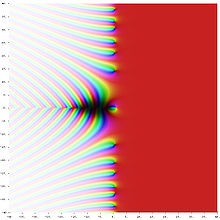
복소평면에서의 리만 제타 함수. 색이 짙을수록 절댓값 이 작으며, 옅을수록 절댓값 이 크다. 색상 은 편각 을 나타내며, 적색은 양의 실수, 연두색은 양의 허수, 옥색은 음의 실수, 남색은 음의 허수를 나타낸다.
야코비 세타 함수
θ
(
τ
)
=
∑
n
=
−
∞
∞
e
π
i
n
2
τ
{\displaystyle \theta (\tau )=\sum _{n=-\infty }^{\infty }e^{\pi in^{2}\tau }}
를 쓰자.
∫
0
∞
e
−
π
n
2
t
t
s
2
d
t
t
=
π
−
s
2
Γ
(
s
2
)
1
n
s
{\displaystyle \int _{0}^{\infty }e^{-\pi n^{2}t}t^{\frac {s}{2}}{\frac {dt}{t}}={\pi }^{-{\frac {s}{2}}}\Gamma ({\frac {s}{2}}){\frac {1}{n^{s}}}}
이므로,
ξ
(
s
)
=
π
−
s
/
2
Γ
(
s
/
2
)
ζ
(
s
)
=
∫
0
∞
(
θ
(
i
t
)
−
1
2
)
t
s
2
d
t
t
{\displaystyle \xi (s)=\pi ^{-s/2}\Gamma (s/2)\zeta (s)=\int _{0}^{\infty }({\frac {\theta (it)-1}{2}})t^{\frac {s}{2}}{\frac {dt}{t}}}
자이 함수(
ξ
{\displaystyle \xi }
[ 1]
s
{\displaystyle s}
s
{\displaystyle s}
ξ
(
s
)
=
1
s
−
1
−
1
s
+
1
2
∫
0
1
(
θ
(
i
t
)
−
1
t
)
t
s
2
d
t
t
+
1
2
∫
1
∞
(
θ
(
i
t
)
−
1
)
t
s
2
d
t
t
{\displaystyle \xi (s)={\frac {1}{s-1}}-{\frac {1}{s}}+{\frac {1}{2}}\int _{0}^{1}(\theta (it)-{\frac {1}{\sqrt {t}}})t^{\frac {s}{2}}{\frac {dt}{t}}+{\frac {1}{2}}\int _{1}^{\infty }(\theta (it)-1)t^{\frac {s}{2}}{\frac {dt}{t}}}
한편 여기서 세타 함수의 성질
θ
(
−
1
τ
)
=
τ
i
θ
(
τ
)
{\displaystyle \theta (-{\frac {1}{\tau }})={\sqrt {\frac {\tau }{i}}}\theta ({\tau })}
를 사용하면,
ξ
(
s
)
=
1
s
−
1
−
1
s
+
1
2
∫
1
∞
(
θ
(
i
t
)
−
1
)
t
1
−
s
2
d
t
t
+
1
2
∫
1
∞
(
θ
(
i
t
)
−
1
)
t
s
2
d
t
t
{\displaystyle \xi (s)={\frac {1}{s-1}}-{\frac {1}{s}}+{\frac {1}{2}}\int _{1}^{\infty }(\theta (it)-1)t^{\frac {1-s}{2}}{\frac {dt}{t}}+{\frac {1}{2}}\int _{1}^{\infty }(\theta (it)-1)t^{\frac {s}{2}}{\frac {dt}{t}}}
를 보일 수 있다.
이로부터 제타 함수의 해석적 연속 과 함수 방정식
ξ
(
s
)
=
ξ
(
1
−
s
)
{\displaystyle \xi (s)=\xi (1-s)}
를 얻는다.
다음은 작은 수에 대한 제타 함수의 값이다.
ζ
(
−
1
)
=
−
1
12
{\displaystyle \zeta (-1)=-{\frac {1}{12}}}
ζ
(
0
)
=
−
1
2
{\displaystyle \zeta (0)=-{\frac {1}{2}}}
ζ
(
1
2
)
≈
−
1.4603545
{\displaystyle \zeta \left({\frac {1}{2}}\right)\approx -1.4603545}
A059750
ζ
(
1
)
=
1
+
1
2
+
1
3
+
⋯
=
∞
{\displaystyle \zeta (1)=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots =\infty }
조화급수 이다.
ζ
(
3
2
)
≈
2.612
;
{\displaystyle \zeta \left({\frac {3}{2}}\right)\approx 2.612;}
A078434 보스-아인슈타인 응축 에서 임계 온도를 계산하는데 사용된다.
ζ
(
2
)
=
1
+
1
2
2
+
1
3
2
+
⋯
=
π
2
6
{\displaystyle \zeta (2)=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}}
A013661 원주율 의 근사값을 구하기 위해 종종 사용된다.
ζ
(
3
)
=
1
+
1
2
3
+
1
3
3
+
⋯
=
1.202
⋯
{\displaystyle \zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+\cdots =1.202\cdots }
A002117 아페리 상수 이다.
ζ
(
4
)
=
1
+
1
2
4
+
1
3
4
+
⋯
=
π
4
90
{\displaystyle \zeta (4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}}
A0013662 플랑크 법칙 으로부터 슈테판-볼츠만 법칙 을 도출하는 적분 과정에서 사용된다.
ζ
(
5
)
=
1
+
1
2
5
+
1
3
5
+
⋯
=
1.036
⋯
{\displaystyle \zeta (5)=1+{\frac {1}{2^{5}}}+{\frac {1}{3^{5}}}+\cdots =1.036\cdots }
ζ
(
6
)
=
1
+
1
2
6
+
1
3
6
+
⋯
=
π
6
945
{\displaystyle \zeta (6)=1+{\frac {1}{2^{6}}}+{\frac {1}{3^{6}}}+\cdots ={\frac {\pi ^{6}}{945}}}
ζ
(
7
)
=
1
+
1
2
7
+
1
3
7
+
⋯
=
1.0083
⋯
{\displaystyle \zeta (7)=1+{\frac {1}{2^{7}}}+{\frac {1}{3^{7}}}+\cdots =1.0083\cdots }
ζ
(
8
)
=
1
+
1
2
8
+
1
3
8
+
⋯
=
π
8
9450
{\displaystyle \zeta (8)=1+{\frac {1}{2^{8}}}+{\frac {1}{3^{8}}}+\cdots ={\frac {\pi ^{8}}{9450}}}
ζ
(
9
)
=
1
+
1
2
9
+
1
3
9
+
⋯
=
1.0020
⋯
{\displaystyle \zeta (9)=1+{\frac {1}{2^{9}}}+{\frac {1}{3^{9}}}+\cdots =1.0020\cdots }
ζ
(
10
)
=
1
+
1
2
10
+
1
3
10
+
⋯
=
π
10
93555
{\displaystyle \zeta (10)=1+{\frac {1}{2^{10}}}+{\frac {1}{3^{10}}}+\cdots ={\frac {\pi ^{10}}{93555}}}
현재 리만 제타 함수가 실수부가 짝수(
2
N
{\displaystyle 2N}
π
2
N
{\displaystyle \pi ^{2N}}
초월수 임이 알려졌다. 홀수일 때에는 3의 제타 함수 값은 무리수이며, 5, 7, 9, 11의 제타 함수 값 중 적어도 하나가 무리수라는 것만이 알려져 있다.
레온하르트 오일러 는 리만 제타 함수가 소수 와 다음과 같은 관계가 있다는 것을 알아냈다.
ζ
(
s
)
=
∏
p
1
1
−
p
−
s
{\displaystyle \zeta (s)=\prod _{p}{\frac {1}{1-p^{-s}}}}
ζ
(
s
)
(
1
−
1
2
s
)
(
1
−
1
3
s
)
(
1
−
1
5
s
)
⋯
=
1
{\displaystyle \zeta (s)\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\cdots =1}
위와 같은 절차를 거쳐서 우변의 모든 소수의 배수를 없애주면
특정 합성수는 항상 소수의 곱으로써 나타낼 수 있다는 산술의 기본 정리 에 따라서 분모가 합성수 또는 소수인 수가 모두 사라지고
마지막에는 1만이 남는다. 즉
ζ
(
s
)
∏
p
(
1
−
1
p
s
)
=
1
{\displaystyle \zeta (s)\prod _{p}\left(1-{1 \over {p^{s}}}\right)=1}
ζ
(
s
)
∏
p
(
1
−
p
−
s
)
=
1
{\displaystyle \zeta (s)\prod _{p}\left(1-p^{-s}\right)=1}
∴
ζ
(
s
)
=
∏
p
1
1
−
p
−
s
{\displaystyle \therefore \;\zeta (s)=\prod _{p}{\frac {1}{1-p^{-s}}}}
위에서 제시되는,
ζ
(
s
)
=
1
1
s
+
1
2
s
+
1
3
s
+
⋯
{\displaystyle \zeta (s)={1 \over 1^{s}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots }
ζ
(
s
)
=
1
1
s
+
1
2
s
+
1
3
s
+
⋯
=
∑
n
=
1
∞
1
n
s
=
ζ
(
s
)
{\displaystyle \zeta (s)={1 \over 1^{s}}+{{1} \over {2^{s}}}+{{1} \over {3^{s}}}+\cdots =\sum _{n=1}^{\infty }{{1} \over {n^{s}}}=\zeta (s)}
이것은 디리클레 급수 (디리클레 덧셈)이다.
따라서,
ζ
(
s
)
=
∑
n
=
1
∞
1
n
s
=
∏
p
1
1
−
p
−
s
{\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{{1} \over {n^{s}}}=\prod _{p}{\frac {1}{1-p^{-s}}}}
리만 제타 함수는 규칙적으로 모든 자연수에 대한 무한급수로 정의되어 있기 때문에 많은 방법으로 성질을 탐구할 수 있다. 그리고 이 리만 제타 함수는 오일러 곱을 통해 소수와 연결된다. 따라서, 이 식을 이용하면 소수의 비밀을 수학적으로 파헤칠 수 있으며, 그렇기 때문에 이 식은 중요하게 이용된다.
즉 리만 제타 함수는 모든 소수
p
{\displaystyle p}
오일러의 곱셈 공식 이라 불리며, 등비급수 의 식과 산술의 기본 정리 로부터 유도해낼 수 있다. 그 간단한 증명은 다음과 같다.
ζ
(
s
)
=
1
1
s
+
1
2
s
+
1
3
s
+
⋯
{\displaystyle \zeta (s)={1 \over 1^{s}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots }
ζ
(
s
)
=
1
+
1
2
s
+
1
3
s
+
⋯
{\displaystyle \zeta (s)=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots }
1
2
s
{\displaystyle {1 \over 2^{s}}}
1
2
s
⋅
ζ
(
s
)
=
1
(
2
⋅
1
)
s
+
1
(
2
⋅
2
)
s
+
1
(
2
⋅
3
)
s
+
1
(
2
⋅
4
)
s
+
⋯
{\displaystyle {1 \over 2^{s}}\cdot \zeta (s)={1 \over (2\cdot 1)^{s}}+{1 \over (2\cdot 2)^{s}}+{1 \over (2\cdot 3)^{s}}+{1 \over (2\cdot 4)^{s}}+\cdots }
1
2
s
{\displaystyle {1 \over 2^{s}}}
ζ
(
s
)
−
(
1
2
s
⋅
ζ
(
s
)
)
=
1
+
1
3
s
+
1
5
s
+
1
7
s
+
⋯
{\displaystyle \zeta (s)-\left({\frac {1}{2^{s}}}\cdot \zeta (s)\right)=1+{\frac {1}{3^{s}}}+{\frac {1}{5^{s}}}+{\frac {1}{7^{s}}}+\cdots }
ζ
(
s
)
(
1
−
1
2
s
)
=
1
+
1
3
s
+
1
5
s
+
1
7
s
+
⋯
{\displaystyle \zeta (s)\left(1-{\frac {1}{2^{s}}}\right)=1+{\frac {1}{3^{s}}}+{\frac {1}{5^{s}}}+{\frac {1}{7^{s}}}+\cdots }
우변의 분모에서 2의 배수가 모두 사라지는 것을 관찰할 수 있다. 또한 계속해서 반복하면,
ζ
(
s
)
(
1
−
1
2
s
)
(
1
−
1
3
s
)
=
1
+
1
5
s
+
1
7
s
+
1
11
s
+
⋯
{\displaystyle \zeta (s)\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)=1+{\frac {1}{5^{s}}}+{\frac {1}{7^{s}}}+{\frac {1}{11^{s}}}+\cdots }
동일한 절차로 우변의 분모에서 3의 배수가 모두 사라진다.
함수 방정식에 따라, 리만 제타 함수는 음의 짝수
s
=
−
2
,
−
4
,
−
6
,
…
{\displaystyle s=-2,-4,-6,\dots }
자명한 영점 (영어 : trivial zero )이라고 한다. 리만 제타 함수의 자명하지 않은 영점들은 다음과 같은 임계 구역 (영어 : critical strip )에 존재한다.
{
s
∈
C
:
0
<
Re
s
<
1
}
{\displaystyle \{s\in \mathbb {C} \colon 0<\operatorname {Re} s<1\}}
임계 구역에서 다음과 같은 부분집합을 임계 직선 (영어 : critical line )이라고 한다.
{
s
∈
C
:
Re
s
=
1
/
2
}
{\displaystyle \{s\in \mathbb {C} \colon \operatorname {Re} s=1/2\}}
임계 직선 위에는 무한히 많은 영점들이 존재한다는 사실이 알려져 있다. 현재까지 계산된 모든 비자명 영점들은 임계 직선 위에 존재하고 있지만, 모든 영점들이 실제로 임계 직선 위에 있는지 여부는 아직 증명되거나 반증되지 못했다. 이는 리만 가설
리만 제타 함수의 영점들은 해석적 수론 에서 소수 의 분포에 대한 연구에 대해 매우 중요한 역할을 한다. 예를 들어, 소수 정리 는 리만 제타 함수의 영점들에 대한 동치인 명제로 바뀌어 증명될 수 있다.
리만 제타 함수를 일반화한 몇 가지 제타 함수 가 있다. 그중 가장 간단한 것은 후르비츠 제타 함수 이며 다음과 같이 정의된다.
ζ
(
s
,
q
)
=
∑
k
=
0
∞
(
k
+
q
)
−
s
{\displaystyle \zeta (s,q)=\sum _{k=0}^{\infty }(k+q)^{-s}}
이 함수는
q
=
1
{\displaystyle q=1}