정이십면체
| 정이십면체 | |
|---|---|
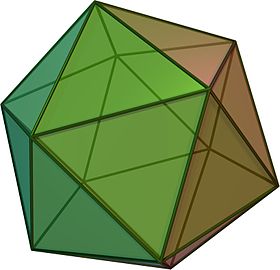 (클릭해서 회전하는 모델을 볼 수 있다) | |
| 종류 | 플라톤 다면체 |
| 성분 | F = 20, E = 30 V = 12 (χ = 2) |
| 면의 수{변의 수} | 20{3} |
| 콘웨이 표기 | I sT |
| 슐레플리 기호 | {3,5} |
| s{3,4} sr{3,3} or | |
| 면 배치 | V5.5.5 |
| 위토프 기호 | 5 | 2 3 |
| 콕서터 다이어그램 | |
| 대칭 | Ih, H3, [5,3], (*532) |
| 회전군 | I, [5,3]+, (532) |
| 참조 | U22, C25, W4 |
| 특성 | 정다면체, 볼록델타다면체 |
| 이면각 | 138.189685° = arccos(−√53) |
 3.3.3.3.3 (꼭짓점 도형) |
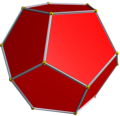 정십이면체 (쌍대 다면체) |
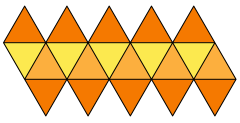 전개도 | |
(正二十面體, 영어: Icosahedron)는 한 개의 에 다섯 개의 면이 만나고, 20개의 정삼각형 면으로 이루어진 3차원 정다면체이다. 모서리의 수는 30개, 꼭짓점의 수는 12개이다.

아데노바이러스를 비롯하여, 많은 종류의 바이러스들이 정이십면체 모양이다.
정십이면체와 쌍대다면체이다. 또 정이십면체는 비틀어 늘린 오각쌍뿔로 생각해도 될 정도이고 윗부분은 오각뿔이며, 오각쌍뿔 사이에 엇정오각기둥을 끼워 넣어서 만들 수 있다.
그리고 정팔면체의 모서리를 쐐기꼴로 배치해서 만들 수도 있으므로 다듬은 정팔면체라고도 한다. 이면각의 크기는 약 138.19°이므로 한 모서리에 정이십면체 3개가 모이면 약 414.57°로 360°를 초과하기 때문에 볼록한 4차원 정다포체를 만들 수 없다.
물론 그렇다 하더라도 정이십면체 5개를 별모양으로 교차해서 만나게 하여 한 모서리에 (이분의 오)개가 모이게 해준다면 정이십면체 백이십포체라는 4차원 오목 정다포체를 만들 수 있다. 두 곳은 마주보게 자르면 엇오각기둥이 되는다는 것을 이용해 엇정오각기둥의 경우 이면각의 크기를 측정해 보면 각각 3_3:138.17°, 3_5:104.75° (p_q는 p각형과 q각형이 만나는 모서리 사이의 이면각의 크기다) 라는 것을 알 수 있다.
공식
편집한 모서리의 길이가 인 정이십면체의 부피와 겉넓이는 다음과 같다.
| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |

