상집합(商集合)에 대해서는
몫집합 문서를 참고하십시오.
순서론 에서 상집합 (上集合, 영어 : upper set , upward-closed set , upset )은
S
{\displaystyle S}
S
{\displaystyle S}
원순서 집합 의 부분 집합
S
{\displaystyle S}
하집합 (下集合, 영어 : lower set , downward-closed set , downset )은
S
{\displaystyle S}
S
{\displaystyle S}
원순서 집합 의 부분 집합
S
{\displaystyle S}
집합
{
1
,
2
,
3
,
4
}
{\displaystyle \{1,2,3,4\}}
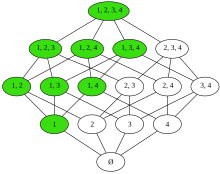
부분 집합 이 부분 순서 로 나열되어 있다. 원소 1을 포함하는 모든 집합(녹색)은 상집합이며, 이는 추가로 필터 를 이룬다.
원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
부분 집합
S
⊆
X
{\displaystyle S\subseteq X}
상폐포 (上閉包, 영어 : upper closure )는 다음과 같은 부분 집합 이다.
↑
S
=
{
x
∈
X
:
∃
s
∈
S
:
s
≲
x
}
{\displaystyle \uparrow S=\{x\in X\colon \exists s\in S\colon s\lesssim x\}}
이는
S
{\displaystyle S}
원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
부분 집합
S
⊆
X
{\displaystyle S\subseteq X}
하폐포 (下閉包, 영어 : lower closure )는 다음과 같은 부분 집합 이다.
↓
S
=
{
x
∈
X
:
∃
s
∈
S
:
x
≲
s
}
{\displaystyle \downarrow S=\{x\in X\colon \exists s\in S\colon x\lesssim s\}}
이는
S
{\displaystyle S}
원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
부분 집합
S
⊆
X
{\displaystyle S\subseteq X}
동치 이며, 이를 만족시키는 부분 집합 을 상집합 (上集合, 영어 : upper set )이라고 한다.
임의의
x
∈
S
{\displaystyle x\in S}
y
∈
X
{\displaystyle y\in X}
x
≲
y
{\displaystyle x\lesssim y}
y
∈
S
{\displaystyle y\in S}
↑
S
⊆
S
{\displaystyle \uparrow S\subseteq S}
↑
S
=
S
{\displaystyle \uparrow S=S}
s
∈
S
{\displaystyle s\in S}
사슬
C
⊆
X
{\displaystyle C\subseteq X}
{
s
}
=
min
C
{\displaystyle \{s\}=\min C}
C
⊆
S
{\displaystyle C\subseteq S}
X
∖
S
{\displaystyle X\setminus S}
원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
부분 집합
S
⊆
X
{\displaystyle S\subseteq X}
동치 이며, 이를 만족시키는 부분 집합 을 하집합 (下集合, 영어 : lower set )이라고 한다.
임의의
x
∈
S
{\displaystyle x\in S}
y
∈
X
{\displaystyle y\in X}
y
≲
x
{\displaystyle y\lesssim x}
y
∈
S
{\displaystyle y\in S}
↓
S
⊆
S
{\displaystyle \downarrow S\subseteq S}
↓
S
=
S
{\displaystyle \downarrow S=S}
s
∈
S
{\displaystyle s\in S}
사슬
C
⊆
X
{\displaystyle C\subseteq X}
{
s
}
=
max
C
{\displaystyle \{s\}=\max C}
C
⊆
S
{\displaystyle C\subseteq S}
X
∖
S
{\displaystyle X\setminus S}
원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
(
U
i
)
i
∈
I
{\displaystyle (U_{i})_{i\in I}}
교집합
⋂
i
∈
I
U
i
{\displaystyle \bigcap _{i\in I}U_{i}}
및 합집합
⋃
i
∈
I
U
i
{\displaystyle \bigcup _{i\in I}U_{i}}
역시 상집합이다. 마찬가지로, 하집합들의 (유한 또는 무한) 족의 교집합 과 합집합 역시 하집합이다.
따라서, 원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
부분 집합 관계에 대하여) 완비 격자 를 이룬다. 마찬가지로,
(
X
,
≤
)
{\displaystyle (X,\leq )}
완비 격자 를 이룬다.
부분 순서 집합
(
X
,
≤
)
{\displaystyle (X,\leq )}
U
⊆
X
{\displaystyle U\subseteq X}
극소 원소 들의 집합
min
U
{\displaystyle \min U}
X
{\displaystyle X}
반사슬 을 이룬다. 마찬가지로,
(
X
,
≤
)
{\displaystyle (X,\leq )}
L
⊆
X
{\displaystyle L\subseteq X}
극대 원소 들의 집합
max
L
{\displaystyle \max L}
X
{\displaystyle X}
반사슬 을 이룬다.
반대로, 부분 순서 집합
(
X
,
≤
)
{\displaystyle (X,\leq )}
반사슬
A
⊆
X
{\displaystyle A\subseteq X}
↑
A
{\displaystyle \uparrow A}
min
↑
A
=
A
{\displaystyle \min \uparrow A=A}
max
↓
A
=
A
{\displaystyle \max \downarrow A=A}
이다. 따라서,
X
{\displaystyle X}
반사슬 집합에서 상집합 집합으로 가는 함수
↑
:
Antichain
(
X
,
≤
)
→
Upper
(
X
,
≤
)
{\displaystyle \uparrow \colon \operatorname {Antichain} (X,\leq )\to \operatorname {Upper} (X,\leq )}
는 단사 함수 이며,
max
:
Upper
(
X
,
≤
)
→
Antichain
(
X
,
≤
)
{\displaystyle \max \colon \operatorname {Upper} (X,\leq )\to \operatorname {Antichain} (X,\leq )}
는 그 왼쪽 역사상 이자 전사 함수 이다.
만약
(
X
,
≤
)
{\displaystyle (X,\leq )}
내림 사슬 조건 을 만족시킨다면 이 두 함수는 전단사 함수 이다. 그러나 일반적 부분 순서 집합 에 대해서는 전단사 함수 가 아닐 수 있다. 예를 들어, 실수 의 전순서 집합 에서 양의 실수의 부분 집합
R
+
⊆
R
{\displaystyle \mathbb {R} ^{+}\subseteq \mathbb {R} }
극소 원소 를 갖지 않는다.
임의의 원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
X
{\displaystyle X}
공집합
∅
⊆
X
{\displaystyle \varnothing \subseteq X}
X
{\displaystyle X}
임의의 원순서 집합
(
X
,
≲
)
{\displaystyle (X,\lesssim )}
x
∈
X
{\displaystyle x\in X}
↑
{
x
}
=
{
y
∈
X
:
x
≲
y
}
{\displaystyle \uparrow \{x\}=\{y\in X\colon x\lesssim y\}}
↓
{
x
}
=
{
y
∈
X
:
y
≲
x
}
{\displaystyle \downarrow \{x\}=\{y\in X\colon y\lesssim x\}}
는 각각 상집합과 하집합을 이룬다. 사실, 이들은 각각 필터 와 아이디얼 을 이룬다.
실수의 전순서 집합
(
R
,
≤
)
{\displaystyle (\mathbb {R} ,\leq )}
(
a
,
∞
)
{\displaystyle (a,\infty )}
a
∈
R
{\displaystyle a\in \mathbb {R} }
[
a
,
∞
)
{\displaystyle [a,\infty )}
a
∈
R
{\displaystyle a\in \mathbb {R} }
R
{\displaystyle \mathbb {R} }
∅
{\displaystyle \varnothing }
마찬가지로, 실수의 전순서 집합
(
R
,
≤
)
{\displaystyle (\mathbb {R} ,\leq )}
(
−
∞
,
a
)
{\displaystyle (-\infty ,a)}
a
∈
R
{\displaystyle a\in \mathbb {R} }
(
−
∞
,
a
]
{\displaystyle (-\infty ,a]}
a
∈
R
{\displaystyle a\in \mathbb {R} }
R
{\displaystyle \mathbb {R} }
∅
{\displaystyle \varnothing }
순서수 는 스스로 미만의 다른 순서수 들의 집합으로 여길 수 있다.
α
=
{
β
∈
Ord
:
β
<
α
}
{\displaystyle \alpha =\{\beta \in \operatorname {Ord} \colon \beta <\alpha \}}
이 경우, 두 순서수
α
,
β
{\displaystyle \alpha ,\beta }
α
≤
β
{\displaystyle \alpha \leq \beta }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
순서수
α
{\displaystyle \alpha }
{
β
∈
Ord
:
β
0
≤
β
<
α
}
{\displaystyle \{\beta \in \operatorname {Ord} \colon \beta _{0}\leq \beta <\alpha \}}
β
0
≤
α
+
1
{\displaystyle \beta _{0}\leq \alpha +1}
순서수
α
{\displaystyle \alpha }
{
β
∈
Ord
:
β
<
β
0
}
{\displaystyle \{\beta \in \operatorname {Ord} \colon \beta <\beta _{0}\}}
β
0
≤
α
+
1
{\displaystyle \beta _{0}\leq \alpha +1}
상집합(商集合)에 대해서는 몫집합 문서를 참고하십시오.
이 부분의 본문은 필터 (수학)입니다.
![{\displaystyle (-\infty ,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeced831f088e701d1985fb783959d2309e0d32a)
