삼차 방정식 이란 최고차항의 차수가 3인 다항식 을 뜻하며, 일반적인 방정식 형태는 다음과 같다.
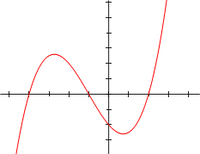
삼차 함수 의 그래프
a
x
3
+
b
x
2
+
c
x
+
d
=
0
,
a
≠
0
{\displaystyle ax^{3}+bx^{2}+cx+d=0,a\neq 0}
여기에서
a
,
b
,
c
{\displaystyle a,b,c}
x
3
,
x
2
,
x
{\displaystyle x^{3},x^{2},x}
계수 라고 하며,
d
{\displaystyle d}
상수항 이다.
고대 바빌로니아 에서는, 수표를 이용하여 3차 방정식의 근을 어느 정도의 근사치로서 구할 수 있었다.
또한 고대 그리스 에서는 키오스의 히포크라테스 에 의해서
p
{\displaystyle p}
q
{\displaystyle q}
p : x = x : y = y : q 되는 수 x , y 을 요구한다고 하는 비 의 문제인 입방 배적 문제 로 알려져 있다. 입방 배적 문제 는 3대 작도 문제 중 1개이다.
메나이크모스 는 히포크라테스의 아이디어로부터 원추 곡선 을 생각해 내어 입방 배적 문제를 원추곡선에 의한 작도에 의해서 풀어내었다. 메나이크모스는 이 업적으로 인하여 원추 곡선의 발견자라고 알려져 있다. 입방 배적 문제는
x 3 = 2 p 3 (p > 0)
의 형태의 3차 방정식을 푸는 것과 같고 메나이크모스에 의한 방법은, 3차 방정식의 기하학적 해법 중 1개로 생각 할 수 있어서 원추 곡선의 표를 계산해 두면 3차 방정식의 근의 근사치도 알 수 있게 된다. 그러나 일반적으로 원추 곡선은 플라톤의 작도 아래에서도 작도할 수 있다. 곡선 은 아니기 때문에 원추 곡선에 의한 기하학적 해법은 입방 배적 문제의 해법으로 보이지는 않는다.
이러한 원추 곡선의 연구는 아르키메데스 나 이븐 알 하이탐 등을 거쳐, 셀주크 제국 시대 페르시아 의 오마르 하이얌 에 의해 확장되어 여러 가지 형태를 취한 3차방정식의 근이 원추 곡선끼리의 교점으로서
삼차방정식의 대수적 해법 은 16세기 무렵에 볼로냐 대학 의 시피오 델 페로 가 발견한 것으로 여겨지고 있다.[출처 필요 ]
x 3 + a 1 x = a 0 (a 1 및 a 0 은 음수 )이런 형태의 공식이다. 당시에는 음수는 인정되지 않았기 때문에 계수 는 아주 한정되어 있었다.
이 방정식 자체는 특수한 형태이지만, 일반적인 3차 방정식은 이 형태로 변형할 수 있기 때문에, 본질적으로는 3차 방정식은 델 페로가 풀었다고 해도 과언은 아니다. 또한 이 방정식의 경우는 계수의 부호의 제약으로부터 환원 불능이 되지 않는다.
델 페로는 이 해법을 공개하지 않고, 제자 몇 명에게만 알려준 뒤 1526년 에 죽었다. 그리고 그 제자 중의 한 명인 안토니아 마리아 피올 (Antonio Maria Fior)은 이 방법을 이용하여 당시에 성행했던 금전을 건 계산 승부에서 계속 이겼다.
3차 방정식의 해답이 있다고 하는 소문을 바탕으로 타르탈리아 (Tartaglia)는 독자적인 힘인지는 몰라도
x 3 + a 2 x 2 = a 0 (a 2 및 a 0 는 정수)의 형태의 3차 방정식을 푸는 것에 성공한 뒤 델·페로의 3차 방정식의 해법도 알아냈다. 타르탈리아가 3차 방정식을 풀었다는 소문을 들은 피올은 소문을 믿지 않고 타르탈리아에게 계산 승부에서 패배시켜 자신의 명성을 올리려고 하였지만, 델·페로의 3차 방정식의 해법 밖에 몰랐기 때문에 피올은 타르탈리아와의 승부에서 지게 된다.
타르탈리아가 3차 방정식의 대수적 해법을 알고 있다고 듣게 된 카르다노 는 타르탈리아에게 간절히 부탁을 하여 3차 방정식의 해법을 알아냈다. 카르다노는 제자인 로도비코 페라리 와 얻은, 일반적인 사차 방정식 의 대수적 해법과 아울러, 3차 방정식의 대수적 해법을 출판하고 싶다고 생각했지만, 타르탈리아에게 해법을 비밀에 붙인다고 맹세했기 때문에 출판할 수는 없었다.
거기서, 일찍이 델 페로가 3차방정식의 대수적 해법을 얻었다고 하는 소문을 믿고 페라리와 볼로냐 에 가서, 델 페로의 양자인 안니바레 델라 나베 를 만나 델 페로의 유고를 보고 그것을 읽은 카르다노는 타르탈리아가 3차방정식을 푼 최초의 사람이 아닌 것을 알았으므로, 타르탈리아와의 약속을 무효화 시켜 1545년에 수학,철학,의학의 내용을 담는 《아르스 마그나[ 1]
이에, 3차 방정식의 해법은 “카르다노의 방법”으로도 불리게 되었다. 이 일은 타르탈리아를 격노시켜 논쟁으로 발전했지만, 카르다노는 《아르스 마그나》에서 델 페로와 타르탈리아의 공적에 대해 칭찬하고 있어, 3차 방정식의 해법이 카르다노 자신의 독자적인 방법이라고 속인 것은 아니다. 또한 타르탈리아로부터 해의 도출 방법까지는 묻지 않고 다양한 형태의 3차 방정식에 대한 해를 나타낸 일은 카르다노 자신의 업적이다.
일반적으로, 일변수의 3차 방정식은
a
3
x
3
+
a
2
x
2
+
a
1
x
+
a
0
=
0
(
a
3
≠
0
)
{\displaystyle a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=0(a_{3}\neq 0)}
의 형태로 표현된다. 현대에서의 3차 방정식의 해법이라고 하면, 주로 대수적 해법의 일을 의미한다.
고대 바빌로니아에서 이미 대수적으로 풀려 있었다고 생각되는 2차 방정식과 달리, 3차 방정식이 대수적으로 풀린 것은 16세기가 되고 나서이다. 11세기 무렵 원추 곡선에 의한 작도에 의해서 3차 방정식의 근을 기하학적으로 나타냈다 오마르 하이얌 도, 3차 방정식을 대수적으로 풀 수 없다고 생각하고 있었다.
3차 방정식의 대수적 해법은 갈루아 이론으로 도달하는 대수방정식론의 시작이며 카르다노의 저서 「아르스 마그나」에 의해서 3차 방정식과 4차 방정식의 대수적 해법을 공표했다. 1545년은 이 공표로 인하여 현대 수학자들에게 수학 시작의 해로 여겨지고 있다.
아직 음수가 수학자들에게 별로 받아 들여지지 않았던 시대이며 모든 계수가 정수이다고 하여 다루어졌기 때문에 예를 들면,
x
3
=
a
1
x
+
a
0
{\displaystyle x^{3}=a_{1}x+a_{0}}
x
3
+
a
1
x
=
a
0
{\displaystyle x^{3}+a_{1}x=a_{0}}
의 2개의 3차 방정식은, 모두 2차항이 없는 3차 방정식이지만, 다른 형태의 방정식으로 여겨졌다.
이와 같이, 음수조차 기피되던 시대에, 3차 방정식의 대수적 해법은 허수 를 가져왔다. 3차 방정식의 근이 모두 정수인 경우에 한해서도, 대수적 해법을 고집하는 한 허수를 피하고는 통과할 수 없는 것이다. 허수에 대한 불안은 19세기에 오귀스탱 루이 코시 나 카를 프리드리히 가우스 가 활약하게 될 때까지 계속되었다.
또, 3차 방정식과 4차 방정식의 대수적 해법의 발견을 바탕으로 수학자들은 5차 이상의 일반의 대수방정식의 대수적 해법을 추구했다. 최종적으로, 이 대수적 해법의 존재는 아벨-르피니의 정리 에 의해서 부정되지만, 갈루아 이론 으로서 결과로 군 이나 체 등의, 기본적인 대수적 구조의 개념을 낳았다.
삼차방정식에서 실근은 '서로 다른 실근 3개', '서로 다른 실근 2개 (하나는 이중근)', '실근 하나'와 같은 경우가 존재한다. 여기서 근의 개수가 몇 개인지를 알아보고자 할 때, 삼차방정식을 미분하여 생긴 이차방정식을 분석함으로써 이를 알아낼 수 있다.
삼차방정식
f
(
x
)
=
0
{\displaystyle f(x)=0}
d
d
x
f
(
x
)
=
a
x
2
+
b
x
+
c
{\displaystyle {\frac {d}{dx}}f(x)=ax^{2}+bx+c}
이차함수의 판별식
D
=
b
2
−
4
a
c
{\displaystyle D=b^{2}-4ac}
D
>
0
{\displaystyle D>0}
d
d
x
f
(
x
)
=
0
{\displaystyle {\frac {d}{dx}}f(x)=0}
α
,
β
{\displaystyle \alpha ,\beta }
f
(
α
)
f
(
β
)
>
0
{\displaystyle f(\alpha )f(\beta )>0}
f
(
α
)
f
(
β
)
=
0
{\displaystyle f(\alpha )f(\beta )=0}
f
(
α
)
f
(
β
)
<
0
{\displaystyle f(\alpha )f(\beta )<0}
D
=
0
{\displaystyle D=0}
d
d
x
f
(
x
)
=
0
{\displaystyle {\frac {d}{dx}}f(x)=0}
γ
{\displaystyle \gamma }
f
(
γ
)
=
0
{\displaystyle f(\gamma )=0}
f
(
γ
)
≠
0
{\displaystyle f(\gamma )\neq 0}
D
<
0
{\displaystyle D<0}
이 방법 이외로도 삼차방정식의 판별식
x
3
+
p
x
+
q
=
0
,
Δ
=
−
4
p
3
−
27
q
2
{\displaystyle x^{3}+px+q=0,\Delta =-4p^{3}-27q^{2}}
x
3
+
b
a
x
2
+
c
a
x
+
d
a
=
0
,
Δ
=
−
4
c
3
+
c
2
b
2
−
27
d
2
+
18
b
c
d
−
4
b
3
d
{\displaystyle x^{3}+{b \over a}x^{2}+{c \over a}x+{d \over a}=0,\Delta =-4c^{3}+c^{2}b^{2}-27d^{2}+18bcd-4b^{3}d}
a
x
3
+
b
x
2
+
c
x
+
d
=
0
,
Δ
=
b
2
c
2
−
4
a
c
3
−
4
b
3
d
−
27
a
2
d
2
+
18
a
b
c
d
{\displaystyle ax^{3}+bx^{2}+cx+d=0,\Delta =b^{2}c^{2}-4ac^{3}-4b^{3}d-27a^{2}d^{2}+18abcd}
위 삼차방정식의 판별식
Δ
{\displaystyle \Delta }
[ 2]
Δ
>
0
{\displaystyle \Delta >0}
Δ
=
0
{\displaystyle \Delta =0}
(만약
9
a
b
c
=
2
b
3
+
27
a
2
d
{\displaystyle 9abc=2b^{3}+27a^{2}d}
Δ
<
0
{\displaystyle \Delta <0}
또한, 실베스터 행렬 식
(#카르다노의 해법 과 판별식 을 참조)
일반적인 3차 방정식의 대수적 해법은 카르다노의 방법 혹은 카르다노의 공식으로 알려져 있다. 스키피오 델 페로 (Scipione del Ferro) 및 니콜로 폰타나 타르탈리아 (Niccolo Fontana Tartaglia)가 먼저 주요한 발견을 한 것으로 알려져있다.
a
3
x
3
+
a
2
x
2
+
a
1
x
+
a
0
=
0
{\displaystyle a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=0}
(
a
3
≠
0
)
{\displaystyle (a_{3}\neq 0)}
을
a
3
{\displaystyle a_{3}}
x
3
+
A
2
x
2
+
A
1
x
+
A
0
=
0
{\displaystyle x^{3}+A_{2}x^{2}+A_{1}x+A_{0}=0}
의 형태로 만든다. 다만
A
n
=
a
n
a
3
{\displaystyle A_{n}={\frac {a_{n}}{a_{3}}}}
x
=
y
−
A
2
3
{\displaystyle x=y-{A_{2} \over 3}}
에 의해서 변수 변환을 실시하면
y
3
+
(
A
1
−
A
2
2
3
)
y
+
(
A
0
−
1
3
A
1
A
2
+
2
27
A
2
3
)
=
0
{\displaystyle y^{3}+\left(A_{1}-{A_{2}^{2} \over 3}\right)y+\left(A_{0}-{1 \over 3}A_{1}A_{2}+{2 \over 27}A_{2}^{3}\right)=0}
와 같이 2차항이 사라진 방정식을 얻을 수 있다. 보기 쉽게 일차의 계수를 p, 상수항을 q로 하여서
y
3
+
p
y
+
q
=
0
{\displaystyle y^{3}+py+q=0}
이라고 쓴다. 한층 더
y
=
u
+
v
{\displaystyle y=u+v}
라고 두면
(
u
+
v
)
3
+
p
(
u
+
v
)
+
q
=
0
{\displaystyle (u+v)^{3}+p(u+v)+q=0}
이것은 정리하면,
u
3
+
v
3
+
q
+
(
3
u
v
+
p
)
(
u
+
v
)
=
0
{\displaystyle u^{3}+v^{3}+q+(3uv+p)(u+v)=0}
여기서
u
3
+
v
3
+
q
=
0
{\displaystyle u^{3}+v^{3}+q=0}
3
u
v
+
p
=
0
{\displaystyle 3uv+p=0}
u
3
+
v
3
+
q
+
(
3
u
v
+
p
)
(
u
+
v
)
=
0
{\displaystyle u^{3}+v^{3}+q+(3uv+p)(u+v)=0}
u
3
+
v
3
+
q
=
0
{\displaystyle u^{3}+v^{3}+q=0\;}
3
u
v
+
p
=
0
{\displaystyle \;3uv+p=0}
u
,
v
{\displaystyle u,v}
y
{\displaystyle y}
u
3
+
v
3
=
−
q
,
u
v
=
−
p
3
{\displaystyle u^{3}+v^{3}=-q\;\;,\;\;uv=-{{p} \over {3}}}
u
3
v
3
=
(
u
v
)
3
=
(
−
p
3
)
3
{\displaystyle u^{3}v^{3}=(uv)^{3}=\left(-{{p} \over {3}}\right)^{3}}
이 식은
u
3
{\displaystyle u^{3}}
2차 방정식 이고 근과 계수의 관계 에서
이 두개의 식으로부터
v
{\displaystyle v}
(
u
3
)
2
+
q
(
u
3
)
−
(
p
3
)
3
=
0
{\displaystyle \left(u^{3}\right)^{2}+q\left(u^{3}\right)-\left({p \over 3}\right)^{3}=0}
u
6
+
q
u
3
−
(
p
3
)
3
=
0
{\displaystyle u^{6}+qu^{3}-\left({p \over 3}\right)^{3}=0}
근의 공식 으로부터
u
3
=
−
q
±
q
2
−
4
(
−
p
3
)
3
2
{\displaystyle u^{3}={{-{q}\pm {\sqrt {{q}^{2}-4\left(-{p \over 3}\right)^{3}}}} \over {2}}}
u
3
=
−
q
4
±
q
2
4
−
4
(
−
p
3
)
3
4
2
4
{\displaystyle u^{3}={{-{{q} \over {\sqrt {4}}}\pm {\sqrt {{q^{2} \over 4}-{{4\left(-{p \over 3}\right)^{3}} \over {4}}}}} \over {{2} \over {\sqrt {4}}}}}
u
3
=
−
q
2
±
q
2
4
−
(
−
p
3
)
3
{\displaystyle u^{3}=-{{q} \over {2}}\pm {\sqrt {{q^{2} \over 4}-\left(-{p \over 3}\right)^{3}}}}
이것은 근의 공식 에서
q
{\displaystyle q}
u
3
=
−
q
2
±
(
q
2
)
2
+
(
p
3
)
3
{\displaystyle u^{3}=-{q \over 2}\pm {\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}
u
{\displaystyle u}
v
{\displaystyle v}
u
3
{\displaystyle u^{3}}
v
3
{\displaystyle v^{3}}
각각의 세제곱근 의 합으로서
y
=
−
q
2
+
(
q
2
)
2
+
(
p
3
)
3
3
+
−
q
2
−
(
q
2
)
2
+
(
p
3
)
3
3
{\displaystyle y={\sqrt[{3}]{-{q \over 2}+{\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}}}
이 구해진다. 이 해법이 발견된 당시에는 아직 복소수 가 알려지지 않았기 때문에 이 방법으로 해를 찾아내었으나, 이후 복소수에 관한 연구가 진행되어 이항방정식 x 3 = a 의 해가 ω를 1 의 세제곱근으로서
a
3
,
ω
a
3
,
ω
2
a
3
{\displaystyle {\sqrt[{3}]{a}},\omega {\sqrt[{3}]{a}},\omega ^{2}{\sqrt[{3}]{a}}}
복소근 이 있는 것이 알려지게 되었고,
x
3
=
1
{\displaystyle x^{3}=1}
x
3
−
1
=
0
{\displaystyle x^{3}-1=0}
(
x
−
1
)
(
x
2
+
x
+
1
)
=
0
{\displaystyle \left(x-1\right)\left(x^{2}+x+1\right)=0}
(
x
−
1
)
=
0
{\displaystyle \left({x-1}\right)=0}
(
x
2
+
x
+
1
)
=
0
{\displaystyle \left(x^{2}+x+1\right)=0}
x
=
1
{\displaystyle x=1}
(
x
2
+
x
+
1
)
=
x
2
+
x
+
1
{\displaystyle \left(x^{2}+x+1\right)=x^{2}+x+1}
근의 공식 에 의해
x
=
−
1
±
−
3
2
=
−
1
±
3
i
2
{\displaystyle x={-1\pm {\sqrt {-3}} \over 2}={-1\pm {\sqrt {3}}i \over 2}}
ω
=
−
1
+
3
i
2
{\displaystyle \omega ={-1+{\sqrt {3}}i \over 2}}
ω
2
=
−
1
−
3
i
2
{\displaystyle \omega ^{2}={-1-{\sqrt {3}}i \over 2}}
ω
3
=
ω
2
∗
ω
=
(
−
1
−
3
i
2
)
(
−
1
+
3
i
2
)
=
1
{\displaystyle \omega ^{3}=\omega ^{2}*\omega =\left({-1-{\sqrt {3}}i \over 2}\right)\left({-1+{\sqrt {3}}i \over 2}\right)=1}
ω
2
+
ω
=
(
−
1
−
3
i
2
)
+
(
−
1
+
3
i
2
)
=
−
1
{\displaystyle \omega ^{2}+\omega =\left({-1-{\sqrt {3}}i \over 2}\right)+\left({-1+{\sqrt {3}}i \over 2}\right)=-1}
∴
ω
3
+
ω
2
+
ω
=
0
{\displaystyle \therefore \omega ^{3}+\omega ^{2}+\omega =0}
u 의 세제곱근을 취할 때에도 마찬가지로 3개의 경우를 생각하게 되어서 각각 대응하는 v 를 요구하는 것으로
y
=
ω
k
−
q
2
+
(
q
2
)
2
+
(
p
3
)
3
3
+
ω
3
−
k
−
q
2
−
(
q
2
)
2
+
(
p
3
)
3
3
,
(
k
=
0
,
1
,
2
)
{\displaystyle y=\omega ^{k}{\sqrt[{3}]{-{q \over 2}+{\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}}+\omega ^{3-k}{\sqrt[{3}]{-{q \over 2}-{\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}},(k=0,1,2)}
해로서 알려지게 되었다.
또한,
x
3
+
y
3
+
z
3
−
3
x
y
z
{\displaystyle x^{3}+y^{3}+z^{3}-3xyz}
=
(
x
+
y
+
z
)
(
x
2
+
y
2
+
z
2
−
x
y
−
y
z
−
z
x
)
{\displaystyle =(x+y+z)(x^{2}+y^{2}+z^{2}-xy-yz-zx)}
=
(
x
+
y
+
z
)
(
x
2
−
(
y
+
z
)
x
+
y
2
−
y
z
+
z
2
)
{\displaystyle =(x+y+z)(x^{2}-(y+z)x+y^{2}-yz+z^{2})}
식의 인수분해로도 카르다노의 방법을 설명 할 수 있다.
y
3
+
z
3
=
q
{\displaystyle y^{3}+z^{3}=q}
−
3
y
z
=
p
{\displaystyle -3yz=p}
위 식은 p , q 로부터 y , z 을 요구하는 것으로
x
3
+
p
x
+
q
=
0
{\displaystyle x^{3}+px+q=0}
(
x
+
y
+
z
)
(
x
2
+
y
2
+
z
2
−
x
y
−
y
z
−
z
x
)
=
0
{\displaystyle (x+y+z)(x^{2}+y^{2}+z^{2}-xy-yz-zx)=0}
(
x
+
y
+
z
)
(
x
2
−
(
y
+
z
)
x
+
y
2
−
y
z
+
z
2
)
=
0
{\displaystyle (x+y+z)(x^{2}-(y+z)x+y^{2}-yz+z^{2})=0}
이렇게 되는 3차 방정식을 인수분해로 계산해낼 수 있다. 이 방법은 카르다노의 방법과 같다.
카르다노의 공식에서
x
3
+
p
x
+
q
=
0
{\displaystyle x^{3}+px+q=0}
이런 최고차항이 사라진 3차 방정식은
x
=
u
+
v
{\displaystyle x=u+v}
(
q
2
)
2
+
(
p
3
)
3
<
0
{\displaystyle \left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}<0}
이 때의 음수의 제곱근이 나타난다. 이것은 이 방정식의 판별식
D
=
4
p
3
+
27
q
2
{\displaystyle D=4p^{3}+27q^{2}}
과 같은 조건이다.
즉
D
<
0
{\displaystyle D<0}
라파엘 봄벨리 (Rafael Bombelli )는 이 경우를 자세하게 연구해 1572년에 출판한 「대수학」(Algebra)에 적었다. 형식적인 계산이긴 하지만 당시에는 아직 알려지지 않았다 이 계산은 허수의 계산과 같았다. 본베리는
x
3
=
15
x
+
4
{\displaystyle x^{3}=15x+4}
이런 공식에 x = 4를 해로 가지는 방정식에 예를 주었다 이 방정식을 카르다노의 공식에서 계산해 보면
x
=
u
+
v
{\displaystyle x=u+v}
u
3
+
v
3
=
(
2
+
−
121
)
+
(
2
−
−
121
)
{\displaystyle u^{3}+v^{3}=\left({2+{\sqrt {-121}}}\right)+\left({2-{\sqrt {-121}}}\right)}
u
+
v
=
2
+
−
121
3
+
2
−
−
121
3
{\displaystyle u+v={\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}}
이 되지만 본베리는 이 우변은 오늘날의 공역의 복소수화 라고 생각해 음수의 제곱근 연산 규칙을 준 다음
(
2
±
b
−
1
)
3
=
2
±
−
121
{\displaystyle \left(2\pm b{\sqrt {-1}}\right)^{3}=2\pm {\sqrt {-121}}}
로부터 b = 1 을 요구하여 원 방정식이 x = 4를 해로 가지는 것을 설명했다.
일반적으로는
(
a
±
b
−
1
)
3
=
2
±
−
121
{\displaystyle \left(a\pm b{\sqrt {-1}}\right)^{3}=2\pm {\sqrt {-121}}}
로부터 a , b 의 두개의 값을 요구하지 않으면 안되지만 이것을 요구하기 위해서는 다른 3차방정식이 나타나기 때문에 카르다노는 이 경우를 환원불능 (casus irreducibilis)이라고 불렀다. 이 환원 불능의 경우를 회피하기 위해서 여러 가지 노력이 이루어졌지만 실은 허수를 피해서 실수의 거듭제곱근과 사칙연산을 유한하게 사용하는 것으로는 해를 찾아내는 것은 불가능 하기 때문에 모두 헛수고로 끝났다.
이후에 허수단위
i
{\displaystyle i}
x
3
=
15
x
+
4
{\displaystyle x^{3}=15x+4}
x
3
−
15
x
−
4
=
0
{\displaystyle x^{3}-15x-4=0}
x
3
+
p
x
+
q
=
0
{\displaystyle x^{3}+px+q=0}
x
=
u
+
v
{\displaystyle x=u+v}
u
6
+
q
u
3
+
p
=
0
{\displaystyle u^{6}+qu^{3}+p=0}
u
3
=
−
q
2
±
(
q
2
)
2
+
(
p
3
)
3
{\displaystyle u^{3}=-{q \over 2}\pm {\sqrt {\left({q \over 2}\right)^{2}+\left({p \over 3}\right)^{3}}}}
−
(
−
4
)
2
±
(
(
−
4
)
2
)
2
+
(
(
−
15
)
3
)
3
{\displaystyle -{(-4) \over 2}\pm {\sqrt {\left({(-4) \over 2}\right)^{2}+\left({(-15) \over 3}\right)^{3}}}}
2
±
(
4
)
+
(
−
125
)
{\displaystyle 2\pm {\sqrt {(4)+(-125)}}}
2
±
−
121
{\displaystyle 2\pm {\sqrt {-121}}}
u
3
=
2
±
−
121
{\displaystyle u^{3}=2\pm {\sqrt {-121}}}
이 세제곱근이 곱해서
−
p
3
{\displaystyle -{p \over 3}}
u
,
v
{\displaystyle u,v}
3
u
v
+
p
=
0
{\displaystyle 3uv+p=0}
u
v
=
−
p
3
{\displaystyle uv=-{{p} \over {3}}}
이 세제곱근이 곱해서
−
(
−
15
)
3
{\displaystyle -{(-15) \over 3}}
2
+
−
121
3
{\displaystyle {\sqrt[{3}]{2+{\sqrt {-121}}}}}
−
2
−
−
121
3
{\displaystyle -{\sqrt[{3}]{2-{\sqrt {-121}}}}}
x
=
u
+
v
{\displaystyle x=u+v}
u
3
+
v
3
=
−
q
{\displaystyle u^{3}+v^{3}=-q}
1에대한 3차방정식의 복소근을 사용해서 허수
i
{\displaystyle i}
복소근
ω
{\displaystyle \omega }
ω
2
{\displaystyle \omega ^{2}}
ω
3
{\displaystyle \omega ^{3}}
2
+
−
121
3
+
2
−
−
121
3
,
{\displaystyle {\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}\;\;,}
2
+
−
121
3
ω
+
2
−
−
121
3
ω
2
,
{\displaystyle {\sqrt[{3}]{2+{\sqrt {-121}}}}\;\omega +{\sqrt[{3}]{2-{\sqrt {-121}}}}\;\omega ^{2}\;\;,}
2
+
−
121
3
ω
2
+
2
−
−
121
3
ω
{\displaystyle {\sqrt[{3}]{2+{\sqrt {-121}}}}\;\omega ^{2}+{\sqrt[{3}]{2-{\sqrt {-121}}}}\;\omega }
이다.