감마 분포

감마 분포는 연속 확률분포로, 두 개의 매개변수를 받으며 양의 실수를 가질 수 있다.

감마 분포

확률 밀도 함수
누적 분포 함수
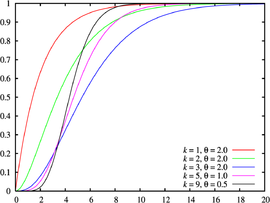
매개변수	$k>0\,$ 형상모수 $\theta >0\,$ 척도모수
지지집합	$x\in (0;\infty )\!$
확률 밀도	$x^{k-1}{\frac {\exp \left(-x/\theta \right)}{\Gamma (k)\,\theta ^{k}}}$
누적 분포	${\frac {\gamma (k,x/\theta )}{\Gamma (k)}}$
기댓값	$k\theta \,$
최빈값	$(k-1)\theta \,$ for $k\geq 1\,$
분산	$k\theta ^{2}\,$
비대칭도	${\frac {2}{\sqrt {k}}}$
첨도	${\frac {3(k+2)}{k}}$
엔트로피	$k\theta +(1-k)\ln(\theta )+\ln(\Gamma (k))\,$ $+(1-k)\psi (k)\,$
적률생성함수	$(1-\theta \,t)^{-k}{\mbox{ for }}t<{\frac {1}{\theta }}$
특성함수	$(1-\theta \,i\,t)^{-k}$

감마 분포는 지수 분포나 푸아송 분포 등의 매개변수에 대한 켤레 사전 확률 분포이며, 이에 따라 베이즈 확률론에서 사전 확률 분포로 사용된다.

매개변수 $k$가 정수인 경우 감마 분포는 얼랑 분포가 된다.

확률 밀도 함수

감마 분포의 확률 밀도 함수는 감마 함수를 써서 나타낼 수 있다.

$f(x;k,\theta )=x^{k-1}{\frac {e^{-x/\theta }}{\theta ^{k}\,\Gamma (k)}}\ \mathrm {for} \ x>0\,\!$

여기서 $k(>0)$는 형상모수이고, $\theta (>0)$는 척도모수이다.

성질

만약 확률변수 $X_{1},\cdots ,X_{n}$가 독립이며 각각 $X_{i}\sim \mathrm {Gamma} (k_{i},\theta )$의 분포를 가진다면, 확률변수들의 합은 다음과 같은 분포를 따른다.

$\sum _{i}X_{i}\sim \mathrm {Gamma} (\sum _{i}k_{i},\theta )$

$X\sim \mathrm {Gamma} (k,\theta )$인 확률변수 $X$에 상수를 곱한 경우는 척도모수에 영향을 준다.

$cX\sim \mathrm {Gamma} (k,c\theta )$

다른 분포와의 관계

• 모양 매개변수 $k$가 정수인 경우 얼랑 분포에 포함된다.
• $k=1,\theta =1/\lambda$는 지수 분포가 된다.
• $k=\nu /2,\theta =2$는 카이제곱 분포가 된다. 이 때 자유도는 $\nu$이다.

켤레 사전 확률

감마 분포는 푸아송 분포, 지수 분포, 정규 분포(평균을 알고 있을 경우), 파레토 분포, 감마 분포(모양 매개변수를 알 경우)와 역감마 분포(모양 매개변수를 알 경우) 등의 분포와 켤레 사전 확률 분포를 이룬다.

같이 보기

• 확률분포
  • 지수분포
  • 얼랑 분포(Erlang distribution)
  • 일반화 감마 분포(Generalized gamma distribution)
  • 카이제곱 분포