삼각행렬

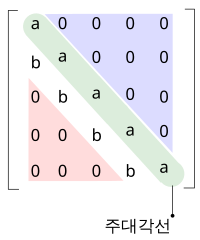
선형대수학에서 삼각행렬(三角行列, 영어: triangular matrix)은 정사각행렬의 특수한 경우로, 주대각선을 기준으로 대각항의 위쪽이나 아래쪽 항들의 값이 모두 0인 경우를 의미한다.

주대각선

다음과 같은 모양을 가지는 행렬 $\mathbf {L}$을 하삼각행렬(lower triangular matrix)로 정의한다.

$\mathbf {L} ={\begin{bmatrix}l_{1,1}&&&&0\\l_{2,1}&l_{2,2}&&&\\l_{3,1}&l_{3,2}&\ddots &&\\\vdots &\vdots &\ddots &\ddots &\\l_{n,1}&l_{n,2}&\ldots &l_{n,n-1}&l_{n,n}\end{bmatrix}}$

다음과 같은 모양을 가지는 행렬 $\mathbf {U}$을 상삼각행렬(upper triangular matrix)로 정의한다.

$\mathbf {U} ={\begin{bmatrix}u_{1,1}&u_{1,2}&u_{1,3}&\ldots &u_{1,n}\\&u_{2,2}&u_{2,3}&\ldots &u_{2,n}\\&&\ddots &\ddots &\vdots \\&&&\ddots &u_{n-1,n}\\0&&&&u_{n,n}\end{bmatrix}}$

만약 삼각행렬의 대각항이 모두 0인 경우는 순삼각행렬(strict triangular), 혹은 삼각행렬의 모양에 따라 순하삼각행렬, 순상삼각행렬로 부른다.

성질

• 상삼각행렬이면서 하삼각행렬인 행렬은 대각행렬이다.
• 삼각행렬이면서 정규행렬인 행렬은 대각행렬이다.
• 상삼각행렬은 덧셈, 곱셈, 역행렬에 대해 닫혀 있다. 즉, 상삼각행렬간의 덧셈, 곱셈, 역행렬 연산을 통해 나오는 행렬은 상삼각행렬이다. 이 성질은 하삼각행렬에 대해서도 성립한다.
  • 단, 순삼각행렬 등과 같이 행렬식이 0의 값을 가질 경우 역행렬이 존재하지 않으므로, 역행렬에 대해 닫혀있기 위해서는 삼각행렬이 가역행렬이어야 한다는 추가 조건이 있다.
• 삼각행렬의 행렬식은 대각항들의 곱과 같다.
• 대각행렬과 사다리꼴행렬은 삼각행렬의 특수한 형태이다.

예

• (순)상삼각행렬(식)

$+eee{\begin{vmatrix}{\color {red}{4a}}&3b&2c&d\\0&{\color {red}{4a}}&3b&2c\\0&0&{\color {red}{4a}}&3b\\0&0&0&{\color {red}{4a}}\\\end{vmatrix}}=+eee\left({\color {red}{4a}}{\begin{vmatrix}{\color {red}{4a}}&3b&2c\\0&{\color {red}{4a}}&3b\\0&0&{\color {red}{4a}}\\\end{vmatrix}}-3b{\begin{vmatrix}0&3b&2c\\0&4a&3b\\0&0&4a\\\end{vmatrix}}+2c{\begin{vmatrix}0&4a&2c\\0&0&3b\\0&0&4a\\\end{vmatrix}}-d{\begin{vmatrix}0&4a&3b\\0&0&4a\\0&0&0\\\end{vmatrix}}\right)$

$+eee{\color {red}{4a}}{\begin{vmatrix}{\color {red}{4a}}&3b&2c\\0&{\color {red}{4a}}&3b\\0&0&{\color {red}{4a}}\\\end{vmatrix}}=+eee{\color {red}{4a}}\left({\color {red}{4a}}{\begin{vmatrix}{\color {red}{4a}}&3b\\0&{\color {red}{4a}}\\\end{vmatrix}}-3b{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}+2c{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}\right)$

$-eee3b{\begin{vmatrix}0&3b&2c\\0&4a&3b\\0&0&4a\\\end{vmatrix}}=-eee3b\left({\cancel {0{\begin{vmatrix}4a&3b\\0&4a\\\end{vmatrix}}}}-3b{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}+2c{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}\right)$

$+eee2c{\begin{vmatrix}0&4a&2c\\0&0&3b\\0&0&4a\\\end{vmatrix}}=+eee2c\left({\cancel {0{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}}}-4a{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}+2c{\begin{vmatrix}0&0\\0&0\\\end{vmatrix}}\right)$

$-eeed{\begin{vmatrix}0&4a&3b\\0&0&4a\\0&0&0\\\end{vmatrix}}=-eeed\left({\cancel {0{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}}}-4a{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}+3b{\begin{vmatrix}0&0\\0&0\\\end{vmatrix}}\right)$

$+eee{\color {red}{4a4a}}{\begin{vmatrix}{\color {red}{4a}}&3b\\0&{\color {red}{4a}}\\\end{vmatrix}}=+eee{\color {red}{4a4a}}({\color {red}{4a4a}}-{\cancel {3b0}})=+{\color {red}{4^{4}a^{4}}}e^{3}=+{\color {red}{256a^{4}}}e^{3}$

$-eee4a3b{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}=-eee4a3b(04a-3b0)=0$

$+eee4a2c{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}=+eee4a2c(00-4a0)=0$

$+eee3b3b{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}=+eee3b3b(04a-3b0)=0$

$-eee3b2c{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}=-eee3b2c(00-4a0)=0$

$-eee2c4a{\begin{vmatrix}0&3b\\0&4a\\\end{vmatrix}}=-eee2c4a(04a-3b0)=0$

$+eee2c2c{\begin{vmatrix}0&0\\0&0\\\end{vmatrix}}=+eee2c2c(00-00)=0$

$+eeed4a{\begin{vmatrix}0&4a\\0&0\\\end{vmatrix}}=+eeed4a(00-4a0)=0$

$-eeed3b{\begin{vmatrix}0&0\\0&0\\\end{vmatrix}}=-eeed3b(00-00)=0$

• (순)하삼각행렬(식)

$aaa{\begin{vmatrix}{\color {red}{d}}&0&0&0\\2c&{\color {red}{d}}&0&0\\3b&2c&{\color {red}{d}}&0\\4a&3b&2c&{\color {red}{d}}\\\end{vmatrix}}=aaa\left({\color {red}{d}}{\begin{vmatrix}{\color {red}{d}}&0&0\\2c&{\color {red}{d}}&0\\3b&2c&{\color {red}{d}}\\\end{vmatrix}}-{\cancel {0{\begin{vmatrix}2c&0&0\\3b&d&0\\4a&2c&d\\\end{vmatrix}}+0{\begin{vmatrix}2c&d&0\\3b&2c&0\\4a&3b&d\\\end{vmatrix}}-0{\begin{vmatrix}2c&d&0\\3b&2c&d\\4a&3b&2c\\\end{vmatrix}}}}\right)$

$aaa{\color {red}{d}}{\begin{vmatrix}{\color {red}{d}}&0&0\\2c&{\color {red}{d}}&0\\3b&2c&{\color {red}{d}}\\\end{vmatrix}}=aaa{\color {red}{d}}\left({\color {red}{d}}{\begin{vmatrix}{\color {red}{d}}&0\\2c&{\color {red}{d}}\\\end{vmatrix}}{\cancel {-0{\begin{vmatrix}2c&0\\3b&d\\\end{vmatrix}}+0{\begin{vmatrix}2c&d\\3b&2c\\\end{vmatrix}}}}\right)$

$aaa{\color {red}{dd}}{\begin{vmatrix}{\color {red}{d}}&0\\2c&{\color {red}{d}}\\\end{vmatrix}}=aaa{\color {red}{dd}}({\color {red}{dd}}-{\cancel {02c}})=a^{3}{\color {red}{d^{4}}}$

• 삼각행렬 $A$에 대해서 $xI-A$도 역시 삼각행렬이기 때문에, 고유행렬식 $det(xI-A)$은 대각항들을 근으로 가진다. 따라서 $A$의 고윳값은 각 대각항이 된다.

• 단위 하삼각행렬

${\begin{bmatrix}1&0&0&0\\\blacksquare &1&0&0\\\blacksquare &\blacksquare &1&0\\\blacksquare &\blacksquare &\blacksquare &1\\\end{bmatrix}}$

전진 대입과 후진 대입

행렬 방정식 $\mathbf {L} \mathbf {x} =\mathbf {b}$ 또는 $\mathbf {U} \mathbf {x} =\mathbf {b}$의 형태에서 각각 하삼각행렬에 대한 전진대입( forward substitution) 및 상 삼각행렬에대한 후진대입(back substitution)이라고하는 반복적 프로세스로 해결하기가 용이하다. 우선 소위 하삼각행렬의 경우의 프로세스는 $x_{1}$을 첫번째 계산으로 해서 다음 방정식으로 대입하여 $x_{2}$ , ~$x_{n}$까지 반복한다. 상삼각행렬에서는 역으로 작동하는데 , 첫번째 계산은 $x_{n}$, 그런 다음 이를 이전 방정식으로 대입하여 $x_{n-1}$, 반복하여 $x_{1}$에 이른다.

행렬을 뒤집는것은 아니다.

• 전진대입

행렬 방정식 L x = b는 선형 방정식의 시스템(연립)으로 쓸 수 있다

${\begin{matrix}\ell _{1,1}x_{1}&&&&&=&b_{1}\\\ell _{2,1}x_{1}&+&\ell _{2,2}x_{2}&&&=&b_{2}\\\vdots &&\vdots &\ddots &&&\vdots \\\ell _{(m-1),1}x_{1}&+&\ell _{(m-1),2}x_{2}&+\dotsb +&\ell _{(m-1),(m-1)}x_{(m-1)}&=&b_{(m-1)}\\\ell _{m,1}x_{1}&+&\ell _{m,2}x_{2}&+\dotsb +&\ell _{m,m}x_{m}&=&b_{m}\\\end{matrix}}$

여기서 $x_{1}$는 첫 번째 방정식 ($\ell _{1,1}x_{1}=b_{1}$) 에만 관련된다. 이어서 두 번째 방정식은 $x_{1}$ 과 $x_{2}$에 관련된다. 따라서 이미 해결 된 값으로 대입하여 풀수있게된다. 계속해서 마지막의 직전은 $x_{m}$이전에 접근한 값 $x_{m-1}$이다. 그리고 맨 마지막 $m$번째 방정식은 $x_{m}$이다.

이러한 $x_{1},x_{2},\dots ,x_{m-1},x_{m}$ 결과 수식은 다음과 같다.

$x_{1}{\ell _{1,1}}={b_{1}}$

$x_{1}={\frac {b_{1}}{\ell _{1,1}}}$ 이고,

$x_{2}{\ell _{2,2}}+\ell _{2,1}x_{1}=b_{2}$

$x_{2}={\frac {b_{2}-\ell _{2,1}x_{1}}{\ell _{2,2}}}$ 이고,

$x_{3}{\ell _{3,3}}+x_{2}{\ell _{2,2}}+\ell _{2,1}x_{1}=b_{3}$

$x_{3}={{b_{3}-x_{2}{\ell _{2,2}}-\ell _{2,1}x_{1}} \over {\ell _{3,3}}}$ 이고,

정리하면,

$x_{1}={\frac {b_{1}}{\ell _{1,1}}}$

$x_{2}={\frac {b_{2}-\ell _{2,1}x_{1}}{\ell _{2,2}}}$

$x_{3}={{b_{3}-x_{2}{\ell _{2,2}}-\ell _{2,1}x_{1}} \over {\ell _{3,3}}}$

계속해서 ,

$\vdots$

일반화하면

$x_{m}={{b_{m}-\left(\sum _{i=1}^{m-1}\ell _{m,i}x_{i}\right)} \over {\ell _{m,m}}}$

• 후진대입

상삼각행렬 U를 갖는 행렬 방정식은 역방향에서 같은 방식으로 적용하여 접근할 수 있다.

같이 보기

• 사다리꼴행렬
• LU 분해

참고 문헌

• 매스월드
• Abdelwahab Kharab; Ronald B. Guenther (2013). 《An Introduction to Numerical Methods A MATLAB Approach》 [이공학도를 위한 수치해석]. 학산미디어. ISBN 978-89-966211-8-8. 
• 매스월드
• 매스월드
• 정보통신기술용어해설