환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
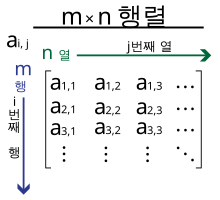
행렬 은 각 행
i
∈
{
1
,
…
,
m
}
{\displaystyle i\in \{1,\dotsc ,m\}}
j
∈
{
1
,
…
,
n
}
{\displaystyle j\in \{1,\dotsc ,n\}}
순서쌍
(
i
,
j
)
{\displaystyle (i,j)}
A
i
j
∈
R
{\displaystyle A_{ij}\in R}
함수
A
=
(
A
i
j
)
i
,
j
{\displaystyle A=(A_{ij})_{i,j}}
[ 2] :98
행렬
A
{\displaystyle A}
소괄호 또는 대괄호 를 추가하여
(
A
11
A
12
A
13
⋯
A
1
n
A
21
A
22
A
23
⋯
A
2
n
A
31
A
32
A
33
⋯
A
3
n
⋮
⋮
⋮
⋱
⋮
A
m
1
A
m
2
A
m
3
⋯
A
m
n
)
{\displaystyle {\begin{pmatrix}A_{11}&A_{12}&A_{13}&\cdots &A_{1n}\\A_{21}&A_{22}&A_{23}&\cdots &A_{2n}\\A_{31}&A_{32}&A_{33}&\cdots &A_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\A_{m1}&A_{m2}&A_{m3}&\cdots &A_{mn}\end{pmatrix}}}
또는
[
A
11
A
12
A
13
⋯
A
1
n
A
21
A
22
A
23
⋯
A
2
n
A
31
A
32
A
33
⋯
A
3
n
⋮
⋮
⋮
⋱
⋮
A
m
1
A
m
2
A
m
3
⋯
A
m
n
]
{\displaystyle {\begin{bmatrix}A_{11}&A_{12}&A_{13}&\cdots &A_{1n}\\A_{21}&A_{22}&A_{23}&\cdots &A_{2n}\\A_{31}&A_{32}&A_{33}&\cdots &A_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\A_{m1}&A_{m2}&A_{m3}&\cdots &A_{mn}\end{bmatrix}}}
와 같이 표기한다.
각
A
i
j
{\displaystyle A_{ij}}
A
{\displaystyle A}
i
{\displaystyle i}
j
{\displaystyle j}
성분 (成分, 영어 : entry ) 또는 원소 (元素, 영어 : element ) 또는 계수 (係數, 영어 : coefficient )라고 한다. 행렬
A
{\displaystyle A}
A
i
j
{\displaystyle A_{ij}}
A
i
,
j
{\displaystyle A_{i,j}}
a
i
j
{\displaystyle a_{ij}}
a
i
,
j
{\displaystyle a_{i,j}}
A
(
i
,
j
)
{\displaystyle A(i,j)}
A
[
i
,
j
]
{\displaystyle A[i,j]}
A
i
i
{\displaystyle A_{ii}}
i
∈
{
1
,
…
,
min
{
m
,
n
}
}
{\displaystyle i\in \{1,\dotsc ,\min\{m,n\}\}}
A
{\displaystyle A}
대각 성분 (對角成分, 영어 : diagonal entry ) 또는 대각 원소 (對角元素, 영어 : diagonal element ) 또는 대각 요소 (對角要素) 또는 주대각선 [ 2] :99
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
Mat
(
m
,
n
;
R
)
{\displaystyle \operatorname {Mat} (m,n;R)}
M
m
,
n
(
R
)
{\displaystyle \operatorname {M} _{m,n}(R)}
행렬
A
{\displaystyle A}
크기 (영어 : size )는 행과 열의 수의 순서쌍
(
m
,
n
)
{\displaystyle (m,n)}
m
×
n
{\displaystyle m\times n}
만약 행과 열의 수가 같다면 (
m
=
n
{\displaystyle m=n}
A
{\displaystyle A}
정사각 행렬 (正四角行列, 영어 : square matrix ) 또는 정방 행렬 (正方行列)이라고 한다. 환
R
{\displaystyle R}
n
×
n
{\displaystyle n\times n}
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
M
n
(
R
)
{\displaystyle \operatorname {M} _{n}(R)}
만약
m
=
1
{\displaystyle m=1}
A
{\displaystyle A}
1
×
n
{\displaystyle 1\times n}
행벡터 (行-, 영어 : row vector )라고 한다.
만약
n
=
1
{\displaystyle n=1}
A
{\displaystyle A}
m
×
1
{\displaystyle m\times 1}
열벡터 (列-, 영어 : column vector )라고 한다. 특히, 행렬
A
{\displaystyle A}
i
{\displaystyle i}
j
{\displaystyle j}
A
i
,
−
=
(
A
i
1
A
i
2
⋯
A
i
n
)
{\displaystyle A_{i,-}={\begin{pmatrix}A_{i1}&A_{i2}&\cdots A_{in}\end{pmatrix}}}
와
A
−
,
j
(
A
1
j
A
2
j
⋮
A
m
j
)
{\displaystyle A_{-,j}{\begin{pmatrix}A_{1j}\\A_{2j}\\\vdots \\A_{mj}\end{pmatrix}}}
이며, 이를 통해 행렬을 다음과 같이 나타낼 수 있다.
A
=
(
A
1
,
−
A
2
,
−
⋮
A
m
,
−
)
=
(
A
−
,
1
A
−
,
2
⋯
A
−
,
n
)
{\displaystyle A={\begin{pmatrix}A_{1,-}\\A_{2,-}\\\vdots \\A_{m,-}\end{pmatrix}}={\begin{pmatrix}A_{-,1}&A_{-,2}&\cdots &A_{-,n}\end{pmatrix}}}
행렬들에 대하여 덧셈, 스칼라배, 곱셈, 전치 행렬 등의 연산을 정의할 수 있으며, 정사각 행렬은 역행렬 , 대각합 , 행렬식 등 연산이 추가로 정의된다. 덧셈은 같은 크기의 두 행렬에 대해서만 정의되며, 곱셈은 오직 첫 번째 행렬의 열의 수와 두 번째 행렬의 행의 수가 같은 경우에만 정의된다.[ 2] :99 역행렬 은 가역 정사각 행렬에 대하여 정의되며, 행렬식 은 가환환 위의 정사각 행렬에 대하여 정의된다.
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
,
B
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A,B\in \operatorname {Mat} (m,n;R)}
A
+
B
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A+B\in \operatorname {Mat} (m,n;R)}
m
×
n
{\displaystyle m\times n}
i
{\displaystyle i}
j
{\displaystyle j}
(
A
+
B
)
i
j
=
A
i
j
+
B
i
j
{\displaystyle (A+B)_{ij}=A_{ij}+B_{ij}}
이다.
실수 행렬의 예는 다음과 같다.
(
1
3
7
1
0
0
)
+
(
0
0
5
7
5
0
)
=
(
1
+
0
3
+
0
7
+
5
1
+
7
0
+
5
0
+
0
)
=
(
1
3
12
8
5
0
)
{\displaystyle {\begin{pmatrix}1&3&7\\1&0&0\end{pmatrix}}+{\begin{pmatrix}0&0&5\\7&5&0\end{pmatrix}}={\begin{pmatrix}1+0&3+0&7+5\\1+7&0+5&0+0\end{pmatrix}}={\begin{pmatrix}1&3&12\\8&5&0\end{pmatrix}}}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
r
∈
R
{\displaystyle r\in R}
r
A
,
A
r
∈
Mat
(
m
,
n
;
R
)
{\displaystyle rA,Ar\in \operatorname {Mat} (m,n;R)}
m
×
n
{\displaystyle m\times n}
(
r
A
)
i
j
=
r
A
i
j
{\displaystyle (rA)_{ij}=rA_{ij}}
(
A
r
)
i
j
=
A
i
j
r
{\displaystyle (Ar)_{ij}=A_{ij}r}
만약
R
{\displaystyle R}
가환환 일 경우, 이 두 연산은 일치하며, 이를 스칼라배라고 부른다.
실수 행렬의 예는 다음과 같다.
2
(
1
8
−
3
4
−
2
5
)
=
(
2
⋅
1
2
⋅
8
2
⋅
−
3
2
⋅
4
2
⋅
−
2
2
⋅
5
)
=
(
2
16
−
6
8
−
4
10
)
{\displaystyle 2{\begin{pmatrix}1&8&-3\\4&-2&5\end{pmatrix}}={\begin{pmatrix}2\cdot 1&2\cdot 8&2\cdot -3\\2\cdot 4&2\cdot -2&2\cdot 5\end{pmatrix}}={\begin{pmatrix}2&16&-6\\8&-4&10\end{pmatrix}}}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
Mat
(
m
,
n
;
R
)
{\displaystyle \operatorname {Mat} (m,n;R)}
(
R
,
R
)
{\displaystyle (R,R)}
쌍가군 을 이룬다. 만약
R
{\displaystyle R}
가환환 일 경우, 이는 (덧셈과 스칼라배에 따른)
R
{\displaystyle R}
가군 이 되며, 특히 만약
R
{\displaystyle R}
체 일 경우
R
{\displaystyle R}
벡터 공간 이다. 이 쌍가군 의 덧셈 항등원 은 영행렬
0
m
×
n
=
(
0
0
⋯
0
0
0
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
0
)
∈
Mat
(
m
,
n
;
R
)
{\displaystyle 0_{m\times n}={\begin{pmatrix}0&0&\cdots &0\\0&0&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &0\end{pmatrix}}\in \operatorname {Mat} (m,n;R)}
이며, 각 행렬
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
역원 은 성분별 덧셈 역원
−
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle -A\in \operatorname {Mat} (m,n;R)}
(
−
A
)
i
j
=
−
A
i
j
{\displaystyle (-A)_{ij}=-A_{ij}}
이다.
특히, 두 행렬
A
,
B
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A,B\in \operatorname {Mat} (m,n;R)}
A
−
B
=
A
+
(
−
B
)
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A-B=A+(-B)\in \operatorname {Mat} (m,n;R)}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
(
R
,
R
)
{\displaystyle (R,R)}
쌍가군
A
,
B
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A,B\in \operatorname {Mat} (m,n;R)}
m
n
{\displaystyle mn}
자유 가군 을 이루며, 오른쪽 가군으로서
m
n
{\displaystyle mn}
자유 가군 을 이룬다.
R
{\displaystyle R}
가환환 일 경우
m
n
{\displaystyle mn}
R
{\displaystyle R}
기저 는 다음과 같다.
E
i
j
∈
Mat
(
m
,
n
;
R
)
{\displaystyle E_{ij}\in \operatorname {Mat} (m,n;R)}
(
E
i
j
)
k
l
=
δ
i
k
δ
j
l
=
{
1
i
=
k
∧
j
=
l
0
i
≠
k
∨
j
≠
l
{\displaystyle (E_{ij})_{kl}=\delta _{ik}\delta _{jl}={\begin{cases}1&i=k\land j=l\\0&i\neq k\lor j\neq l\end{cases}}}
i
∈
{
1
,
…
,
m
}
{\displaystyle i\in \{1,\dotsc ,m\}}
j
∈
{
1
,
…
,
n
}
{\displaystyle j\in \{1,\dotsc ,n\}}
행렬 곱셈 환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
n
×
p
{\displaystyle n\times p}
B
∈
Mat
(
n
,
p
;
R
)
{\displaystyle B\in \operatorname {Mat} (n,p;R)}
A
B
∈
Mat
(
m
,
p
;
R
)
{\displaystyle AB\in \operatorname {Mat} (m,p;R)}
m
×
p
{\displaystyle m\times p}
i
{\displaystyle i}
j
{\displaystyle j}
A
{\displaystyle A}
i
{\displaystyle i}
B
{\displaystyle B}
j
{\displaystyle j}
스칼라곱 ’이다 (둘 모두
n
{\displaystyle n}
(
A
B
)
i
j
=
∑
k
=
1
n
A
i
k
B
k
j
=
A
i
1
B
1
j
+
A
i
2
B
2
j
+
⋯
A
i
n
B
n
j
{\displaystyle (AB)_{ij}=\sum _{k=1}^{n}A_{ik}B_{kj}=A_{i1}B_{1j}+A_{i2}B_{2j}+\cdots A_{in}B_{nj}}
다음은 실수 행렬의 예다.
(
1
0
2
−
1
3
1
)
(
3
1
2
1
1
0
)
=
(
1
⋅
3
+
0
⋅
2
+
2
⋅
1
1
⋅
1
+
0
⋅
1
+
2
⋅
0
−
1
⋅
3
+
3
⋅
2
+
1
⋅
1
−
1
⋅
1
+
3
⋅
1
+
1
⋅
0
)
=
(
5
1
4
2
)
{\displaystyle {\begin{pmatrix}1&0&2\\-1&3&1\\\end{pmatrix}}{\begin{pmatrix}3&1\\2&1\\1&0\end{pmatrix}}={\begin{pmatrix}1\cdot 3+0\cdot 2+2\cdot 1&1\cdot 1+0\cdot 1+2\cdot 0\\-1\cdot 3+3\cdot 2+1\cdot 1&-1\cdot 1+3\cdot 1+1\cdot 0\end{pmatrix}}={\begin{pmatrix}5&1\\4&2\end{pmatrix}}}
행벡터와 열벡터
A
=
(
A
1
,
−
A
2
,
−
⋮
A
m
,
−
)
{\displaystyle A={\begin{pmatrix}A_{1,-}\\A_{2,-}\\\vdots \\A_{m,-}\end{pmatrix}}}
B
=
(
B
−
,
1
B
−
,
2
⋯
B
−
,
n
)
{\displaystyle B={\begin{pmatrix}B_{-,1}&B_{-,2}&\cdots &B_{-,n}\end{pmatrix}}}
를 통해 행렬 곱셈을 다음과 같이 나타낼 수 있다.
A
B
=
(
A
1
,
−
B
A
2
,
−
B
⋮
A
m
,
−
B
)
=
(
A
B
−
,
1
A
B
−
,
2
⋯
A
B
−
,
n
)
=
(
A
1
,
−
B
−
,
1
A
1
,
−
B
−
,
2
⋯
A
1
,
−
B
−
,
p
A
2
,
−
B
−
,
1
A
2
,
−
B
−
,
2
⋯
A
2
,
−
B
−
,
p
⋮
⋮
⋱
⋮
A
m
,
−
B
−
,
1
A
m
,
−
B
−
,
2
⋯
A
m
,
−
B
−
,
p
)
{\displaystyle AB={\begin{pmatrix}A_{1,-}B\\A_{2,-}B\\\vdots \\A_{m,-}B\end{pmatrix}}={\begin{pmatrix}AB_{-,1}&AB_{-,2}&\cdots &AB_{-,n}\end{pmatrix}}={\begin{pmatrix}A_{1,-}B_{-,1}&A_{1,-}B_{-,2}&\cdots &A_{1,-}B_{-,p}\\A_{2,-}B_{-,1}&A_{2,-}B_{-,2}&\cdots &A_{2,-}B_{-,p}\\\vdots &\vdots &\ddots &\vdots \\A_{m,-}B_{-,1}&A_{m,-}B_{-,2}&\cdots &A_{m,-}B_{-,p}\end{pmatrix}}}
행렬 곱셈은 결합 법칙 을 만족시킨다. 즉, 환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
n
×
p
{\displaystyle n\times p}
B
∈
Mat
(
n
,
p
;
R
)
{\displaystyle B\in \operatorname {Mat} (n,p;R)}
p
×
q
{\displaystyle p\times q}
C
∈
Mat
(
p
,
q
;
R
)
{\displaystyle C\in \operatorname {Mat} (p,q;R)}
(
A
B
)
C
=
A
(
B
C
)
{\displaystyle (AB)C=A(BC)}
가 성립한다.
행렬 곱셈은 함수
Mat
(
m
,
n
;
R
)
⊕
Mat
(
n
,
p
;
R
)
→
Mat
(
m
,
p
;
R
)
{\displaystyle \operatorname {Mat} (m,n;R)\oplus \operatorname {Mat} (n,p;R)\to \operatorname {Mat} (m,p;R)}
로서
(
R
,
R
)
{\displaystyle (R,R)}
특히, 환
R
{\displaystyle R}
(
R
,
R
)
{\displaystyle (R,R)}
쌍가군
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
R
{\displaystyle R}
결합 대수 를 이룬다. 특히 환 을 이루며, 행렬환 영어 : matrix ring )이라고 한다. 행렬환의 곱셈 항등원 은 단위 행렬
1
n
×
n
=
(
1
0
⋯
0
0
1
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
1
)
∈
Mat
(
n
;
R
)
{\displaystyle 1_{n\times n}={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}\in \operatorname {Mat} (n;R)}
이다.
행렬환은 일반적으로 가환환 이 아니다. 즉, 행렬 곱셈의 교환 법칙 은 (체 의 경우에도) 일반적으로 성립하지 않는다. 예를 들어, 실수 2×2 행렬의 경우
(
1
0
0
0
)
(
1
2
0
3
)
=
(
1
2
0
0
)
{\displaystyle {\begin{pmatrix}1&0\\0&0\end{pmatrix}}{\begin{pmatrix}1&2\\0&3\end{pmatrix}}={\begin{pmatrix}1&2\\0&0\end{pmatrix}}}
이지만
(
1
2
0
3
)
(
1
0
0
0
)
=
(
1
0
0
0
)
{\displaystyle {\begin{pmatrix}1&2\\0&3\end{pmatrix}}{\begin{pmatrix}1&0\\0&0\end{pmatrix}}={\begin{pmatrix}1&0\\0&0\end{pmatrix}}}
이다.
물론 가환 하는 두 행렬도 존재한다. 예를 들어, 가환환 위의 스칼라 행렬 은 (같은 크기의) 모든 행렬과 가환한다. 또한, 가환환
R
{\displaystyle R}
A
∈
Mat
(
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (n;R)}
R
[
A
]
=
{
p
(
A
)
:
p
∈
R
[
x
]
}
⊆
Mat
(
n
;
R
)
{\displaystyle R[A]=\{p(A)\colon p\in R[x]\}\subseteq \operatorname {Mat} (n;R)}
는 가환환 이다.
행렬환은 일반적으로 0이 아닌 왼쪽·오른쪽 영인자 를 갖는다. 즉, 0이 아닌 두 행렬의 곱은 0일 수 있으며, 소거 법칙 이 일반적으로 성립하지 않는다. 예를 들어, 실수 행렬에서
(
2
−
1
−
2
1
)
(
1
3
2
6
)
=
(
0
0
0
0
)
{\displaystyle {\begin{pmatrix}2&-1\\-2&1\end{pmatrix}}{\begin{pmatrix}1&3\\2&6\end{pmatrix}}={\begin{pmatrix}0&0\\0&0\end{pmatrix}}}
이다.
행렬환
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
가역원 은 가역 행렬 역원 은 역행렬 체 위에서도) 0이 아닌 비가역 행렬 을 갖는다. 예를 들어, 실수 2×2 정사각 행렬
(
0
5
0
3
)
{\displaystyle {\begin{pmatrix}0&5\\0&3\end{pmatrix}}}
은 가역 행렬 이 아니다.
만약
R
{\displaystyle R}
가환환 일 경우, 가역 행렬은 행렬식 이 환의 가역원인 것과 동치 이며, 특히 체 의 경우 행렬식 이 0이 아닌 것과 동치 이다. 또한, 가역 행렬
A
∈
Unit
(
Mat
(
n
;
R
)
)
{\displaystyle A\in \operatorname {Unit} (\operatorname {Mat} (n;R))}
역행렬 은 행렬식 과 수반 행렬 을 통하여 다음과 같이 나타낼 수 있다.
A
−
1
=
1
det
A
adj
A
{\displaystyle A^{-1}={\frac {1}{\det A}}\operatorname {adj} A}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
전치 행렬
A
⊤
∈
Mat
(
n
,
m
;
R
)
{\displaystyle A^{\top }\in \operatorname {Mat} (n,m;R)}
n
×
m
{\displaystyle n\times m}
i
∈
{
1
,
…
,
n
}
{\displaystyle i\in \{1,\dotsc ,n\}}
j
∈
{
1
,
…
,
m
}
{\displaystyle j\in \{1,\dotsc ,m\}}
(
A
⊤
)
i
j
=
A
j
i
{\displaystyle (A^{\top })_{ij}=A_{ji}}
이다.[ 2] :99
다음은 실수 행렬의 예다.
(
9
8
7
−
1
3
4
)
⊤
=
(
9
−
1
8
3
7
4
)
{\displaystyle {\begin{pmatrix}9&8&7\\-1&3&4\end{pmatrix}}^{\top }={\begin{pmatrix}9&-1\\8&3\\7&4\end{pmatrix}}}
이다.
전치 행렬은 함수
⊤
:
Mat
(
m
,
n
;
R
)
→
Mat
(
n
,
m
;
R
)
{\displaystyle ^{\top }\colon \operatorname {Mat} (m,n;R)\to \operatorname {Mat} (n,m;R)}
로서
(
R
,
R
)
{\displaystyle (R,R)}
쌍가군 동형 을 이루며, 그 역함수 또한 (정의역 과 공역 이 뒤바뀐) 전치 행렬이다.
또한, 임의의
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
n
×
p
{\displaystyle n\times p}
B
∈
Mat
(
n
,
p
;
R
)
{\displaystyle B\in \operatorname {Mat} (n,p;R)}
(
A
B
)
⊤
=
B
⊤
A
⊤
{\displaystyle (AB)^{\top }=B^{\top }A^{\top }}
이다.
특히, 환
R
{\displaystyle R}
R
{\displaystyle R}
결합 대수
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
전치 행렬 은
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
반대환
Mat
(
n
;
R
)
op
{\displaystyle \operatorname {Mat} (n;R)^{\operatorname {op} }}
대합
R
{\displaystyle R}
결합 대수 동형 이며, 만약
R
{\displaystyle R}
가환환 일 경우
Mat
(
n
;
R
)
{\displaystyle \operatorname {Mat} (n;R)}
R
{\displaystyle R}
대합 대수 를 이룬다.
이 부분의 본문은
대각합 입니다.
환
R
{\displaystyle R}
n
×
n
{\displaystyle n\times n}
A
∈
Mat
(
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (n;R)}
대각합
tr
A
=
∑
i
=
1
n
A
i
i
=
A
11
+
A
22
+
⋯
+
A
n
n
∈
R
{\displaystyle \operatorname {tr} A=\sum _{i=1}^{n}A_{ii}=A_{11}+A_{22}+\cdots +A_{nn}\in R}
대각합
tr
:
Mat
(
n
;
R
)
→
R
{\displaystyle \operatorname {tr} \colon \operatorname {Mat} (n;R)\to R}
는
(
R
,
R
)
{\displaystyle (R,R)}
선형 변환 을 이룬다. 또한, 임의의
A
∈
Mat
(
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (n;R)}
전치 행렬 의 대각합과 같다.
tr
(
A
⊤
)
=
tr
A
{\displaystyle \operatorname {tr} (A^{\top })=\operatorname {tr} A}
만약
R
{\displaystyle R}
가환환 일 경우, 임의의 두 행렬
A
,
B
∈
Mat
(
n
;
R
)
{\displaystyle A,B\in \operatorname {Mat} (n;R)}
tr
(
A
B
)
=
tr
(
B
A
)
{\displaystyle \operatorname {tr} (AB)=\operatorname {tr} (BA)}
이 부분의 본문은
행렬식 입니다.
가환환
R
{\displaystyle R}
n
×
n
{\displaystyle n\times n}
A
∈
Mat
(
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (n;R)}
행렬식
det
A
=
∑
σ
∈
Sym
(
n
)
sgn
σ
∏
i
=
1
n
A
i
,
σ
(
i
)
∈
R
{\displaystyle \det A=\sum _{\sigma \in \operatorname {Sym} (n)}\operatorname {sgn} \sigma \prod _{i=1}^{n}A_{i,\sigma (i)}\in R}
여기서
Sym
(
n
)
{\displaystyle \operatorname {Sym} (n)}
대칭군 이며,
sgn
σ
{\displaystyle \operatorname {sgn} \sigma }
순열의 부호 이다. 행렬
A
{\displaystyle A}
det
A
{\displaystyle \det A}
|
A
|
{\displaystyle |A|}
D
(
A
)
{\displaystyle \operatorname {D} (A)}
A
∈
Mat
(
2
;
R
)
{\displaystyle A\in \operatorname {Mat} (2;R)}
det
A
=
|
A
11
A
12
A
21
A
22
|
=
A
11
A
22
−
A
12
A
21
{\displaystyle \det A={\begin{vmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{vmatrix}}=A_{11}A_{22}-A_{12}A_{21}}
행렬식은
n
{\displaystyle n}
det
:
Mat
(
n
;
R
)
=
Mat
(
1
,
n
;
R
)
⊕
⋯
⊕
Mat
(
1
,
n
;
R
)
⏟
n
→
R
{\displaystyle \det \colon \operatorname {Mat} (n;R)=\underbrace {\operatorname {Mat} (1,n;R)\oplus \cdots \oplus \operatorname {Mat} (1,n;R)} _{n}\to R}
로서, 단위 행렬 의 상 이 1인 유일한
R
{\displaystyle R}
교대 다중 선형 형식 이다. 또한, 행렬식은 두 환의 곱셈 모노이드 사이의 준동형이며, 전치 행렬 에 대하여 불변이다. 즉, 임의의
A
,
B
∈
Mat
(
n
;
R
)
{\displaystyle A,B\in \operatorname {Mat} (n;R)}
det
(
A
B
)
=
det
A
det
B
{\displaystyle \det(AB)=\det A\det B}
det
A
⊤
=
det
A
{\displaystyle \det A^{\top }=\det A}
이다.
행렬식은 크라메르 공식 에서 사용된다.
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
A
∈
Mat
(
m
,
n
;
R
)
{\displaystyle A\in \operatorname {Mat} (m,n;R)}
I
=
{
i
1
,
i
2
,
…
,
i
|
I
|
}
⊆
{
1
,
…
,
m
}
(
i
1
<
i
2
<
⋯
<
i
|
I
|
)
{\displaystyle I=\{i_{1},i_{2},\dotsc ,i_{|I|}\}\subseteq \{1,\dotsc ,m\}\qquad (i_{1}<i_{2}<\cdots <i_{|I|})}
J
=
{
j
1
,
j
2
,
…
,
j
|
J
|
}
⊆
{
1
,
…
,
n
}
(
j
1
<
j
2
<
⋯
<
j
|
J
|
)
{\displaystyle J=\{j_{1},j_{2},\dotsc ,j_{|J|}\}\subseteq \{1,\dotsc ,n\}\qquad (j_{1}<j_{2}<\cdots <j_{|J|})}
에 속하는 행과 열을 취한 부분 행렬
A
I
,
J
=
(
A
i
1
,
j
1
A
i
1
,
j
2
⋯
A
i
1
,
j
|
J
|
A
i
2
,
j
1
A
i
2
,
j
2
⋯
A
i
2
,
j
|
J
|
⋮
⋮
⋱
⋮
A
i
|
I
|
,
j
1
A
i
|
I
|
,
j
2
⋯
A
i
|
I
|
,
j
|
J
|
)
∈
Mat
(
|
I
|
,
|
J
|
;
R
)
{\displaystyle A_{I,J}={\begin{pmatrix}A_{i_{1},j_{1}}&A_{i_{1},j_{2}}&\cdots &A_{i_{1},j_{|J|}}\\A_{i_{2},j_{1}}&A_{i_{2},j_{2}}&\cdots &A_{i_{2},j_{|J|}}\\\vdots &\vdots &\ddots &\vdots \\A_{i_{|I|},j_{1}}&A_{i_{|I|},j_{2}}&\cdots &A_{i_{|I|},j_{|J|}}\end{pmatrix}}\in \operatorname {Mat} (|I|,|J|;R)}
특히,
A
{\displaystyle A}
I
{\displaystyle I}
주부분 행렬
A
I
,
I
{\displaystyle A_{I,I}}
[ 3] :24, §1.3.3
A
{\displaystyle A}
k
×
k
{\displaystyle k\times k}
선행 주부분 행렬
A
{
1
,
…
,
k
}
,
{
1
,
…
,
k
}
{\displaystyle A_{\{1,\dotsc ,k\},\{1,\dotsc ,k\}}}
[ 3] :24, §1.3.3
A
{\displaystyle A}
i
{\displaystyle i}
행벡터
A
i
,
{
1
,
…
,
n
}
{\displaystyle A_{i,\{1,\dotsc ,n\}}}
A
{\displaystyle A}
j
{\displaystyle j}
열벡터
A
{
1
,
…
,
m
}
,
j
{\displaystyle A_{\{1,\dotsc ,m\},j}}
가환환 위의 행렬의 부분 정사각 행렬 의 행렬식 을 소행렬식
다른 뜻에 대해서는 행진 문서를 참고하십시오.
![{\displaystyle A[i,j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1a9bfca6057f52b4e5c3844ecd704962b7e426c)
이 부분의 본문은 행렬 덧셈입니다.
![{\displaystyle R[A]=\{p(A)\colon p\in R[x]\}\subseteq \operatorname {Mat} (n;R)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b38178f10a53f84623b7238d16e4646161d27563)
