내적 은 여기로 연결됩니다. 유클리드 공간 위 내적에 대해서는
스칼라곱 문서를 참고하십시오.
선형대수학 과 함수해석학 에서 내적 공간 (內積空間, 영어 : inner product space )은 두 벡터의 쌍에 스칼라를 대응시키는 일종의 함수가 주어진 벡터 공간 이다. 내적 공간 위에서는 벡터의 길이 나 각도 등의 개념을 다룰 수 있다. 스칼라곱 을 갖춘 유클리드 공간 의 일반화이다.
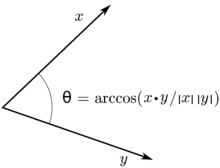
내적을 사용하여 정의한, 두 벡터 사이의 각도의 기하학적 해석
K
∈
{
R
,
C
}
{\displaystyle \mathbb {K} \in \{\mathbb {R} ,\mathbb {C} \}}
실수체 또는 복소수체 라고 하자.
K
{\displaystyle \mathbb {K} }
벡터 공간
V
{\displaystyle V}
내적 (內積, 영어 : inner product )은 양의 정부호 에르미트 반쌍선형 형식 이다. (실수 의 경우 이는 양의 정부호 대칭 쌍선형 형식 과 같다.) 즉, 다음 조건들을 만족시키는 함수
⟨
⋅
,
⋅
⟩
:
V
×
V
→
K
{\displaystyle \langle \cdot ,\cdot \rangle \colon V\times V\to \mathbb {K} }
⟨
⋅
,
⋅
⟩
:
(
u
,
v
)
↦
⟨
u
,
v
⟩
{\displaystyle \langle \cdot ,\cdot \rangle \colon (u,v)\mapsto \langle u,v\rangle }
이다.
(양의 정부호성 ) 임의의
0
≠
v
∈
V
{\displaystyle 0\neq v\in V}
⟨
v
,
v
⟩
>
0
{\displaystyle \langle v,v\rangle >0}
(에르미트성 ) 임의의
u
,
v
∈
V
{\displaystyle u,v\in V}
⟨
u
,
v
⟩
=
⟨
v
,
u
⟩
¯
{\displaystyle \langle u,v\rangle ={\overline {\langle v,u\rangle }}}
(왼쪽 선형성 ) 임의의
a
,
b
∈
K
{\displaystyle a,b\in \mathbb {K} }
u
,
v
,
w
∈
V
{\displaystyle u,v,w\in V}
⟨
a
u
+
b
v
,
w
⟩
=
a
⟨
u
,
w
⟩
+
b
⟨
v
,
w
⟩
{\displaystyle \langle au+bv,w\rangle =a\langle u,w\rangle +b\langle v,w\rangle }
이들 성질로부터 내적의 다음과 같은 성질을 유도할 수 있다.
(오른쪽 반쌍선형성 ) 임의의
a
,
b
∈
K
{\displaystyle a,b\in \mathbb {K} }
u
,
v
,
w
∈
V
{\displaystyle u,v,w\in V}
⟨
w
,
a
u
+
b
v
⟩
=
a
¯
⟨
w
,
u
⟩
+
b
¯
⟨
w
,
v
⟩
{\displaystyle \langle w,au+bv\rangle ={\bar {a}}\langle w,u\rangle +{\bar {b}}\langle w,v\rangle }
내적이 주어진
K
{\displaystyle \mathbb {K} }
(
V
,
⟨
⋅
,
⋅
⟩
)
{\displaystyle (V,\langle \cdot ,\cdot \rangle )}
K
{\displaystyle \mathbb {K} }
K
=
C
{\displaystyle \mathbb {K} =\mathbb {C} }
유니터리 공간 (영어 : unitary space )이라고 부르기도 한다.
K
{\displaystyle \mathbb {K} }
V
{\displaystyle V}
K
{\displaystyle \mathbb {K} }
노름 공간 구조를 다음과 같이 줄 수 있다.
‖
v
‖
=
⟨
v
,
v
⟩
{\displaystyle \Vert v\Vert ={\sqrt {\langle v,v\rangle }}}
노름의 양의 정부호성과 양의 동차성은 내적의 정의에 따라 자명하다. 노름의 삼각 부등식 은 코시-슈바르츠 부등식 의 따름정리이며, 그 증명은 다음과 같다. 임의의 벡터
u
,
v
∈
V
{\displaystyle u,v\in V}
‖
u
+
v
‖
2
=
‖
u
‖
2
+
2
Re
⟨
u
,
v
⟩
+
‖
v
‖
2
≤
‖
u
‖
2
+
2
‖
u
‖
‖
v
‖
+
‖
v
‖
2
=
(
‖
u
‖
+
‖
v
‖
)
2
{\displaystyle {\begin{aligned}\Vert u+v\Vert ^{2}&=\Vert u\Vert ^{2}+2\operatorname {Re} \langle u,v\rangle +\Vert v\Vert ^{2}\\&\leq \Vert u\Vert ^{2}+2\Vert u\Vert \Vert v\Vert +\Vert v\Vert ^{2}\\&=(\Vert u\Vert +\Vert v\Vert )^{2}\end{aligned}}}
이므로,
‖
u
+
v
‖
≤
‖
u
‖
+
‖
v
‖
{\displaystyle \Vert u+v\Vert \leq \Vert u\Vert +\Vert v\Vert }
반대로,
K
{\displaystyle \mathbb {K} }
노름 공간 이
K
{\displaystyle \mathbb {K} }
평행 사변형 법칙
2
‖
u
‖
2
+
2
‖
v
‖
2
=
‖
u
+
v
‖
2
+
‖
u
−
v
‖
2
∀
u
,
v
∈
V
{\displaystyle 2\Vert u\Vert ^{2}+2\Vert v\Vert ^{2}=\Vert u+v\Vert ^{2}+\Vert u-v\Vert ^{2}\qquad \forall u,v\in V}
이다. 이 경우, 가능한 유일한 내적은 다음과 같으며, 이를 극화 항등식 (極化恒等式, 영어 : polarization identity )이라고 한다.
⟨
u
,
v
⟩
=
{
1
4
‖
u
+
v
‖
2
−
1
4
‖
u
−
v
‖
2
K
=
R
1
4
‖
u
+
v
‖
2
−
1
4
‖
u
−
v
‖
2
+
i
4
‖
u
+
i
v
‖
2
−
i
4
‖
u
−
i
v
‖
2
K
=
C
{\displaystyle \langle u,v\rangle ={\begin{cases}{\frac {1}{4}}\Vert u+v\Vert ^{2}-{\frac {1}{4}}\Vert u-v\Vert ^{2}&\mathbb {K} =\mathbb {R} \\{\frac {1}{4}}\Vert u+v\Vert ^{2}-{\frac {1}{4}}\Vert u-v\Vert ^{2}+{\frac {i}{4}}\Vert u+iv\Vert ^{2}-{\frac {i}{4}}\Vert u-iv\Vert ^{2}&\mathbb {K} =\mathbb {C} \end{cases}}}
실수 내적 공간의 경우만을 증명하자. 극화 항등식이 정의한 내적이 다음 네 가지를 보이는 것으로 족하다.
⟨
v
,
v
⟩
>
0
∀
0
≠
v
∈
V
{\displaystyle \langle v,v\rangle >0\qquad \forall 0\neq v\in V}
⟨
u
,
v
⟩
=
⟨
v
,
u
⟩
∀
u
,
v
∈
V
{\displaystyle \langle u,v\rangle =\langle v,u\rangle \qquad \forall u,v\in V}
⟨
u
+
v
,
w
⟩
=
⟨
u
,
w
⟩
+
⟨
v
,
w
⟩
∀
u
,
v
,
w
∈
V
{\displaystyle \langle u+v,w\rangle =\langle u,w\rangle +\langle v,w\rangle \qquad \forall u,v,w\in V}
⟨
a
u
,
v
⟩
=
a
⟨
u
,
v
⟩
∀
a
∈
R
,
u
,
v
∈
V
{\displaystyle \langle au,v\rangle =a\langle u,v\rangle \qquad \forall a\in \mathbb {R} ,\;u,v\in V}
첫째와 둘째 조건은 자명하다. 셋째 조건은 다음과 같이 증명된다.
⟨
u
+
v
,
w
⟩
=
1
4
(
‖
u
+
v
+
w
‖
2
−
‖
u
+
v
−
w
‖
2
)
=
1
4
(
‖
u
+
w
‖
2
+
‖
v
+
w
‖
2
+
‖
u
‖
2
+
‖
v
‖
2
−
1
2
‖
u
−
v
+
w
‖
2
−
1
2
‖
v
−
u
+
w
‖
2
)
−
1
4
(
‖
u
−
w
‖
2
+
‖
v
−
w
‖
2
+
‖
u
‖
2
+
‖
v
‖
2
−
1
2
‖
u
−
v
−
w
‖
2
−
1
2
‖
v
−
u
−
w
‖
2
)
=
1
4
(
‖
u
+
w
‖
2
−
‖
u
−
v
‖
2
)
−
1
4
(
‖
v
+
w
‖
2
−
‖
v
−
w
‖
2
)
=
⟨
u
,
w
⟩
+
⟨
v
,
w
⟩
{\displaystyle {\begin{aligned}\langle u+v,w\rangle &={\frac {1}{4}}(\Vert u+v+w\Vert ^{2}-\Vert u+v-w\Vert ^{2})\\&={\frac {1}{4}}\left(\Vert u+w\Vert ^{2}+\Vert v+w\Vert ^{2}+\Vert u\Vert ^{2}+\Vert v\Vert ^{2}-{\frac {1}{2}}\Vert u-v+w\Vert ^{2}-{\frac {1}{2}}\Vert v-u+w\Vert ^{2}\right)\\&\qquad -{\frac {1}{4}}\left(\Vert u-w\Vert ^{2}+\Vert v-w\Vert ^{2}+\Vert u\Vert ^{2}+\Vert v\Vert ^{2}-{\frac {1}{2}}\Vert u-v-w\Vert ^{2}-{\frac {1}{2}}\Vert v-u-w\Vert ^{2}\right)\\&={\frac {1}{4}}(\Vert u+w\Vert ^{2}-\Vert u-v\Vert ^{2})-{\frac {1}{4}}(\Vert v+w\Vert ^{2}-\Vert v-w\Vert ^{2})\\&=\langle u,w\rangle +\langle v,w\rangle \end{aligned}}}
넷째 조건의
a
∈
N
{\displaystyle a\in \mathbb {N} }
⟨
a
u
,
v
⟩
=
⟨
u
+
⋯
+
u
⏟
a
,
v
⟩
=
⟨
u
,
v
⟩
+
⋯
+
⟨
u
,
v
⟩
⏟
a
=
a
⟨
u
,
v
⟩
{\displaystyle \langle au,v\rangle =\langle \underbrace {u+\cdots +u} _{a},v\rangle =\underbrace {\langle u,v\rangle +\cdots +\langle u,v\rangle } _{a}=a\langle u,v\rangle }
또한,
a
∈
Z
{\displaystyle a\in \mathbb {Z} }
0
=
⟨
0
,
v
⟩
=
⟨
a
u
−
a
u
,
v
⟩
=
⟨
a
u
,
v
⟩
+
⟨
−
a
u
,
v
⟩
=
⟨
a
u
,
v
⟩
−
a
⟨
u
,
v
⟩
{\displaystyle 0=\langle 0,v\rangle =\langle au-au,v\rangle =\langle au,v\rangle +\langle -au,v\rangle =\langle au,v\rangle -a\langle u,v\rangle }
만약
a
∈
Q
{\displaystyle a\in \mathbb {Q} }
a
=
p
/
q
{\displaystyle a=p/q}
p
,
q
∈
Z
,
q
≠
0
{\displaystyle p,q\in \mathbb {Z} ,\;q\neq 0}
q
⟨
a
u
,
v
⟩
=
⟨
q
a
u
,
v
⟩
=
⟨
p
u
,
v
⟩
=
p
⟨
u
,
v
⟩
{\displaystyle q\langle au,v\rangle =\langle qau,v\rangle =\langle pu,v\rangle =p\langle u,v\rangle }
마지막으로,
a
∈
R
{\displaystyle a\in \mathbb {R} }
u
,
v
∈
V
{\displaystyle u,v\in V}
a
↦
⟨
a
u
,
v
⟩
−
a
⟨
u
,
v
⟩
{\displaystyle a\mapsto \langle au,v\rangle -a\langle u,v\rangle }
내적 공간
V
{\displaystyle V}
v
∈
V
{\displaystyle v\in V}
코시-슈바르츠 부등식
|
⟨
u
,
v
⟩
|
≤
‖
u
‖
‖
v
‖
{\displaystyle |\langle u,v\rangle |\leq \Vert u\Vert \Vert v\Vert }
|
⟨
u
,
v
⟩
|
=
‖
u
‖
‖
v
‖
⟺
rank
{
u
,
v
}
<
2
{\displaystyle |\langle u,v\rangle |=\Vert u\Vert \Vert v\Vert \iff \operatorname {rank} \{u,v\}<2}
이에 따라, 두 벡터
u
,
v
∈
V
{\displaystyle u,v\in V}
arccos
Re
⟨
u
,
v
⟩
‖
u
‖
‖
v
‖
{\displaystyle \arccos {\frac {\operatorname {Re} \langle u,v\rangle }{\Vert u\Vert \Vert v\Vert }}}
또한, 내적이 유도하는 노름의 삼각 부등식 은 코시-슈바르츠 부등식을 통해 증명된다.
내적 공간
V
{\displaystyle V}
정규 직교 기저 (正規直交基底, 영어 : orthonormal basis )는 서로 다른 두 벡터의 내적이 항상 0인 단위 벡터들이 이루는 기저 이다. 즉, 이는 다음 조건들을 만족시키는 기저
B
⊆
V
{\displaystyle B\subseteq V}
(직교성) 만약
e
,
e
′
∈
B
{\displaystyle e,e'\in B}
e
≠
e
′
{\displaystyle e\neq e'}
⟨
e
,
e
′
⟩
=
0
{\displaystyle \langle e,e'\rangle =0}
(정규성) 임의의
e
∈
B
{\displaystyle e\in B}
‖
e
‖
=
1
{\displaystyle \Vert e\Vert =1}
유한 차원 내적 공간의 정규 직교 기저는 항상 존재한다. 이는 그람-슈미트 과정 을 통해 구성할 수 있다.
내적 공간
V
{\displaystyle V}
v
∈
V
{\displaystyle v\in V}
B
{\displaystyle B}
v
=
∑
e
∈
B
⟨
v
,
e
⟩
e
{\displaystyle v=\sum _{e\in B}\langle v,e\rangle e}
또한, 이 좌표 아래 내적을 다음과 같이 나타낼 수 있다.
⟨
u
,
v
⟩
=
∑
e
∈
B
⟨
u
,
e
⟩
⟨
v
,
e
⟩
¯
{\displaystyle \langle u,v\rangle =\sum _{e\in B}\langle u,e\rangle {\overline {\langle v,e\rangle }}}
내적 공간
V
{\displaystyle V}
S
⊆
V
∖
{
0
}
{\displaystyle S\subseteq V\setminus \{0\}}
v
∈
V
{\displaystyle v\in V}
베셀 부등식 과 유사한 꼴의 다음과 같은 부등식이 성립한다.
∑
e
∈
S
|
⟨
v
,
e
⟩
|
2
≤
‖
v
‖
2
{\displaystyle \sum _{e\in S}|\langle v,e\rangle |^{2}\leq \Vert v\Vert ^{2}}
∑
e
∈
S
|
⟨
v
,
e
⟩
|
2
=
‖
v
‖
2
⟺
v
=
∑
e
∈
S
⟨
v
,
e
⟩
e
{\displaystyle \sum _{e\in S}|\langle v,e\rangle |^{2}=\Vert v\Vert ^{2}\iff v=\sum _{e\in S}\langle v,e\rangle e}
유한 차원 내적 공간
V
{\displaystyle V}
선형 범함수 는 어떤 유일한 고정된 벡터
v
∈
V
{\displaystyle v\in V}
V
→
K
{\displaystyle V\to \mathbb {K} }
u
↦
⟨
u
,
v
⟩
{\displaystyle u\mapsto \langle u,v\rangle }
이다. 구체적으로, 정규 직교 기저
B
⊆
V
{\displaystyle B\subseteq V}
f
:
V
→
F
{\displaystyle f\colon V\to F}
v
=
∑
e
∈
B
f
(
e
)
¯
e
{\displaystyle v=\sum _{e\in B}{\overline {f(e)}}e}
이에 따라, 유한 차원 내적 공간의 선형 변환
T
:
V
→
V
{\displaystyle T\colon V\to V}
수반 선형 변환
T
∗
:
V
→
V
{\displaystyle T^{*}\colon V\to V}
⟨
T
u
,
v
⟩
=
⟨
u
,
T
∗
v
⟩
∀
u
,
v
∈
V
{\displaystyle \langle Tu,v\rangle =\langle u,T^{*}v\rangle \qquad \forall u,v\in V}
그러나 무한 차원 내적 공간의 경우 일반적으로 성립하지 않는다. 예를 들어, 다항식환
C
[
x
]
{\displaystyle \mathbb {C} [x]}
⟨
p
,
q
⟩
=
∫
a
b
p
(
x
)
q
(
x
)
¯
d
x
=
∑
k
=
0
deg
p
∑
k
′
=
0
deg
q
p
k
q
k
′
¯
k
+
k
′
+
1
{\displaystyle \langle p,q\rangle =\int _{a}^{b}p(x){\overline {q(x)}}dx=\sum _{k=0}^{\deg p}\sum _{k'=0}^{\deg q}{\frac {p_{k}{\overline {q_{k'}}}}{k+k'+1}}}
이 경우, 임의의
c
∈
C
{\displaystyle c\in \mathbb {C} }
C
[
x
]
→
C
{\displaystyle \mathbb {C} [x]\to \mathbb {C} }
p
↦
p
(
c
)
{\displaystyle p\mapsto p(c)}
또한 미분 선형 변환
D
:
C
[
x
]
→
C
[
x
]
{\displaystyle D\colon \mathbb {C} [x]\to \mathbb {C} [x]}
D
:
x
n
↦
n
x
n
−
1
n
=
0
,
1
,
2
,
…
{\displaystyle D\colon x^{n}\mapsto nx^{n-1}\qquad n=0,1,2,\dots }
의 수반 선형 변환은 존재하지 않는다.
n
{\displaystyle n}
K
{\displaystyle \mathbb {K} }
벡터 공간
K
n
{\displaystyle \mathbb {K} ^{n}}
⟨
x
,
y
⟩
=
∑
k
=
1
n
x
k
y
k
¯
{\displaystyle \langle x,y\rangle =\sum _{k=1}^{n}x_{k}{\overline {y_{k}}}}
K
=
R
{\displaystyle \mathbb {K} =\mathbb {R} }
R
n
{\displaystyle \mathbb {R} ^{n}}
유클리드 공간 이며, 이 내적은 스칼라곱 이라고 부른다. 이 경우 실수의 켤레 복소수 는 스스로와 일치한다 (
y
k
¯
=
y
k
{\displaystyle {\overline {y_{k}}}=y_{k}}
L2 노름 이다. 그러나
p
≠
2
{\displaystyle p\neq 2}
Lp 노름 은 평행 사변형 법칙을 만족시키지 않으므로 내적으로부터 유도될 수 없다.
특히,
n
=
1
{\displaystyle n=1}
K
{\displaystyle \mathbb {K} }
⟨
x
,
y
⟩
=
x
y
¯
{\displaystyle \langle x,y\rangle =x{\overline {y}}}
이다.
마찬가지로, 실수 또는 복소수 성분 행렬들의 집합
Mat
(
m
,
n
;
K
)
{\displaystyle \operatorname {Mat} (m,n;\mathbb {K} )}
m
n
{\displaystyle mn}
벡터 공간 을 이룬다. 이 위에 다음과 같은 내적을 정의할 수 있다.
⟨
X
,
Y
⟩
=
tr
(
X
†
Y
¯
)
=
∑
i
=
1
m
∑
j
=
1
n
X
i
j
Y
i
j
¯
{\displaystyle \langle X,Y\rangle =\operatorname {tr} (X^{\dagger }{\bar {Y}})=\sum _{i=1}^{m}\sum _{j=1}^{n}X_{ij}{\overline {Y_{ij}}}}
이를 프로베니우스 내적 이라고 한다.
보다 일반적으로, 양의 정부호 행렬
M
∈
Mat
(
n
,
n
;
K
)
{\displaystyle M\in \operatorname {Mat} (n,n;\mathbb {K} )}
K
n
{\displaystyle \mathbb {K} ^{n}}
⟨
x
,
y
⟩
=
x
T
M
y
¯
=
∑
i
=
1
n
∑
j
=
1
n
M
i
j
x
i
y
j
¯
{\displaystyle \langle x,y\rangle =x^{\operatorname {T} }M{\bar {y}}=\sum _{i=1}^{n}\sum _{j=1}^{n}M_{ij}x_{i}{\overline {y_{j}}}}
연속 함수 의 공간
C
(
[
a
,
b
]
;
K
)
{\displaystyle {\mathcal {C}}([a,b];\mathbb {K} )}
⟨
f
,
g
⟩
=
∫
a
b
f
(
x
)
g
(
x
)
¯
d
x
{\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x){\overline {g(x)}}dx}
여기서 우변의 적분은 리만 적분 이다. 또한, 다음과 같은 내적을 정의할 수도 있다.
⟨
f
,
g
⟩
=
∫
a
b
x
2
f
(
x
)
g
(
x
)
¯
d
x
{\displaystyle \langle f,g\rangle =\int _{a}^{b}x^{2}f(x){\overline {g(x)}}dx}
가측 함수
(
Ω
,
Σ
,
μ
)
→
K
{\displaystyle (\Omega ,\Sigma ,\mu )\to \mathbb {K} }
거의 어디서나 같음에 대한) 동치류 들로 구성된
K
{\displaystyle \mathbb {K} }
벡터 공간
L
2
(
Ω
;
K
)
{\displaystyle \operatorname {L} ^{2}(\Omega ;\mathbb {K} )}
⟨
f
,
g
⟩
=
∫
a
b
f
g
¯
d
μ
{\displaystyle \langle f,g\rangle =\int _{a}^{b}f{\overline {g}}d\mu }
여기서 우변은 르베그 적분 이다. 이를 L2 공간 이라고 한다. 특히,
(
Ω
,
Σ
,
μ
)
{\displaystyle (\Omega ,\Sigma ,\mu )}
확률 공간 일 때,
L
2
(
Ω
;
K
)
{\displaystyle \operatorname {L} ^{2}(\Omega ;\mathbb {K} )}
확률 변수 들의 동치류 들로 이루어지며, 적분은 기댓값 이다. 따라서, 두 확률 변수
X
,
Y
:
Ω
→
K
{\displaystyle X,Y\colon \Omega \to \mathbb {K} }
⟨
X
,
Y
⟩
=
E
(
X
Y
¯
)
{\displaystyle \langle X,Y\rangle =\operatorname {E} (X{\overline {Y}})}
가측 함수나 확률 변수의 동치류를 취하는 것은 내적을 양의 정부호적이게 만들기 위함이다. 예를 들어,
⟨
X
,
X
⟩
=
0
{\displaystyle \langle X,X\rangle =0}
필요충분조건 은 거의 확실하게
X
=
0
{\displaystyle X=0}
μ
(
X
=
0
)
=
1
{\displaystyle \mu (X=0)=1}