사용자:IcyPot/이상 적분

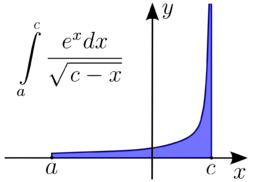
해석학에서 이상 적분(異常積分, 영어: improper integral)은 정적분에서 요구하는 가정이 성립하지 않는 경우에 대해 정의된 정적분의 확장된 개념이다.

1종 이상 리만 적분은 적분이 나타내는 평면 상의 영역이 수평적으로 무한한 경우를 의미한다. 이러한 영역의 면적, 즉 적분이 나타내는 면적은 유한(그림처럼)할 수도 있고 무한할 수도 있다.

2종 이상 리만 적분은 적분이 나타내는 영역이 수직으로 무한한 경우를 의미한다. 이 영역의 면적은 유한(그림처럼)할 수도 있고 무한할 수도 있다.

리만 적분(또는 다르부 적분)에서 , 이는 정적분에서 적분 구간이 무한하거나, 적분함수 자체가 무한한 경우(즉, 함수가 발산하는 경우) 또는 그 두 가지 모두에 해당할 때 발생한다.

또한 유계이지만 닫혀있지 않은 집합이나, 유계이지만 연속적이지 않은 함수에 대해서도 적용될 수 있다.

이상적분은 보통 일반적인 정적분과 동일하게 표기되지만, 실제로는 정적분의 극한 또는 극한들의 합을 나타낸다. 따라서 이상적분은 수렴하거나 발산한다고 말한다. 정적분을 이상적분으로 계산하더라도 동일한 결과를 얻게 된다.

가장 간단한 경우로, 하나의 구간에서 하나의 변수를 갖는 실수값 함수가 리만(또는 다르부)적분되는 상황에서, 이상적분은 다음과 같은 형태로 나타낼 수 있다.

$\int _{a}^{\infty }f(x)dx$
$\int _{-\infty }^{b}f(x)dx$
$\int _{-\infty }^{\infty }f(x)dx$
$\int _{a}^{b}f(x)dx$ , 함수가 구간 [a, b] 사이에서 정의되지 않거나 불연속적인 점을 가지는 경우

처음 세 가지 형태의 적분은 적분 구간이 무한하기 때문에 이상적분이다.(이외에도 다른 이유로 이상적분이 될 수 있다.) 이러한 적분은 때때로 "첫 번째 종류" 또는 "1종 이상적분"이라고 불리며, 이는 피적분함수가 적분의 조건을 충족하는 경우이다.

네 번째 형태의 적분은 함수 f(x)가 구간 [a, b] 내에서 수직 점근선을 가지므로 이상적분인데, 이는 "두 번째 종류" 또는 "2종 이상적분"이라고 설명될 수 있다.

두 가지 종류의 요소를 모두 결합한 적분은 때때로 "세 번째 종류" 또는 "3종 이상적분"이라고도 한다.

위의 각 경우에서, 적분이 이상적분이 되는 원인에 따라 하나 이상의 극한을 사용하여 적분을 다시 작성해야 한다. 예를 들어, 첫 번째 형태의 적분에서 함수 $f(x)$ 가 구간 $[a,\infty )$ 에서 연속적이라면, 다음과 같이 표현한다.

$\int _{a}^{\infty }f(x)dx=\lim _{b\to \infty }\int _{a}^{b}f(x)dx$

오른쪽의 극한이 왼쪽 적분의 정의로 간주된다.

만약 함수 $f(x)$ 가 구간 $[a,\infty )$ 에서만 연속적이고, a에서 연속적이지 않다면, 이는 보통 다음과 같이 다시 작성한다.

$\int _{a}^{\infty }f(x)dx=\lim _{t\to a^{+}}\int _{t}^{c}f(x)dx+\lim _{b\to \infty }\int _{c}^{b}f(x)dx$ ,

어떤 $c>a$ 를 선택하더라도, 여기서 두 극한 모두가 유한한 값으로 수렴해야 이상적분이 수렴한다고 할 수 있다. 이러한 조건은 양의 무한대와 음의 무한대를 더하는 애매한 상황(즉, " $\infty -\infty$ "의 부정형)을 방지하기 위함이다.

대안으로, 반복 극한을 사용하거나 코시 주요값에 기반한 단일 극한을 사용할 수 있다.

정의

실수 구간에 정의된 실숫값 함수

f\colon [a,b]\setminus \{-\infty ,\infty \}\to \mathbb {R} \qquad (-\infty \leq a<b\leq \infty )

에 대하여, 다음을 만족시키는 $n\in \mathbb {N}$ 및 $a=c_{0}<c_{1}<\cdots <c_{n}=b$ 가 존재한다고 하자.

임의의 $k=1,2,\dots ,n$ 및 $[\gamma _{k},\delta _{k}]\subseteq (c_{k-1},c_{k})$ 에 대하여, $\int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x\in \mathbb {R}$ 가 존재한다.

그렇다면, $f$ 의 이상 적분은 다음과 같은 극한이다.

{\begin{aligned}\int _{a}^{b}f(x)\mathrm {d} x&=\lim _{\gamma _{1}\to c_{0}+0}\lim _{\delta _{1}\to c_{1}-0}\cdots \lim _{\gamma _{n}\to c_{n-1}+0}\lim _{\delta _{n}\to c_{n}-0}\sum _{k=1}^{n}\int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x\\&=\sum _{k=1}^{n}\left(\lim _{\gamma _{k}\to c_{k-1}+0}\int _{\gamma _{k}}^{\frac {x_{k-1}+x_{k}}{2}}f(x)\mathrm {d} x+\lim _{\delta _{k}\to c_{k}-0}\int _{\frac {x_{k-1}+x_{k}}{2}}^{\delta _{k}}f(x)\mathrm {d} x\right)\end{aligned}}

물론 이상 적분은 존재하지 않을 수 있다. 존재한다면, 이상 적분이 수렴(收斂)한다고 하며, 존재하지 않는다면, 이상적분이 발산(發散)한다고 한다. 함수의 절댓값의 이상 적분

\int _{a}^{b}|f(x)|\mathrm {d} x

의 수렴은 원래 이상 적분의 수렴보다 더 강한 조건이다. 절댓값의 이상 적분이 수렴한다면, 원래 이상 적분이 절대 수렴(絶對收斂)한다고 한다. 수렴하지만 절대 수렴하지 않는 이상 적분을 조건 수렴(條件收斂)한다고 한다.

특이 적분

특히, 실수 함수 $f\colon [a,b)\to \mathbb {R} \qquad (-\infty <a<b\leq \infty )$ 가 임의의 $[a,\beta ]\subseteq [a,b)$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\beta \to b-0}\int _{a}^{\beta }f(x)\mathrm {d} x

마찬가지로, 실수 함수 $f\colon (a,b]\to \mathbb {R} \qquad (-\infty \leq a<b<\infty )$ 가 임의의 $[\alpha ,b]\subseteq (a,b]$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\int _{\alpha }^{b}f(x)\mathrm {d} x

또한, 실수 함수 $f\colon (a,b)\to \mathbb {R} \qquad (-\infty \leq a<b\leq \infty )$ 가 임의의 $[\alpha ,\beta ]\subseteq (a,b)$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\lim _{\beta \to b-0}\int _{\alpha }^{\beta }f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\int _{\alpha }^{\frac {a+b}{2}}f(x)\mathrm {d} x+\lim _{\beta \to b-0}\int _{\frac {a+b}{2}}^{\beta }f(x)\mathrm {d} x

또한, 실수 함수 $f\colon [a,b]\to \mathbb {R} \qquad (-\infty <a<c<b<\infty )$ 가 임의의 $[a,\delta ]\subseteq [a,c)$ 및 $[\gamma ,b]\subseteq (c,b]$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\delta \to c-0}\lim _{\gamma \to c+0}\left(\int _{a}^{\delta }f(x)\mathrm {d} x+\int _{\gamma }^{b}f(x)\mathrm {d} x\right)=\lim _{\delta \to c-0}\int _{a}^{\delta }f(x)\mathrm {d} x+\lim _{\gamma \to c+0}\int _{\gamma }^{b}f(x)\mathrm {d} x

위와 같은 여러 경우에, 만약 피적분 함수가 직접 적분하지 못하는 곳의 임의의 근방에서 무계 함수라면, 그 이상 적분을 특이 적분(特異積分, 영어: singular integral)이라고 한다.

무한대 적분

특히, 실수 함수 $f\colon [a,\infty )\to \mathbb {R} \qquad (a\in \mathbb {R} )$ 가 임의의 $[a,\beta ]\subseteq [a,\infty )$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{a}^{\infty }f(x)\mathrm {d} x=\lim _{\beta \to \infty }\int _{a}^{\beta }f(x)\mathrm {d} x

마찬가지로, 실수 함수 $f\colon (-\infty ,b]\to \mathbb {R} \qquad (b\in \mathbb {R} )$ 가 임의의 $[\alpha ,b]\subseteq (-\infty ,b]$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{-\infty }^{b}f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\int _{\alpha }^{b}f(x)\mathrm {d} x

또한, 실수 함수 $f\colon \mathbb {R} \to \mathbb {R}$ 가 임의의 $[\alpha ,\beta ]\subseteq \mathbb {R}$ 위의 적분 가능 함수라고 할 때, $f$ 의 이상 적분은 다음과 같은 극한이다.

\int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\lim _{\beta \to \infty }\int _{\alpha }^{\beta }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\int _{\alpha }^{0}f(x)\mathrm {d} x+\lim _{\beta \to \infty }\int _{0}^{\beta }f(x)\mathrm {d} x

이와 같이 적분 상한이 양의 무한대이거나, 적분 하한이 음의 무한대인 이상 적분을 무한대 적분(無限大積分)이라고 한다.

코시 주요값

(수렴하지 않을 수 있는) 이상 적분에 대하여 코시 주요값(Cauchy主要-, 영어: Cauchy principal value) 또는 코시 주치(Cauchy主値)라 불리는 값을 줄 수 있다. 즉, 이상 적분

\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\gamma _{1}\to c_{0}+0}\lim _{\delta _{1}\to c_{1}-0}\cdots \lim _{\gamma _{n}\to c_{n-1}+0}\lim _{\delta _{n}\to c_{n}-0}\sum _{k=1}^{n}\int _{\gamma _{k}}^{\delta _{k}}f(x)\mathrm {d} x

의 코시 주요값은

\operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\sum _{k=1}^{n}\int _{c_{k-1}+\epsilon }^{c_{k}-\epsilon }f(x)\mathrm {d} x

이다. 특수한 경우의 이상 적분의 코시 주요 값은 다음과 같다.

이상 적분	코시 주요값
$\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\alpha \to a+0}\lim _{\beta \to b-0}\int _{\alpha }^{\beta }f(x)\mathrm {d} x$	$\operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\int _{a+\epsilon }^{b-\epsilon }f(x)\mathrm {d} x$
$\int _{a}^{b}f(x)\mathrm {d} x=\lim _{\delta \to c-0}\lim _{\gamma \to c+0}\left(\int _{a}^{\delta }f(x)\mathrm {d} x+\int _{\gamma }^{b}f(x)\mathrm {d} x\right)$	$\operatorname {PV} \int _{a}^{b}f(x)\mathrm {d} x=\lim _{\epsilon \to 0+0}\left(\int _{a}^{c-\epsilon }f(x)\mathrm {d} x+\int _{c+\epsilon }^{b}f(x)\mathrm {d} x\right)$
$\int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\alpha \to -\infty }\lim _{\beta \to \infty }\int _{\alpha }^{\beta }f(x)\mathrm {d} x$	$\operatorname {PV} \int _{-\infty }^{\infty }f(x)\mathrm {d} x=\lim _{\gamma \to \infty }\int _{-\gamma }^{\gamma }f(x)\mathrm {d} x$

주요 적분의 이상 적분

리만 적분

(이상 적분을 사용하지 않는) 리만 적분은 유계 함수의 유계 구간 위의 적분에 제한된다. 그러나, 이상 적분을 사용하는 리만 적분은 무계 함수의 적분이나, 무계 구간 위의 적분이 일부 허용된다. 리만 적분은 르베그 적분보다 좁은 의미의 적분이나, 이상 적분을 사용하는 리만 적분은 르베그 적분에서만 가능했던 적분이 일부 허용되며, 르베그 적분에서 불가능한 적분 역시 일부 허용된다.