고등학교 수학
수학I : 공통 교육과정 기간인 중학교 3학년까지의 수학을 이수한 후 보다 높은 수준의 수학을 학습하기 위하여 선택할 수 있는 기본 과목이다. 목표 : 다항식, 방정식과 부등식, 도형의 방정식에 관련된 개념, 원리, 법칙과 이들 사이의 관계를 이해 수학II : 공통 교육과정 기간인 중학교 3학년까지의 수학과 수학I의 내용을 이해한 학생이 보다 높은 수준의 수학을 학습하기 위하여 선택할 수 있는 기본 과목이다. 목표 : 집합과 명제, 함수, 수열, 지수와 로그에 관련된 개념, 원리, 법칙과 이들 사이의 관계를 이해 미적분I : 수학I과 수학II의 내용을 이해한 학생이 선택할 수 있는 과목이다. 목표 : 수열의 극한, 함수의 극한과 연속, 다항함수의 미분법, 다항함수의 적분법에 관련된 개념, 원리, 법칙과 이들사이의 관계를 이해 미적분II : 미적분I의 내용을 이해한 학생이 선택할 수 있는 과목으로 대학의 자연계열 또는 공학계열 등의 미적분의 내용을 필요로 하는 분야로 진학하려는 학생이 이수하기에 알맞은 과목이다. 목표 : 지수함수와 로그함수, 삼각함수, 미분법, 적분법에 관련된 개념, 원리, 법칙과 이들 사이의 관계를 이해 확률과 통계 : 미적분I이나 미적분II의 내용을 이해한 학생이 선택하는 것이 바람직하지만, 미적분I이나 미적분II를 이수하지 않은 학생도 선택할 수 있는 과목이다. 목표 : 순열과 조합, 확률, 통계에 관련된 개념, 원리, 법칙과 이들 사이의 관계를 이해하는 능력을 기른다. 기하와 벡터 : 미적분I이나 미적분II의 내용을 이해한 학생이 보다 높은 수준의 수학을 학습하기 위하여 선택할수 있는 과목이다. 목표 : 평면 곡선, 평면벡터, 공간도형과 공간벡터에 관련된 개념, 원리, 법칙과 이들 사이의 관계를 이해 수학 I : 다항식, 방정식과 부등식, 도형의 방정식
수학II : 집합과 명제, 함수, 수열, 지수와 로그 내용별 :
미적분I : 수열의 극한, 함수의 극한과 연속, 다항함수의 미분법, 다항함수의 적분법
미적분II : 지수함수와 로그함수, 삼각함수, 미분법, 적분법
확률과 통계 : 순열과 조합, 확률, 통계
기하와 벡터 : 평면 곡선, 평면벡터, 공간도형과 공간벡터 다항식 (polynomial)은 일반적으로
7
x
3
+
(
−
x
2
)
+
14
x
+
(
−
3
y
2
)
+
y
+
(
−
9
)
{\displaystyle 7x^{3}+(-x^{2})+14x+(-3y^{2})+y+(-9)}
항 들의 합으로 이루어진 식을 말한다.
다항식에 있는 문자가 한두 개가 아닐 수 있으므로, 초점이 되는 '특정한 문자'가 무엇인지 알려주기 위해 (특정한 문자)에 대한 다항식 이라고 표현한다. 예를 들어 위의 다항식은 '
x
{\displaystyle x}
y
{\displaystyle y}
x에 대한 다항식
(
7
x
3
)
+
(
−
x
2
)
+
(
14
x
)
+
(
−
3
y
2
+
y
−
9
)
{\displaystyle (7x^{3})+(-x^{2})+(14x)+(-3y^{2}+y-9)}
항 이라고 한다. 다항식의 항 들 중에서 특정한 문자(위 다항식에서는 x가 된다)의 차수 가 가장 높은 항이 있을때, 그 항의 차수가 그 다항식의 차수가 된다.
예시로 제시한 위의 다항식은 x에 대한 삼차다항식이다. 또한 (특정한 문자)를 포함하지않는 항(
−
3
y
2
+
y
−
9
{\displaystyle -3y^{2}+y-9}
상수항 으로 따로 지칭하여 부른다.
단항식 이란
2
x
,
3
x
y
2
{\displaystyle 2x,3xy^{2}}
정수
n
{\displaystyle n}
0
{\displaystyle 0}
a
0
,
a
1
,
⋯
,
a
n
{\displaystyle a_{0},a_{1},\cdots ,a_{n}}
n
+
1
{\displaystyle n+1}
실수 혹은 복소수 인 상수일 때, 변수
x
{\displaystyle x}
a
0
,
a
1
,
⋯
,
a
n
{\displaystyle a_{0},a_{1},\cdots ,a_{n}}
P
(
x
)
=
a
n
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
1
x
+
a
0
=
∑
k
=
0
n
a
k
x
k
(
x
0
=
1
)
{\displaystyle P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=\sum _{k=0}^{n}{a_{k}x^{k}}\quad (x^{0}=1)}
를 변수
x
{\displaystyle x}
(univariate polynomial with constant coefficient with respect to
x
{\displaystyle x}
x
{\displaystyle x}
x
{\displaystyle x}
a
m
≠
0
{\displaystyle a_{m}\neq 0}
m
{\displaystyle m}
P
(
x
)
{\displaystyle P(x)}
차수 (次數, degree)라고 하며
deg
P
=
m
{\displaystyle \deg P=m}
다항식
P
(
x
)
{\displaystyle P(x)}
a
k
x
k
{\displaystyle a_{k}x^{k}}
항 (項, terms)이 하며,
k
{\displaystyle k}
차수 라 한다. 혹은, 다항식
P
(
x
)
{\displaystyle P(x)}
k
{\displaystyle k}
a
k
x
k
{\displaystyle a_{k}x^{k}}
m
=
deg
P
{\displaystyle m=\deg P}
m
{\displaystyle m}
a
m
x
m
{\displaystyle a_{m}x^{m}}
P
(
x
)
{\displaystyle P(x)}
최고차항 (最高次項, leading term)이라 한다.변수
x
{\displaystyle x}
x
k
{\displaystyle x^{k}}
a
k
{\displaystyle a_{k}}
x
k
{\displaystyle x^{k}}
계수 (係数, coefficient)라 한다.
x
{\displaystyle x}
0
{\displaystyle 0}
a
0
{\displaystyle a_{0}}
상수항 (constant term )이라 한다. 상수 하나는 상수항으로만 이루어진 다항식이라 할 수 있다.추상대수학에서,
x
{\displaystyle x}
P
(
x
)
{\displaystyle P(x)}
a
i
{\displaystyle a_{i}}
환
K
{\displaystyle K}
P
(
x
)
{\displaystyle P(x)}
K
[
x
]
{\displaystyle K[x]}
R
[
x
]
{\displaystyle \mathbb {R} [x]}
C
[
x
]
{\displaystyle \mathbb {C} [x]}
K
{\displaystyle K}
가환환 이면 집합
K
[
x
]
{\displaystyle K[x]}
K
{\displaystyle K}
일반적으로 다항 방정식
∑
i
=
0
n
a
i
x
i
=
0
{\displaystyle \sum _{i=0}^{n}a_{i}x^{i}=0}
의 해는 다음과 같이 구한다.
∑
i
=
0
n
a
i
x
i
{\displaystyle \sum _{i=0}^{n}a_{i}x^{i}}
인수 분해 하여
a
n
∏
j
=
1
n
(
x
−
b
i
)
{\displaystyle a_{n}\prod _{j=1}^{n}(x-b_{i})}
a
n
∏
j
=
1
n
(
x
−
b
j
)
=
0
{\displaystyle a_{n}\prod _{j=1}^{n}(x-b_{j})=0}
{
b
k
{\displaystyle b_{k}}
k
{\displaystyle k}
n
{\displaystyle n}
이므로, 위 방정식의 해도 이와 같다.
함수를 다음과 같이 방정식으로 변환하면
0.5
x
−
y
=
−
2
{\displaystyle 0.5x-y=-2}
x
+
y
=
5
{\displaystyle x+y=5}
연립방정식의 해를 구하기 위해 두 방정식을 더하면
1.5
x
=
3
{\displaystyle 1.5x=3}
x
=
3
/
1.5
=
2
{\displaystyle x=3/1.5=2}
y
=
3
{\displaystyle y=3}
이 연립방정식의 해는 그래프의 교차점의 좌표 (2,3) 이다.
그림의 이차함수
y
=
x
2
−
x
−
2
=
(
x
+
1
)
(
x
−
2
)
{\displaystyle y=x^{2}-x-2=(x+1)(x-2)}
의 그래프에서 x 축과 만나는 점의 x 좌표
x
=
−
1
,
2
{\displaystyle x=-1,2}
x
2
−
x
−
2
=
0
{\displaystyle x^{2}-x-2=0}
이라는 이차방정식의 해가 된다.
x절편은 y = 0 이므로 위에서 구한 이차방정식의 해와 같다.
y절편은
x
=
0
{\displaystyle x=0}
y
=
−
2
{\displaystyle y=-2}
가 된다.
일차 방정식(Linear equation) 또는 선형 방정식은 최고차항의 차수가 1인 방정식을 뜻한다.
방정식
2
x
+
5
−
4
x
=
−
3
x
+
45
{\displaystyle 2x+5-4x=-3x+45}
−
2
x
+
5
=
−
3
x
+
45
{\displaystyle -2x+5=-3x+45}
이때
−
3
x
{\displaystyle -3x}
5
{\displaystyle 5}
x
=
40
{\displaystyle x=40}
x
{\displaystyle x}
1
{\displaystyle 1}
일차 방정식의 해는
a
x
=
b
{\displaystyle ax=b}
a
=
0
{\displaystyle a=0}
b
≠
0
{\displaystyle b\neq 0}
2
x
−
5
+
4
x
=
3
x
−
6
+
3
x
,
6
x
−
5
=
6
x
−
6
{\displaystyle 2x-5+4x=3x-6+3x,6x-5=6x-6}
0
x
=
−
1
{\displaystyle 0x=-1}
일차 방정식의 해는
a
x
=
b
{\displaystyle ax=b}
a
=
0
{\displaystyle a=0}
b
=
0
{\displaystyle b=0}
x
−
3
+
2
x
=
7
x
+
8
−
4
x
−
11
,
3
x
−
3
=
3
x
−
3
{\displaystyle x-3+2x=7x+8-4x-11,3x-3=3x-3}
0
x
=
0
{\displaystyle 0x=0}
이차 방정식 (영어 : quadratic equation )이란, 최고차항의 차수 가 2인 다항 방정식 을 뜻한다.
x
{\displaystyle x}
a
x
2
+
b
x
+
c
=
0
,
a
≠
0
{\displaystyle ax^{2}+bx+c=0,\quad a\neq 0}
와 같고, 여기서
x
{\displaystyle x}
변수 ,
a
{\displaystyle a}
b
{\displaystyle b}
x
2
,
x
{\displaystyle x^{2},x}
계수 라고 하며,
c
{\displaystyle c}
다음은 이차 방정식의 일반적인 해법인 근의 공식이다. 그 사용법은 다음과 같다.
a
x
2
+
b
x
+
c
=
0
{\displaystyle ax^{2}+bx+c=0}
단,
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
실수 이고
a
{\displaystyle a}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
x
1
,
2
=
−
b
±
b
2
−
4
a
c
2
a
{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}}
이다.
여기에서 제곱근 기호 안의 수, 즉
D
=
b
2
−
4
a
c
{\displaystyle D=b^{2}-4ac}
를 이 이차방정식의 판별식이라고 한다.
판별식의 값에 따라 방정식의 해는 세 가지로 나뉜다.
만약 판별식이 양수이면, 방정식은 서로 다른 두 실근을 갖는다.
만약 판별식이 0이면, 방정식은 한 개의 실근을 갖는다. 이 때의 실근을 중근 이라고 한다.
만약 판별식이 음수이면, 방정식은 서로 다른 두 허근을 갖는다. 따라서, 실수 범위 내에서는 해가 존재하지 않는다. 삼차 방정식 이란, 최고차항의 차수가 3인 다항 방정식 을 뜻한다. 일반적인 모양은 다음과 같다.
a
x
3
+
b
x
2
+
c
x
+
d
=
0
,
a
≠
0
{\displaystyle ax^{3}+bx^{2}+cx+d=0,a\neq 0}
여기에서
a
,
b
,
c
{\displaystyle a,b,c}
x
3
,
x
2
,
x
{\displaystyle x^{3},x^{2},x}
계수 라고 한다.
d
{\displaystyle d}
상수항 이다.
삼차방정식에서 실근은 '서로 다른 실근 3개', '서로 다른 실근 2개 (하나는 이중근)', '실근 하나'와 같은 경우가 존재한다. 여기서 근의 개수가 몇 개인지를 알아보고자 할 때, 삼차방정식을 미분하여 생긴 이차방정식을 분석함으로써 이를 알아낼 수 있다.
삼차방정식
f
(
x
)
=
{\displaystyle f(x)=}
d
d
x
f
(
x
)
=
a
x
2
+
b
x
+
c
{\displaystyle {\frac {d}{dx}}f(x)=ax^{2}+bx+c}
이차함수의 판별식
D
=
b
2
−
4
a
c
{\displaystyle D=b^{2}-4ac}
D
>
0
{\displaystyle D>0}
f
(
x
)
=
0
{\displaystyle f(x)=0}
α
,
β
{\displaystyle \alpha ,\beta }
f
(
α
)
f
(
β
)
>
0
{\displaystyle f(\alpha )f(\beta )>0}
f
(
α
)
f
(
β
)
=
0
{\displaystyle f(\alpha )f(\beta )=0}
f
(
α
)
f
(
β
)
<
0
{\displaystyle f(\alpha )f(\beta )<0}
D
=
0
{\displaystyle D=0}
d
d
x
f
(
x
)
=
0
{\displaystyle {\frac {d}{dx}}f(x)=0}
γ
{\displaystyle \gamma }
f
(
γ
)
=
0
{\displaystyle f(\gamma )=0}
f
(
γ
)
≠
0
{\displaystyle f(\gamma )\neq 0}
D
<
0
{\displaystyle D<0}
일반적인 3차 방정식의 대수적 해법은 카르다노의 방법 혹은 카르다노의 공식으로 알려져있다
x
3
+
a
x
2
+
b
x
+
c
=
0
{\displaystyle x^{3}+ax^{2}+bx+c=0}
2차항을 없애기 위해, 치환
x
=
t
−
a
/
3
{\displaystyle x=t-a/3}
새로운 방정식
t
3
+
p
t
+
q
=
0
{\displaystyle t^{3}+pt+q=0}
여기서
p
=
b
−
a
2
3
q
=
c
+
2
a
3
−
9
a
b
27
{\displaystyle p=b-{\frac {a^{2}}{3}}\ \ q=c+{\frac {2a^{3}-9ab}{27}}}
x
3
−
3
x
+
1
{\displaystyle x^{3}-3x+1}
편집
3차 방정식의 근의 공식
방정식
x
3
−
3
x
+
1
=
0
{\displaystyle x^{3}-3x+1=0}
p
=
−
3
,
q
=
1
{\displaystyle p=-3,q=1}
−
q
2
+
q
2
4
+
p
3
27
=
−
1
2
+
i
3
2
=
e
2
π
i
/
3
{\displaystyle -{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}=-{\frac {1}{2}}+{\frac {i{\sqrt {3}}}{2}}=e^{2\pi i/3}}
−
q
2
−
q
2
4
+
p
3
27
=
−
1
2
−
i
3
2
=
e
−
2
π
i
/
3
{\displaystyle -{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}=-{\frac {1}{2}}-{\frac {i{\sqrt {3}}}{2}}=e^{-2\pi i/3}}
A
=
e
2
π
i
/
9
{\displaystyle A=e^{2\pi i/9}}
B
=
e
−
2
π
i
/
9
{\displaystyle B=e^{-2\pi i/9}}
ω
=
e
2
π
i
/
3
{\displaystyle \omega =e^{2\pi i/3}}
방정식의 세 근은
A
+
B
,
ω
A
+
ω
2
B
,
ω
2
A
+
ω
B
{\displaystyle A+B,\omega A+\omega ^{2}B,\omega ^{2}A+\omega B}
2
cos
(
2
π
9
)
,
−
2
cos
(
π
9
)
,
2
sin
(
π
18
)
{\displaystyle 2\cos \left({\frac {2\pi }{9}}\right),-2\cos \left({\frac {\pi }{9}}\right),2\sin \left({\frac {\pi }{18}}\right)}
가 된다. 사차 방정식 이란, 최고차항의 차수가 4인 다항 방정식 을 뜻한다. 일반적인 모양은
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
=
0
,
a
≠
0
{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,a\neq 0}
와 같다.
여기에서
a
,
b
,
c
,
d
{\displaystyle a,b,c,d}
x
4
,
x
3
,
x
2
,
x
{\displaystyle x^{4},x^{3},x^{2},x}
계수 라고 한다.
e
{\displaystyle e}
상수항 이라고 부른다.
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
=
0
{\displaystyle \textstyle ax^{4}+bx^{3}+cx^{2}+dx+e=0\ }
이 방정식에서 양변을
x
{\displaystyle x}
a
{\displaystyle a}
x
=
y
−
b
4
a
{\displaystyle \textstyle x=y-{b \over 4a}}
y
4
+
p
y
2
+
q
y
+
r
=
0
{\displaystyle y^{4}+p{y^{2}}+qy+r=0}
y
4
=
−
p
y
2
−
q
y
−
r
{\displaystyle y^{4}=-p{y}^{2}-qy-r}
z
{\displaystyle z}
2
z
y
2
+
z
2
{\displaystyle 2zy^{2}+z^{2}}
(
y
2
+
z
)
2
=
(
2
z
−
p
)
y
2
−
q
y
+
z
2
−
r
{\displaystyle (y^{2}+z)^{2}=(2z-p){y}^{2}-qy+z^{2}-r}
이 된다. 이 우변이 완전제곱식이 되면, 사차방정식은 두 개의 이차방정식 으로 분해된다. 그러므로 우변의 이차식은 판별식
Δ
=
q
2
−
4
(
2
z
−
p
)
(
z
2
−
r
)
{\displaystyle \Delta =q^{2}-4(2z-p)(z^{2}-r)}
의 값이 0이 되어야 한다. 이것은
z
{\displaystyle z}
삼차방정식 이므로 이것을 풀어
z
{\displaystyle z}
(
y
2
+
z
)
2
=
(
s
y
+
t
)
2
{\displaystyle (y^{2}+z)^{2}=(sy+t)^{2}}
의 형태가 된다. 따라서 두 이차방정식
y
2
+
z
=
±
(
s
y
+
t
)
{\displaystyle y^{2}+z=\pm (sy+t)}
기하학 (geometry)은 공간 에 있는 도형이나 대상들의 치수 , 모양 , 상대적 위치 등을 연구하는 수학 의 한 분야이다. 기하학이 다루는 대상으로는 점 , 선 , 면 , 도형, 공간과 같은 것이 있다.[ 1] 영어 단어 "geometry"는 땅을 뜻하는 그리스어 단어 γε(게)와 측정하다를 뜻하는 그리스어 단어 μετρία(메트리아)를 합하여 만든 말로서 고대 그리스 에서부터 사용되었다.
이 부분의 본문은
좌표계 입니다.
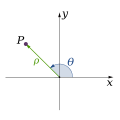
2차원의 좌표는 직교 좌표계 , 극좌표계 , 지리 좌표계 등으로 나타낸다. 2차원의 직교 좌표계를 좌표평면이라고도 한다.
2차원 직교 좌표계 에서
(
a
,
b
)
=
(
1.2
,
−
0.5
)
{\displaystyle (a,b)=(1.2,-0.5)}
r
{\displaystyle r}
2차원 직교 좌표계 에서 원의 중심이
(
a
,
b
)
{\displaystyle (a\,,b\,)}
r
{\displaystyle r\,}
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r\,^{2}}
원의 방정식 이라고 부른다.이는 원의 중심에서 원주상의 임의의 한 점 까지의 거리가 항상 같음을 이용해 서로 다른 두 점 사이의 거리 공식 으로 유도한 것이다.
원을 호도각 에 따른 매개변수 t로 다음과 같이 나타낼 수 있다.
x
=
a
+
r
cos
t
{\displaystyle x=a+r\,\cos t}
y
=
b
+
r
sin
t
{\displaystyle y=b+r\,\sin t}
(
0
≤
t
<
2
π
)
{\displaystyle (0\leq t<2\pi )}
원주상의 한 점
(
x
1
,
y
1
)
{\displaystyle (x\,_{1},y\,_{1})}
접선의 방정식
(
x
1
−
a
)
(
x
−
a
)
+
(
y
1
−
b
)
(
y
−
b
)
=
r
2
{\displaystyle (x\,_{1}-a)(x\,-a)+(y\,_{1}-b)(y\,-b)=r\,^{2}}
기울기가
m
{\displaystyle m\,}
접선의 방정식
y
−
b
=
m
(
x
−
a
)
±
r
2
(
m
2
+
1
)
{\displaystyle y\,-b=m\,(x\,-a)\pm {\sqrt {r\,^{2}(m\,^{2}+1)}}}
수학 에서 집합 (set )은 어떤 조건이 주어졌을때, 그 조건이 가리키는 대상이 분명한 것들의 모임을 말한다. 집합을 다루는 이론을 집합론 이라고 한다.
집합을 이루는 대상 하나하나를 그 집합의 원소 또는 원이라고 한다. 또 어떤 것이 집합의 원소일 때 그것은 그 집합에 속한다라고 한다.
집합 A가 A = {1, 2, 3, 4}라고 할 때 3이 집합 A에 속한다는 것을 다음과 같이 표기한다.
3
∈
A
{\displaystyle 3\in A}
마찬가지로, 5가 집합 A에 속하지 않는다는 것은 다음과 같이 표기한다.
5
∉
A
{\displaystyle 5\notin A}
집합이 가진 원소의 수를 집합의 기수(혹은 크기)라고 한다.
유한 집합 : 집합 {1, 2, 3, 4, 5}의 기수는 5이다. 이와 같이 기수가 유한한 집합공집합 : 기수가 0인 집합, Ø라는 기호로 나타낸다. 예를 들어, '평면 위에서 변이 4개인 삼각형 의 집합'이나 '이차부등식
x
2
+
3
x
+
5
<
0
{\displaystyle x^{2}+3x+5<0}
집합 중에는 자연수의 집합 을 비롯해 무한 히 많은 원소를 가진 것도 있으며, 이를 무한 집합 이라 한다.
집합 A의 모든 원소가 다른 집합 B의 원소가 될 때 'A는 B에 포함된다', 또는 'B는 A를 포함한다'라고 한다. 여기서 A는 B의 부분집합 이다. 또한 자신과 동일하지 않은 자신의 모든 부분집합을 진부분집합이라고 한다. 공집합은 모든 집합의 부분집합이며, 모든 집합은 그 자신의 부분집합이다.
집합간의 포함관계는 다음과 같이 포함(Contain)의 약자 C를 기호화하여 표기한다.
A
⊂
B
{\displaystyle A\subset B}
예를 들어, 두 집합 A, B가 있을 때 A={1,2,3}, B={1,2,3,5,7}이면, A는 B에 포함되고, B는 A를 포함한다.
A의 진부분집합은 Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}의 7개이다. 두 집합 A, B가 가지고 있는 모든 원소가 서로 같다면, 두 집합은 같다(상동)고 말한다. 좀 더 엄밀히 말하면, A가 B의 부분집합이면서 동시에 B가 A의 부분집합이면, 두 집합은 같은 집합이다.
A
=
B
⇔
A
⊂
B
{\displaystyle A=B\Leftrightarrow A\subset B}
B
⊂
A
{\displaystyle B\subset A}
집합 A와 B 벤 다이어그램 (Venn diagram)은 서로 다른 집합 들 사이의 관계를 보여주기 위한 그림이다.
원을 그리고 밖에 집합의 기호를 쓰고 안에 원소를 쓰는 방법이다.
교집합 : 주황색 원(집합 A )은 두 다리를 가진 모든 생물 들의 모임이라고 하고, 푸른 원(집합 B )은 날아다니는 모든 생물들의 모임이라고 하자. 이때 주황색과 푸른색 원이 겹쳐지는 부분은 두 다리를 가지고, 또한 날아다닐 수 있는, 예를 들면 비둘기 같은 생물들의 모임을 나타낸다.
합집합 : A 와 B 의 두 영역을 합친 영역은 A 와 B 의 합집합이다.
집합 A와 B의 교집합
집합 A와 B의 합집합
여집합
B
−
A
{\displaystyle B-A}
교집합 : 두 집합 A와 B가 있을 때, A와 B에 모두 속하는 원소의 집합을 A와 B의 교집합이라 정의하고 A ∩ B 로 적는다. 논리학에서는 A∧B나 A·B로도 표시한다.합집합 : 두 집합 A와 B가 있을 때, A에 속하거나 B에 속하는 원소의 집합을 A와 B의 합집합 (合集合)이라 정의하고
A
∪
B
{\displaystyle A\cup B}
n
(
A
∪
B
)
=
n
(
A
)
+
n
(
B
)
−
n
(
A
∩
B
)
{\displaystyle n(A\cup B)=n(A)+n(B)-n(A\cap B)}
여집합 (차집합) : 차집합 은 집합 에 포함되면서 다른 집합에 포함되지 않는 원소들의 집합으로, 즉 어떤 집합의 원소에서 다른 집합의 원소를 뺀 집합으로 생각할 수 있다. 예를 들어
{
1
,
2
,
3
}
∖
{
2
,
3
,
4
}
=
{
1
}
{\displaystyle \{1,2,3\}\setminus \{2,3,4\}=\{1\}}
실수 의 집합
R
{\displaystyle \mathbb {R} }
유리수 의 집합
Q
{\displaystyle \mathbb {Q} }
무리수 의 집합이 된다. 집합 A의 여집합은 전체집합 U에 대해서
U
∖
A
{\displaystyle U\setminus A}
다음의 집합들은 수학에서 매우 자주 사용되며, 따라서 특별한 기호를 배정해 나타낸다.
N
{\displaystyle \mathbb {N} }
자연수 의 집합이다.
Z
{\displaystyle \mathbb {Z} }
정수 의 집합이다.
Q
{\displaystyle \mathbb {Q} }
유리수 의 집합이다.
I
{\displaystyle \mathbb {I} }
무리수 의 집합이다. 간혹
P
{\displaystyle \mathbb {P} }
R
{\displaystyle \mathbb {R} }
실수 의 집합이다.
C
{\displaystyle \mathbb {C} }
복소수 의 집합이다.실수의 무한수열 수열 (數列, sequence of numbers)은 차례로 수를 나열한 것을 의미한다.[ 2]
수열을 이루는 각각의 수를 수열의 항 또는 원소 , 열 이라고 한다. 수열의 항을 앞에서부터 차례로 나열할 때 앞에서부터 n번째에 오는 항을 제n항이라고 하며, 이를 기호로
a
n
{\displaystyle a_{n}}
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
.
.
.
{\displaystyle a_{1},a_{2},a_{3},a_{4},a_{5},...}
a
1
{\displaystyle a_{1}}
수열에서 제n항
a
n
{\displaystyle a_{n}}
f
(
n
)
{\displaystyle f(n)}
일반항 이라고 한다. n에 대입하는 자연수의 값에 따라 구해지는 모든 항의 값을 일반적으로 나타낸 것이기 때문이다. 다시 말해 일반항
a
n
{\displaystyle a_{n}}
집합 의 조건제시법과 유사하게, {
a
n
{\displaystyle a_{n}}
수열의 일반항이
a
n
=
f
(
n
)
{\displaystyle a_{n}=f(n)}
함수 와 관련지을 때, 정의역 이 자연수 의 집합이고 공역 이 실수 의 집합인 함수 f에 대하여, 자연수 n의 값과 이에 따른 함숫값
f
(
n
)
{\displaystyle f(n)}
n
=
1
,
2
,
3
,
4
,
.
.
.
{\displaystyle n=1,2,3,4,...}
f
(
1
)
,
f
(
2
)
,
f
(
3
)
,
f
(
4
)
,
.
.
.
{\displaystyle f(1),f(2),f(3),f(4),...}
f
(
n
)
=
a
n
{\displaystyle f(n)=a_{n}}
a
1
,
a
2
,
a
3
,
a
4
,
.
.
.
{\displaystyle a_{1},a_{2},a_{3},a_{4},...}
a
n
{\displaystyle a_{n}}
f
(
n
)
{\displaystyle f(n)}
a
n
{\displaystyle a_{n}}
한 수열에서 항의 수를 수열의 길이 라고 하며, 이는 유한 할 수도 있고 무한 할 수도 있다. 항의 수가 유한한 수열을 유한수열, 항의 수가 무한한 수열을 무한수열이라고 한다. 유한수열에서는 항을 차례로 나열할 때 맨 마지막 항이 존재하는데, 이 항을 끝항이라고 한다.
수열의 각 항은 순서에 따라 구분되므로 (1, 2, 3)과 (1, 3, 2)는 엄연히 서로 다른 수열이며, 집합의 경우와 달리 (1, 1, 2)처럼 하나의 수가 두 항에 동시에 등장할 수도 있다.
2, 4, 6, 8, 10, 12, ... : 각 항 간의 차가 일정한 등차수열 이다.
3, 9, 27, 81, 243, ... : 각 항 간의 비가 일정한 등비수열 이다.
1, 4, 10, 19, 31, ... : 계차수열 이 등차수열인 수열이다.
5, 9, 25, 89, 345, ... : 계차수열 이 등비수열인 수열이다.
1, 1, 2, 3, 5, 8, 13, ... : 피보나치 수열 이다.
7, 9, 3, 1, 7, 9, 3, ... :
a
n
=
(
7
n
{\displaystyle a_{n}=(7^{n}}
3, 7, 6, 5, -1, ... : 규칙이 전혀 없는 수열이다.
1, 3, 6, 10, 15, 21, 28, ... : 삼각수 수열이다.
1, 4, 9, 16, 25, 49, 64, ... : 사각수 수열이다.
0, 0, 0, 0, 120, 720, 2520, ... :
a
n
=
n
(
n
−
1
)
(
n
−
2
)
(
n
−
3
)
(
n
−
4
)
{\displaystyle a_{n}=n(n-1)(n-2)(n-3)(n-4)}
수열 {
a
n
{\displaystyle a_{n}}
a
1
+
a
2
+
a
3
+
.
.
.
+
a
n
{\displaystyle a_{1}+a_{2}+a_{3}+...+a_{n}}
∑
{\displaystyle \sum _{}}
∑
k
=
1
n
a
k
{\displaystyle \sum _{k=1}^{n}a_{k}}
여기서,
∑
k
=
1
n
a
k
{\displaystyle \sum _{k=1}^{n}a_{k}}
a
k
{\displaystyle a_{k}}
∑
{\displaystyle \sum _{}}
편집
시그마
∑
{\displaystyle \sum _{}}
∑
k
=
1
n
(
a
k
+
b
k
)
{\displaystyle \sum _{k=1}^{n}(a_{k}+b_{k})}
∑
k
=
1
n
a
k
+
∑
k
=
1
n
b
k
{\displaystyle \sum _{k=1}^{n}a_{k}+\sum _{k=1}^{n}b_{k}}
∑
k
=
1
n
(
a
k
−
b
k
)
{\displaystyle \sum _{k=1}^{n}(a_{k}-b_{k})}
∑
k
=
1
n
a
k
−
∑
k
=
1
n
b
k
{\displaystyle \sum _{k=1}^{n}a_{k}-\sum _{k=1}^{n}b_{k}}
∑
k
=
1
n
c
a
k
{\displaystyle \sum _{k=1}^{n}ca_{k}}
c
{\displaystyle c}
∑
k
=
1
n
a
k
{\displaystyle \sum _{k=1}^{n}a_{k}}
∑
k
=
1
n
c
{\displaystyle \sum _{k=1}^{n}c}
n
c
{\displaystyle nc}
∑
k
=
m
n
a
k
{\displaystyle \sum _{k=m}^{n}a_{k}}
∑
k
=
1
n
a
k
−
∑
k
=
1
m
−
1
a
k
{\displaystyle \sum _{k=1}^{n}a_{k}-\sum _{k=1}^{m-1}a_{k}}
(
m
<
n
)
{\displaystyle (m<n)}
한편, 수열의 일반항이
a
k
=
1
f
(
k
)
g
(
k
)
{\displaystyle a_{k}={\frac {1}{f(k)g(k)}}}
이항분리
1
F
G
=
(
1
G
−
F
)
(
1
F
−
1
G
)
{\displaystyle {\frac {1}{FG}}=({\frac {1}{G-F}})({\frac {1}{F}}-{\frac {1}{G}})}
자연수의 거듭제곱의 합은 다음과 같이 공식화할 수 있다. 이들도 수열의 합을 구하는 데 자주 쓰인다.
1
+
2
+
3
+
.
.
.
+
n
=
∑
k
=
1
n
k
{\displaystyle 1+2+3+...+n=\sum _{k=1}^{n}k}
n
(
n
+
1
)
2
{\displaystyle {\frac {n(n+1)}{2}}}
1
2
+
2
2
+
3
2
+
.
.
.
+
n
2
=
∑
k
=
1
n
k
2
{\displaystyle 1^{2}+2^{2}+3^{2}+...+n^{2}=\sum _{k=1}^{n}k^{2}}
n
(
n
+
1
)
(
2
n
+
1
)
6
{\displaystyle {\frac {n(n+1)(2n+1)}{6}}}
1
3
+
2
3
+
3
3
+
.
.
.
+
n
3
=
∑
k
=
1
n
k
3
{\displaystyle 1^{3}+2^{3}+3^{3}+...+n^{3}=\sum _{k=1}^{n}k^{3}}
(
n
(
n
+
1
)
2
)
2
{\displaystyle ({\frac {n(n+1)}{2}})^{2}}
수학 에서, 등차수열 (等差數列, arithmetic sequence)은 연속하는 두 항의 차이가 모두 일정한 수열 을 뜻한다. 예를 들어 1, 3, 5, 7, 9, ...은 등차수열이다. 이때 두 항의 차이는 이 수열의 모든 연속하는 두 항들에 대해서 공 통적으로 나타나는 차 이므로, 공차 (common difference)라고 한다. 예를 들어, 앞의 수열의 공차는 2이다.
수열의 첫항을
a
1
{\displaystyle a_{1}}
d
{\displaystyle d}
a
n
=
a
1
+
(
n
−
1
)
d
{\displaystyle a_{n}=a_{1}+(n-1)d}
등차수열에서 연속하는 두 수의 차이를 공차(公差)라고 한다. 보통
d
{\displaystyle d}
예시를 들면 다음과 같다.
1, 2, 3, 4,…으로 증가하는 수열이 있을 때, 공차
d
{\displaystyle d}
2, 10, 18, 26, …으로 증가하는 수열이 있을 때, 공차
d
{\displaystyle d}
1, 1, 1, 1, 1, … 이런 수열이 있을 때, 공차
d
{\displaystyle d}
상수수열 이라고 한다)
342, 345, 348,351 …으로 증가하는 수열이 있을 때, 공차
d
{\displaystyle d}
23461234, 23843963, 24226692, 24609421, …으로 증가하는 수열이 있을 때 공차
d
{\displaystyle d}
0, -1, -2, -3, -4 …으로 증가하는 수열이 있을 때, 공차
d
{\displaystyle d}
세 수
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
b
{\displaystyle b}
a
{\displaystyle a}
c
{\displaystyle c}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
b
{\displaystyle b}
a
{\displaystyle a}
c
{\displaystyle c}
b
−
a
=
c
−
b
{\displaystyle b-a=c-b}
b
=
a
+
c
2
{\displaystyle b={\frac {a+c}{2}}}
등차중항은 두 수를 1:1로 내분하는 등분점이라고 생각하면 쉽다. 세 수
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
b
{\displaystyle b}
a
{\displaystyle a}
c
{\displaystyle c}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
d
{\displaystyle d}
b
{\displaystyle b}
a
{\displaystyle a}
d
{\displaystyle d}
c
{\displaystyle c}
a
{\displaystyle a}
d
{\displaystyle d}
b
{\displaystyle b}
c
{\displaystyle c}
수열의 정의상 함수처럼 생각하면 이를 내분점, 혹은 외분점의 의미로 받아 들일 수 있다. 항의 비로 표현이 가능하다. [ 3]
등차급수 (arithmetic series)는 등차수열의 합이다. 초항부터 n번째 항까지의 합
S
n
{\displaystyle S_{n}}
S
n
=
n
(
a
1
+
a
n
)
2
=
n
[
2
a
1
+
(
n
−
1
)
d
]
2
{\displaystyle S_{n}={\frac {n(a_{1}+a_{n})}{2}}={\frac {n[2a_{1}+(n-1)d]}{2}}}
이것은 다음과 같은 방법으로 증명할 수 있다.
S
n
=
a
1
+
a
2
+
⋯
+
a
n
−
1
+
a
n
{\displaystyle S_{n}=a_{1}+a_{2}+\dots +a_{n-1}+a_{n}}
S
n
=
a
n
+
a
n
−
1
+
⋯
+
a
2
+
a
1
{\displaystyle S_{n}=a_{n}+a_{n-1}+\dots +a_{2}+a_{1}}
2
S
n
=
(
a
1
+
a
n
)
+
(
a
2
+
a
n
−
1
)
+
⋯
+
(
a
n
−
1
+
a
2
)
+
(
a
n
+
a
1
)
{\displaystyle 2S_{n}=(a_{1}+a_{n})+(a_{2}+a_{n-1})+\dots +(a_{n-1}+a_{2})+(a_{n}+a_{1})}
2
S
n
=
[
2
a
1
+
(
n
−
1
)
d
]
+
[
2
a
1
+
(
n
−
1
)
d
]
+
⋯
+
[
2
a
1
+
(
n
−
1
)
d
]
+
[
2
a
1
+
(
n
−
1
)
d
]
{\displaystyle 2S_{n}=[2a_{1}+(n-1)d]+[2a_{1}+(n-1)d]+\dots +[2a_{1}+(n-1)d]+[2a_{1}+(n-1)d]}
2
S
n
=
n
[
2
a
1
+
(
n
−
1
)
d
]
{\displaystyle 2S_{n}=n[2a_{1}+(n-1)d]}
S
n
=
n
[
2
a
1
+
(
n
−
1
)
d
]
2
{\displaystyle S_{n}={\frac {n[2a_{1}+(n-1)d]}{2}}}
결론적으로 등차급수는 {
a
n
{\displaystyle a_{n}}
a
n
{\displaystyle a_{n}}
로 정리 할 수 있다.(단, {
a
n
{\displaystyle a_{n}}
등차급수의 공식은 실생활에서는 도형의 넓이(ex-사다리꼴의 넓이)를 구하는데 주로 사용된다.
등차수열의 항과 공차 이용
i
{\displaystyle i}
a
i
{\displaystyle a_{i}}
d
{\displaystyle d}
a
n
=
a
i
+
(
n
−
i
)
d
{\displaystyle a_{n}=a_{i}+(n-i)d}
물론 여기에
i
=
1
{\displaystyle i=1}
a
n
=
a
1
+
(
n
−
1
)
d
{\displaystyle a_{n}=a_{1}+(n-1)d}
이를테면 제5번째 항이 9이고, 공차가 2라면
a
n
=
a
5
+
(
n
−
5
)
d
{\displaystyle a_{n}=a_{5}+(n-5)d}
a
n
=
9
+
2
(
n
−
5
)
{\displaystyle a_{n}=9+2(n-5)}
a
n
=
2
n
−
1
{\displaystyle a_{n}=2n-1}
등비수열 (等比數列, geometric sequence) 또는 기하수열 (幾何數列)은 각 항이 그 앞 항과. 일정한 비를 가지는 수열 을 말한다. 그리고, 이 일정한 비를 공비 (共比, common ratio)라고 한다.
첫항이 a이고 공비가 r인 등비수열은 다음과 같다.
a
,
a
r
,
a
r
2
,
a
r
3
,
⋯
{\displaystyle a,ar,ar^{2},ar^{3},\cdots }
첫항이 a이며, 공비가 r인 등비수열의 n번째 항은 다음과 같다.
a
n
=
a
r
n
−
1
{\displaystyle a_{n}=ar^{n-1}\;}
등비수열은 n ≥ 1에 대해다음과 같은 점화식으로 표현될 수 있다.
a
n
=
r
a
n
−
1
{\displaystyle a_{n}=r\,a_{n-1}}
이를 이용해, 일반적으로 어떤 수열이 등비수열인지 확인하기 위해서는 각각의 연속된 항의 비가 일정한지만 확인하면 된다.
등비수열은 공비에 따라 여러 경향을 보이는데 만약 공비가
양수이면, 모든 항은 첫항과 같은 부호를 가진다.
음수이면, 계속 부호가 번갈아 가며 나타난다.
1보다 크면, 양의 무한대를 향해 지수적으로 증가한다.
1이면, 모든 항의 값이 같아진다.
−1과 1사이에 있지만 0이 아니면, 0을 향해 지수적으로 감소한다.
−1이면, 모든 항의 절댓값 은 같지만, 부호가 계속 번갈아 가며 나타난다.
−1보다 작으면, 음의 무한대를 향해 지수적으로 증가한다. 등비수열은(공비가 −1, 1, 0이 아닌경우) 등차수열 과 같이 선형 변화 를 보이는 것과 달리, 지수적 변화 를 보인다. 이 두 수열은 관계가 전혀 없어 보이지만, 등차수열에 거듭제곱 을 취하면 등비수열이 되고 반대로 등비수열의 각 항에 로그 를 취하면 등차수열이 되는 관계를 가지고 있다.
0이 아닌 세 수
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
b
{\displaystyle b}
a
{\displaystyle a}
c
{\displaystyle c}
등비중항 이라 한다.
따라서 세 수
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
b
{\displaystyle b}
a
{\displaystyle a}
c
{\displaystyle c}
b
a
=
c
b
{\displaystyle {\frac {b}{a}}={\frac {c}{b}}}
b
2
=
a
c
{\displaystyle b^{2}=ac}
또
b
2
=
a
c
{\displaystyle b^{2}=ac}
b
=
±
a
c
{\displaystyle b=\pm {\sqrt {ac}}}
초항부터
n
{\displaystyle n}
a
(
1
−
r
n
)
1
−
r
{\displaystyle {\frac {a(1-r^{n})}{1-r}}}
a
(
r
n
−
1
)
r
−
1
{\displaystyle {\frac {a(r^{n}-1)}{r-1}}}
단,
r
=
1
{\displaystyle r=1}
n
a
{\displaystyle na}
a
1
{\displaystyle a_{1}}
a
n
{\displaystyle a_{n}}
등비급수 (문화어 :영어 : geometric series ) 또는 기하급수
S
n
{\displaystyle S_{n}}
S
n
=
a
+
a
r
1
+
a
r
2
+
a
r
3
+
⋯
+
a
r
n
−
1
{\displaystyle S_{n}=a+ar^{1}+ar^{2}+ar^{3}+\cdots +ar^{n-1}}
=
a
(
1
+
r
1
+
r
2
+
⋯
+
r
n
−
1
)
{\displaystyle =a(1+r^{1}+r^{2}+\cdots +r^{n-1})}
여기에서
r
{\displaystyle r}
S
n
=
a
(
1
+
r
1
+
r
2
+
⋯
+
r
n
−
1
)
(
r
−
1
)
r
−
1
{\displaystyle S_{n}=a{\frac {(1+r^{1}+r^{2}+\cdots +r^{n-1})(r-1)}{r-1}}}
=
a
r
n
−
1
r
−
1
=
a
1
−
r
n
1
−
r
{\displaystyle =a{\frac {r^{n}-1}{r-1}}=a{\frac {1-r^{n}}{1-r}}}
무한등비급수 는 등비수열의 각 항을 무한히 더한 것이며, 그 합은 다음과 같다.
∑
k
=
0
∞
a
r
k
=
lim
n
→
∞
∑
k
=
0
n
−
1
a
r
k
=
lim
n
→
∞
a
(
1
−
r
n
)
1
−
r
=
a
1
−
r
(
{\displaystyle \sum _{k=0}^{\infty }ar^{k}=\lim _{n\to \infty }{\sum _{k=0}^{n-1}ar^{k}}=\lim _{n\to \infty }{\frac {a(1-r^{n})}{1-r}}={\frac {a}{1-r}}(}
|
r
|
<
1
{\displaystyle |r|<1}
자연수
n
{\displaystyle n}
a
n
{\displaystyle a^{n}}
a
n
=
a
×
⋯
×
a
⏟
n
{\displaystyle {{a^{n}=} \atop {\ }}{{\underbrace {a\times \cdots \times a} } \atop n}}
이것은 곱셈 연산이 덧셈 을 반복하는 것과 유사하다. 또한 정의에 따라, 다음의 식이 성립한다.
a
1
=
a
.
{\displaystyle a^{1}=a.}
a
b
a
c
=
a
b
+
c
.
{\displaystyle {a^{b}}{a^{c}}=a^{b+c}.}
(
a
n
)
m
=
a
n
m
.
{\displaystyle (a^{n})^{m}=a^{nm}.}
(
a
b
)
c
=
(
a
c
)
b
{\displaystyle (a^{b})^{c}=(a^{c})^{b}}
a
c
b
c
=
(
a
b
)
c
.
{\displaystyle {a^{c}}{b^{c}}=(ab)^{c}.}
a
m
÷
a
n
=
a
m
−
n
{\displaystyle a^{m}\div a^{n}=a^{m-n}}
a
1
=
a
.
{\displaystyle a^{1}=a.}
a
n
+
1
=
a
×
a
n
,
n
=
1
,
2
,
3
,
⋯
.
{\displaystyle a^{n+1}=a\times a^{n},\ n=1,2,3,\cdots .}
거듭제곱근 거듭제곱근 이란,
a
,
a
3
,
a
4
,
.
.
.
,
a
n
.
.
.
{\displaystyle {\sqrt {a}},{\sqrt[{3}]{a}},{\sqrt[{4}]{a}},...,{\sqrt[{n}]{a}}...}
n이 음의 정수인 경우에는 다음과 같이 정의한다.
a
−
n
=
1
a
n
{\displaystyle a^{-n}={\frac {1}{a^{n}}}}
그리고 이 경우에도
a
n
×
a
m
=
a
n
+
m
{\displaystyle a^{n}\times a^{m}=a^{n+m}}
a
n
×
a
−
n
=
a
n
+
(
−
n
)
{\displaystyle a^{n}\times a^{-n}=a^{n+(-n)}}
a
0
{\displaystyle a^{0}}
[ 4]
a
0
=
1
{\displaystyle a^{0}=1\,}
유리수
q
{\displaystyle q}
q
=
n
m
{\displaystyle q={\frac {n}{m}}}
(
a
q
)
m
=
(
a
n
m
)
m
=
a
n
{\displaystyle (a^{q})^{m}=\left({a^{\frac {n}{m}}}\right)^{m}=a^{n}}
a
n
m
=
a
n
m
{\displaystyle a^{\frac {n}{m}}={\sqrt[{m}]{a^{n}}}}
실수 x에 대해, e 를 밑으로 하는 거듭제곱은 지수 함수 로 정의된다.
또한, 극한 을 이용하여 정의할 수도 있다.
e
x
=
lim
n
→
+
∞
(
1
+
x
n
)
n
{\displaystyle e^{x}=\lim _{n\rightarrow +\infty }\left(1+{\frac {x}{n}}\right)^{n}}
멱급수 로 표현하면 다음과 같다.
e
x
=
∑
n
=
0
∞
x
n
n
!
=
1
+
x
+
x
2
2
+
x
3
6
+
⋯
+
x
n
n
!
+
⋯
{\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots \,}
일반적인 실수에 대해서는 다음과 같이 정의한다.
a
x
=
e
x
ln
a
{\displaystyle a^{x}=e^{x\ln a}\,}
x가 실수일 때, 허수단위
i
{\displaystyle i}
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x\,}
이 식은 오일러 공식 으로도 부르며, 이 식에 따라
e
i
π
=
−
1
{\displaystyle e^{i\pi }=-1\,}
이에 따라서, 복소수
z
=
a
+
b
i
{\displaystyle z=a+bi}
e
z
{\displaystyle e^{z}}
e
z
=
e
a
+
b
i
=
e
a
e
b
i
=
e
a
(
cos
b
+
i
sin
b
)
{\displaystyle e^{z}=e^{a+bi}=e^{a}e^{bi}=e^{a}(\cos b+i\sin b)\,}
그리고, 복소수 가 지수로 오는 거듭제곱은 다음과 같다.
w
z
=
w
a
+
b
i
=
e
(
a
+
b
i
)
ln
w
{\displaystyle w^{z}=w^{a+bi}=e^{(a+bi)\ln w}\,}
상수 법칙
log
a
1
=
0
,
log
a
a
=
1
{\displaystyle \log _{a}1=0,\log _{a}a=1}
덧셈 법칙
log
a
x
y
=
log
a
x
+
log
a
y
{\displaystyle \log _{a}xy=\log _{a}x+\log _{a}y}
뺄셈 법칙
log
a
x
y
=
log
a
x
−
log
a
y
{\displaystyle \log _{a}{\frac {x}{y}}=\log _{a}x-\log _{a}y}
지수 법칙
log
a
x
b
=
b
log
a
x
{\displaystyle \log _{a}x^{b}=b\log _{a}x}
밑 변환 법칙
log
b
x
=
log
k
x
log
k
b
{\displaystyle \log _{b}x={\frac {\log _{k}x}{\log _{k}b}}}
k
>
0
,
k
≠
1
{\displaystyle k>0,{\mbox{ }}k\neq 1}
역수 법칙
log
b
x
=
1
log
x
b
{\displaystyle \log _{b}x={\frac {1}{\log _{x}b}}}
b
≠
1
{\displaystyle b\neq 1}
이러한 특징을 이용해, 복잡한 곱셈 문제를 단순한 덧셈 문제로 바꾸어 풀 수 있다.
행렬의 특정 성분은 문자에 두 개의 첨자를 붙여서 보통 표시한다. 예를 들어, a2,1 는 행렬 A 의 2행 1열에 위치한 원소를 가리킨다. 수학 에서, 행렬 (行列, matrix )은 수 나 기호, 수식 등을 네모꼴로 배열한 것으로, 괄호로 묶어 표시한다. 행렬의 각 항들은 원소(elements) 또는 성분이라고 한다. 여섯 개의 원소를 가진 행렬을 예로 들면 다음과 같다.
[
1
9
−
13
20
55
−
6
]
.
{\displaystyle {\begin{bmatrix}1&9&-13\\20&55&-6\end{bmatrix}}.}
두 행렬이 같다는 것은 행렬의 크기가 같고, 각각의 서로 대응되는 성분들이 같은것을 말한다. 즉, 두 a ×b 행렬 A , m ×n 행렬 B 에 대해서,
이면 두 행렬이 같다고 하고, A = B 라고 쓴다. 이 관계는
반사관계 : A = A 대칭관계 : A = B 이면 B = A 전이관계 : A = B , B = C 이면 A = C 이 성립하므로 동치관계 이다.
주어진 두 m ×n 행렬 A 와 B 에 대해 덧셈 A +B 는 다음과 같이 각 성분의 합으로 정의한다.
(
A
+
B
)
i
j
=
A
i
j
+
B
i
j
{\displaystyle (\mathbf {A} +\mathbf {B} )_{ij}=\mathbf {A} _{ij}+\mathbf {B} _{ij}\ }
마찬가지로 주어진 두 m ×n 행렬 A 와 B 에 대해 뺄셈 A -B 는 다음과 같이 각 성분의 합으로 정의한다.
(
A
−
B
)
i
j
=
A
i
j
−
B
i
j
{\displaystyle (\mathbf {A} -\mathbf {B} )_{ij}=\mathbf {A} _{ij}-\mathbf {B} _{ij}\ }
예를 들어,
[
1
3
7
1
0
0
1
2
2
]
+
[
0
0
5
7
5
0
2
1
1
]
=
[
1
+
0
3
+
0
7
+
5
1
+
7
0
+
5
0
+
0
1
+
2
2
+
1
2
+
1
]
=
[
1
3
12
8
5
0
3
3
3
]
{\displaystyle {\begin{bmatrix}1&3&7\\1&0&0\\1&2&2\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\\2&1&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0&7+5\\1+7&0+5&0+0\\1+2&2+1&2+1\end{bmatrix}}={\begin{bmatrix}1&3&12\\8&5&0\\3&3&3\end{bmatrix}}}
주어진 m ×n 행렬 A 에 스칼라 k를 곱하는 것 kA 는 다음과 같이 A 의 각 성분에 스칼라 k를 곱하는 것으로 정의한다.
(
k
A
)
i
j
=
k
A
i
j
{\displaystyle (k\mathbf {A} )_{ij}=k\mathbf {A} _{ij}\ }
예를 들어,
2
[
1
8
−
3
4
−
2
5
]
=
[
2
⋅
1
2
⋅
8
2
⋅
−
3
2
⋅
4
2
⋅
−
2
2
⋅
5
]
=
[
2
16
−
6
8
−
4
10
]
{\displaystyle 2{\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot -3\\2\cdot 4&2\cdot -2&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}}
a 와 b 를 스칼라, A , B , C 를 크기가 같은 행렬이라 하자. 이때 다음이 성립한다.
A + B = B + A A + (B + C ) = (A + B ) + C (ab )A = a (b A )
(a + b )A = a A + b A
(a - b )A = a A - b A
a (A + B ) = a A + a B a (A - B ) = a A - a B
행렬 A 와 B 를 곱하여 행렬 AB 를 얻는 것을 나타내는 그림. 행렬 간의 곱은 모든 경우에 대해서 정의되는 것이 아니라 다음과 같은 특수한 경우에만 정의한다. 주어진 m ×k 행렬 A , k ×n 행렬 B 의 곱은 m ×n 행렬이 되고 각 성분은 다음과 같이 A의 행벡터와 B의 열벡터의 내적 으로 정의한다.
(
A
B
)
i
j
=
∑
l
=
1
k
A
i
l
B
l
j
{\displaystyle (\mathbf {AB} )_{ij}=\sum _{l=1}^{k}\mathbf {A} _{il}\mathbf {B} _{lj}}
예를 들어,
[
1
0
2
−
1
3
1
]
⋅
[
3
1
2
1
1
0
]
=
[
(
1
⋅
3
+
0
⋅
2
+
2
⋅
1
)
(
1
⋅
1
+
0
⋅
1
+
2
⋅
0
)
(
−
1
⋅
3
+
3
⋅
2
+
1
⋅
1
)
(
−
1
⋅
1
+
3
⋅
1
+
1
⋅
0
)
]
=
[
5
1
4
2
]
{\displaystyle {\begin{bmatrix}1&0&2\\-1&3&1\\\end{bmatrix}}\cdot {\begin{bmatrix}3&1\\2&1\\1&0\end{bmatrix}}={\begin{bmatrix}(1\cdot 3+0\cdot 2+2\cdot 1)&(1\cdot 1+0\cdot 1+2\cdot 0)\\(-1\cdot 3+3\cdot 2+1\cdot 1)&(-1\cdot 1+3\cdot 1+1\cdot 0)\\\end{bmatrix}}={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}}
a 를 스칼라, A , B , C 를 크기가 같은 행렬이라 하자. 이때 다음이 성립한다.
A (BC ) = (AB )C A (B + C ) = AB + AC (B + C )A = BA + CA
A (B - C ) = AB - AC (B - C )A = BA - CA
a (BC ) = (a B )C = B (a C )
행렬의 곱은 교환법칙 이 성립하지 않는 비가환 곱이다. AB 와 BA 가 모두 정의된다고 해도, 이 두 결과는 일반적으로 같지 않다.
AB ≠ BA 다만, 특수한 조건을 만족하는 경우에는 교환법칙이 성립한다. 다음과 같은 조건을 만족할 때 행과 열의 갯수가 같은 정사각형 모양의 행렬 A 와 B 에 대해 곱셈의 교환법칙이 성립한다.[ 5]
A
+
B
=
A
B
{\displaystyle A+B=AB}
A
B
=
B
A
{\displaystyle AB=BA}
A
B
=
k
E
{\displaystyle AB=kE}
E 는 단위행렬)이면
A
B
=
B
A
{\displaystyle AB=BA}
A
B
=
B
n
{\displaystyle AB=B^{n}}
A
B
=
B
A
{\displaystyle AB=BA}
B
=
p
A
n
+
q
E
{\displaystyle B=pA^{n}+qE}
A
B
=
B
A
{\displaystyle AB=BA}
a
A
+
b
B
=
E
{\displaystyle aA+bB=E}
A
B
=
B
A
{\displaystyle AB=BA}
위의 조건들은 충분조건 이다. 즉, 정사각형 모양의 행렬 A 와 B 가 위의 조건을 만족할 때 곱셈의 교환법칙이 성립하지만, 곱셈의 교환법칙이 성립하는 모든 행렬이 위의 조건을 만족하는 것은 아니다.[ 5]
일반적으로 곱셈의 교환조건을 만족하는 정사각형 모양의 행렬 A 와 B 는 다음의 교환법칙을 만족하고 그 역도 만족한다. 즉 다음의 식에 대해 필요충분조건 을 이룬다.[ 5]
(
A
−
k
E
)
(
B
−
k
E
)
=
(
B
−
k
E
)
(
A
−
k
E
)
{\displaystyle (A-kE)(B-kE)=(B-kE)(A-kE)}
선형대수학 에서 가역행렬 (invertible matrix),정칙행렬 (正則行列,regular matrix) 또는 비특이행렬 (non-singular matrix)은 역행렬 (inverse matrix)을 갖는
n
×
n
{\displaystyle n\times n}
행렬 을 가리킨다.
역행렬이란, 어떤 행렬
A
{\displaystyle A}
B
{\displaystyle B}
A
B
=
B
A
=
I
n
{\displaystyle AB=BA=I_{n}\ }
여기서
I
n
{\displaystyle I_{n}}
n
×
n
{\displaystyle n\times n}
단위행렬 을 말한다.
이런 성질을 만족하는
B
{\displaystyle B}
A
{\displaystyle A}
A
−
1
{\displaystyle A^{-1}}
역행렬을 갖지 않는 행렬을 비가역행렬 , 또는 특이행렬 이라 한다. 대개 실수 나 복소수 위에 정의된 행렬에 대해 역행렬을 정의하지만, 임의의 환 위에 정의된 행렬에 대해서도 마찬가지로 이 정의를 적용할 수 있다.
위의 공통인자 방정식에서
n
{\displaystyle n}
A
−
1
=
[
a
b
c
d
]
−
1
=
1
a
d
−
b
c
[
d
−
b
−
c
a
]
{\displaystyle A^{-1}={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}^{-1}={\frac {1}{ad-bc}}{\begin{bmatrix}d&-b\\-c&a\\\end{bmatrix}}}
2 × 2 행렬의 역행렬은 위 방법을 통해 빠르게 계산할 수 있다.
위의 공통인자 방정식에서
n
{\displaystyle n}
A
−
1
=
[
a
b
c
d
e
f
g
h
i
]
−
1
=
1
|
A
|
[
e
i
−
f
h
c
h
−
b
i
b
f
−
c
e
f
g
−
d
i
a
i
−
c
g
c
d
−
a
f
d
h
−
e
g
b
g
−
a
h
a
e
−
b
d
]
{\displaystyle A^{-1}={\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\\\end{bmatrix}}^{-1}={\frac {1}{|A|}}{\begin{bmatrix}ei-fh&ch-bi&bf-ce\\fg-di&ai-cg&cd-af\\dh-eg&bg-ah&ae-bd\end{bmatrix}}}
|
A
|
=
a
(
e
i
−
f
h
)
−
b
(
d
i
−
f
g
)
+
c
(
d
h
−
e
g
)
{\displaystyle |A|=a(ei-fh)-b(di-fg)+c(dh-eg)\ }
3 × 3 행렬의 역행렬은 위 방법을 통해 빠르게 계산할 수 있다.
비슷한 이름의
삼각형함수 에 관해서는 해당 문서를 참고하십시오.
수학 에서, 삼각함수 (三角函數, 영어 : trigonometric function )는 직각삼각형의 각 을 직각삼각형의 변들의 길이의 비로 나타내는 함수이다. 이는 복소수의 지수 함수 의 실수 · 허수 부분이며, 따라서 복소수 를 다룰 때 핵심적인 역할을 한다. 가장 근본적인 주기함수 이며, 각종 주기적 현상을 다룰 때 푸리에 급수 의 형태로 등장한다.
삼각함수에는 3개의 기본 함수가 있으며, 이들은 사인 (영어 : sine , 기호 sin) · 코사인 ( 영어 : cosine , 기호 cos) · 탄젠트 (영어 : tangent , 기호 tan)라고 한다. 이들의 역수는 각각 코시컨트 (영어 : cosecant , 기호 csc) · 시컨트 (영어 : secant , 기호 sec) · 코탄젠트 (영어 : cotangent , 기호 cot)라고 한다.
y = ex 의 그래프지수 함수 (指數函數, 영어 : exponential function )란 거듭제곱 의 지수 를 변수로 하고, 정의역을 실수 전체로 정의하는 초월함수 이다. 로그 함수 의 역함수 이다.
정의
a
{\displaystyle a}
x
{\displaystyle x}
y
=
a
x
{\displaystyle y=a^{x}}
f
(
x
)
=
2
x
{\displaystyle f(x)=2^{x}}
exp
(
x
)
{\displaystyle {\text{exp}}(x)}
e
x
{\displaystyle e^{x}}
e
{\displaystyle e}
y
=
e
x
{\displaystyle y=e^{x}}
x
{\displaystyle x}
x
{\displaystyle x}
x
{\displaystyle x}
a 가 음이 아닌 실수, x 가 임의의 실수일 때, a 를 밑 , x 를 지수로 하는 지수함수를 a x 자연수 (혹은 유리수 )일 때, 이함수는 a 의 거듭제곱과 일치한다. 지수함수는 다음의 공리에 의해 정의된다.
a x R 에서 (0, ∞) 로의 연속사상 이다.a 0 = 1a p +q a p a q 다양한 로그 곡선. 붉은 색은 밑이 e 로그 (logarithm, log)는 수학 함수 의 일종으로, 어떤 수를 나타내기 위해 고정된 밑 을 몇 번 곱하여야 하는지를 나타내는 함수이다. 이른 17세기에 곱하기 및 나누기의 계산을 간편하게 해내기 위해 존 네이피어 가 발명한 것으로 알려져 있다. 복잡한 단위의 계산을 간편하게 계산 할 수 있다는 장점 때문에, 로그표 및 계산자 등의 발명품과 함께 세계적으로, 여러 분야의 학자들에게 널리 퍼졌다. 지수 에 대비된다는 의미에서 대수 (對數)로 부르기도 한다.
a
>
0
{\displaystyle a>0}
a
≠
1
{\displaystyle a\neq 1}
y
>
0
{\displaystyle y>0}
x
,
y
{\displaystyle x,y}
y
=
a
x
{\displaystyle y=a^{x}}
x
{\displaystyle x}
a
{\displaystyle a}
y
{\displaystyle y}
log
a
y
=
x
{\displaystyle \log _{a}y=x}
예를 들어
3
4
=
81
{\displaystyle 3^{4}=81}
log
3
81
=
4
{\displaystyle \log _{3}81=4}
이 때
a
≠
1
{\displaystyle a\neq 1}
x
{\displaystyle x}
로그 함수는 다음과 같은 특수한 특징을 가지고 있다.
상수 법칙
log
a
1
=
0
,
log
a
a
=
1
{\displaystyle \log _{a}1=0,\log _{a}a=1}
덧셈 법칙
log
a
x
y
=
log
a
x
+
log
a
y
{\displaystyle \log _{a}xy=\log _{a}x+\log _{a}y}
뺄셈 법칙
log
a
x
y
=
log
a
x
−
log
a
y
{\displaystyle \log _{a}{\frac {x}{y}}=\log _{a}x-\log _{a}y}
지수 법칙
log
a
x
b
=
b
log
a
x
{\displaystyle \log _{a}x^{b}=b\log _{a}x}
밑 변환 법칙
log
b
x
=
log
k
x
log
k
b
{\displaystyle \log _{b}x={\frac {\log _{k}x}{\log _{k}b}}}
k
>
0
,
k
≠
1
{\displaystyle k>0,{\mbox{ }}k\neq 1}
역수 법칙
log
b
x
=
1
log
x
b
{\displaystyle \log _{b}x={\frac {1}{\log _{x}b}}}
b
≠
1
{\displaystyle b\neq 1}
이러한 특징을 이용해, 복잡한 곱셈 문제를 단순한 덧셈 문제로 바꾸어 풀 수 있다.
수학 에서 쌍곡선함수 (双曲線函數)는 일반적인 삼각함수 와 유사한 성질을 갖는 함수로 삼각함수가 단위원 그래프를 매개변수 로 표시할 때 나오는 것처럼, 표준쌍곡선 을 매개변수로 표시할 때 나온다.
sinh , cosh , tanh csch , sech , coth 삼각함수 (원함수 )의 사인, 코사인, 탄젠트 등에서 유추되어 각각에 대응되는 다음과 같은 함수가 있다.
sinh
x
=
e
x
−
e
−
x
2
=
−
i
sin
i
x
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}=-i\sin ix\!}
cosh
x
=
e
x
+
e
−
x
2
=
cos
i
x
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}=\cos ix\!}
쌍곡탄젠트(hyperbolic tangent )
tanh
x
=
sinh
x
cosh
x
{\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}}
=
e
x
−
e
−
x
2
e
x
+
e
−
x
2
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
=
−
i
tan
i
x
{\displaystyle ={\frac {\frac {e^{x}-e^{-x}}{2}}{\frac {e^{x}+e^{-x}}{2}}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}=-i\tan ix\!}
쌍곡코탄젠트(hyperbolic cotangent )
coth
x
=
cosh
x
sinh
x
{\displaystyle \coth x={\frac {\cosh x}{\sinh x}}}
=
e
x
+
e
−
x
2
e
x
−
e
−
x
2
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
=
i
cot
i
x
{\displaystyle ={\frac {\frac {e^{x}+e^{-x}}{2}}{\frac {e^{x}-e^{-x}}{2}}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}=i\cot ix\!}
sech
x
=
1
cosh
x
=
2
e
x
+
e
−
x
=
sec
i
x
{\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}=\sec {ix}\!}
쌍곡코시컨트(hyperbolic cosecant )
csch
x
=
1
sinh
x
=
2
e
x
−
e
−
x
=
i
csc
i
x
{\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}=i\,\csc \,ix\!}
y = ex 의 그래프지수 함수 (指數函數, 영어 : exponential function )란 거듭제곱 의 지수 를 변수로 하고, 정의역을 실수 전체로 정의하는 초월함수 이다. 로그 함수 의 역함수 이다.
밑이 e e x e x e x
exp
(
x
)
{\displaystyle \exp(x)}
a x 자연로그 ln 을 사용하여,
e
ln
a
x
=
e
x
ln
a
{\displaystyle e^{\ln a^{x}}=e^{x\ln a}}
a x a )a x a x a 가 된다.
exp
(
x
)
{\displaystyle \exp(x)}
미분방정식
d
y
/
d
x
=
y
{\displaystyle dy/dx=y}
특수해 가 된다. 이는 반대로 미분방정식
d
y
/
d
x
=
y
,
y
(
0
)
=
1
{\displaystyle dy/dx=y,\;y(0)=1}
해석학 에서 지수 함수는 주로 밑이 e
음함수 미분을 이용하여
d
d
x
a
x
{\displaystyle {\frac {d}{dx}}a^{x}}
y
=
a
x
{\displaystyle y=a^{x}}
ln
y
=
ln
a
x
=
x
ln
a
{\displaystyle \ln y=\ln a^{x}=x\ln a}
좌변을
x
{\displaystyle x}
1
y
d
y
d
x
=
ln
a
⇒
d
y
d
x
=
(
ln
a
)
y
=
(
ln
a
)
a
x
{\displaystyle {\frac {1}{y}}{\frac {dy}{dx}}=\ln a\;\Rightarrow {\frac {dy}{dx}}=(\ln a)y=(\ln a)a^{x}}
삼각함수 (trigonometric function)는 직각삼각형의 각 을 직각삼각형의 변들의 길이의 비로 나타내는 함수이다. 이는 복소수의 지수 함수 의 실수 · 허수 부분이며, 따라서 복소수 를 다룰 때 핵심적인 역할을 한다. 가장 근본적인 주기함수 이며, 각종 주기적 현상을 다룰 때 푸리에 급수 의 형태로 등장한다.
A right triangle always includes a 90° (π/2 radians) angle, here labeled C. Angles A and B may vary. Trigonometric functions specify the relationships among side lengths and interior angles of a right triangle. 삼각함수에는 3개의 기본 함수는
기본 함수
역수
함수
기호
삼각비
함수
기호
삼각비
사인 (sine)
sin
sin
A
=
a
h
{\displaystyle \sin A={\frac {a}{h}}}
코시컨트 (cosecant)
csc
csc
A
=
1
sin
A
=
h
a
{\displaystyle \csc A={\frac {1}{\sin A}}={\frac {h}{a}}}
코사인 (cosine)
cos
cos
A
=
b
h
{\displaystyle \cos A={\frac {b}{h}}}
시컨트 (secant)
sec
sec
A
=
1
cos
A
=
h
b
{\displaystyle \sec A={\frac {1}{\cos A}}={\frac {h}{b}}}
탄젠트 (tangent)
tan
tan
A
=
a
b
{\displaystyle \tan A={\frac {a}{b}}}
코탄젠트 (cotangent)
cot
cot
A
=
1
tan
A
=
b
a
{\displaystyle \cot A={\frac {1}{\tan A}}={\frac {b}{a}}}
라고 한다.
Function
Abbreviation
Description
Identities (using radians )
sine
sin
opposite / hypotenuse
sin
θ
=
cos
(
π
2
−
θ
)
=
1
csc
θ
{\displaystyle \sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc \theta }}}
cosine
cos
adjacent / hypotenuse
cos
θ
=
sin
(
π
2
−
θ
)
=
1
sec
θ
{\displaystyle \cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sec \theta }}\,}
tangent
tan (or tg)
opposite / adjacent
tan
θ
=
sin
θ
cos
θ
=
cot
(
π
2
−
θ
)
=
1
cot
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cot \theta }}}
cotangent
cot (or cotan or cotg or ctg or ctn)
adjacent / opposite
cot
θ
=
cos
θ
sin
θ
=
tan
(
π
2
−
θ
)
=
1
tan
θ
{\displaystyle \cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\tan \theta }}}
secant
sec
hypotenuse / adjacent
sec
θ
=
csc
(
π
2
−
θ
)
=
1
cos
θ
{\displaystyle \sec \theta =\csc \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cos \theta }}}
cosecant
csc (or cosec)
hypotenuse / opposite
csc
θ
=
sec
(
π
2
−
θ
)
=
1
sin
θ
{\displaystyle \csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sin \theta }}}
삼각함수와 각운동 삼각함수 그래프 삼각함수 사인법칙 은 임의의 삼각형 ABC에서 각 A , B , C 의 대변 a , b , c 에 대해 다음과 같은 관계를 만족함을 나타낸다.
sin
A
a
=
sin
B
b
=
sin
C
c
{\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}}
마찬가지로,
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R}
도 성립한다. 여기서 R 은 삼각형의 외접원의 반지름의 길이를 나타낸다.
코사인법칙 에는 총 두 가지의 법칙이 있다.
코사인 제 1 법칙 에 따르면,
c
=
b
cos
A
+
a
cos
B
{\displaystyle \,c=b\cos A+a\cos B}
앙변의 길이와 알고자 하는 변 사이의 두 각의 크기를 알 경우, 다른 한 변의 길이를 알아낼 때 사용할 수 있다.
코사인 제 2 법칙 은 피타고라스의 정리 를 확장한 것이다.
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle \,c^{2}=a^{2}+b^{2}-2ab\cos C}
가 성립하고, 위의 식을 변형하면
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
와 같이 나타낼 수 있다.
코사인법칙은 두 변의 길이와 끼인각의 크기를 알 때 삼각형의 나머지 한 변의 길이를 구할 때 유용하게 쓸 수 있다. 또한 모든 변의 길이를 알고 있을 때 각의 코사인값을 구할 때에도 사용할 수 있다.
탄젠트법칙은 임의의 삼각형 ABC에서 각 A , B 의 대변 a , b 에 다음과 같은 식을 만족시킨다.
a
+
b
a
−
b
=
tan
1
2
(
A
+
B
)
tan
1
2
(
A
−
B
)
{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan {{1 \over 2}(A+B)}}{\tan {{1 \over 2}(A-B)}}}}
수열의 극한 (limit of sequences )은 해석학 의 바탕이 되는 중요한 개념 가운데 하나이다. 수열의 극한 개념은 함수의 극한 으로 확장되었으며 이는 해석학의 중요한 도구인 미분 과 적분 의 개념을 정립하는 데 결정적인 역할을 했다.
직관적으로 말해, 수열
{
a
n
}
{\displaystyle \{a_{n}\}\,}
n
{\displaystyle n\,}
a
n
{\displaystyle a_{n}\,}
a
{\displaystyle a\,}
a
{\displaystyle a\,}
수열
{
a
n
}
{\displaystyle \{a_{n}\}\,}
의 극한 이라고 한다. 수열이 수렴하지 않으면 (즉 극한을 갖지 않으면) 발산한다 고 한다.
예를 들어 수열
1
,
1
2
,
1
3
,
1
4
,
…
{\displaystyle \textstyle {1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},\ldots \,}}
0
{\displaystyle 0\,}
0
{\displaystyle 0\,}
0
,
1
,
0
,
1
,
…
{\displaystyle 0,1,0,1,\ldots \,}
수열의 극한은 실수 집합, 넓게는 임의의 거리 공간 과 위상 공간 위에 정의될 수 있다.
수렴하는 수열의 극한은 유일하다.
수렴하는 수열은 유계 이다. 즉, 모든 자연수
n
{\displaystyle n}
|
a
n
|
≤
M
{\displaystyle |a_{n}|\leq M}
M
>
0
{\displaystyle M>0}
수렴 수열
{
x
n
}
{\displaystyle \{x_{n}\}}
{
y
n
}
{\displaystyle \{y_{n}\}}
x
n
≤
y
n
{\displaystyle x_{n}\leq y_{n}}
N
{\displaystyle N}
n
{\displaystyle n}
lim
n
→
∞
x
n
≤
lim
n
→
∞
y
n
{\displaystyle \lim _{n\to \infty }x_{n}\leq \lim _{n\to \infty }y_{n}}
수렴 수열
{
x
n
}
{\displaystyle \{x_{n}\}}
{
y
n
}
{\displaystyle \{y_{n}\}}
lim
n
→
∞
x
n
<
lim
n
→
∞
y
n
{\displaystyle \lim _{n\to \infty }x_{n}<\lim _{n\to \infty }y_{n}}
N
{\displaystyle N}
n
{\displaystyle n}
x
n
<
y
n
{\displaystyle x_{n}<y_{n}}
x
n
≤
y
n
≤
z
n
{\displaystyle x_{n}\leq y_{n}\leq z_{n}}
n
>
N
{\displaystyle n>N}
lim
n
→
∞
x
n
=
lim
n
→
∞
z
n
=
L
{\displaystyle \lim _{n\to \infty }x_{n}=\lim _{n\to \infty }z_{n}=L}
lim
n
→
∞
y
n
=
L
{\displaystyle \lim _{n\to \infty }y_{n}=L}
샌드위치 정리 )단조 이며 유계 인 수열은 수렴한다. (단조 수렴 정리 )두 수열
{
x
n
}
{\displaystyle \{x_{n}\}\,}
{
y
n
}
{\displaystyle \{y_{n}\}\,}
lim
n
→
∞
x
n
=
x
{\displaystyle \lim _{n\to \infty }x_{n}=x}
lim
n
→
∞
y
n
=
y
{\displaystyle \lim _{n\to \infty }y_{n}=y}
일 때, 일반적으로 사칙연산과 극한의 순서는 교환 가능하다. 즉, 다음이 성립한다.
lim
n
→
∞
(
x
n
+
y
n
)
=
x
+
y
{\displaystyle \lim _{n\to \infty }(x_{n}+y_{n})=x+y}
lim
n
→
∞
(
x
n
−
y
n
)
=
x
−
y
{\displaystyle \lim _{n\to \infty }(x_{n}-y_{n})=x-y}
lim
n
→
∞
x
n
y
n
=
x
y
{\displaystyle \lim _{n\to \infty }x_{n}y_{n}=xy}
lim
n
→
∞
x
n
y
n
=
x
y
{\displaystyle \lim _{n\to \infty }{\frac {x_{n}}{y_{n}}}={\frac {x}{y}}}
y
n
≠
0
{\displaystyle y_{n}\neq 0\,}
y
≠
0
{\displaystyle y\neq 0}
또한 아래의 성질도 성립한다.
lim
n
→
∞
(
c
+
x
n
)
=
c
+
x
{\displaystyle \lim _{n\to \infty }(c+x_{n})=c+x}
lim
n
→
∞
c
x
n
=
c
x
{\displaystyle \lim _{n\to \infty }cx_{n}=cx}
lim
n
→
∞
x
n
α
=
x
α
{\displaystyle \lim _{n\to \infty }x_{n}^{\alpha }=x^{\alpha }}
α
∈
R
{\displaystyle \alpha \in \mathbb {R} }
수열
1
,
−
1
,
1
,
−
1
,
1
,
…
{\displaystyle 1,-1,1,-1,1,\ldots \,}
수열
1
,
−
1
2
,
1
3
,
−
1
4
,
…
{\displaystyle 1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},\ldots \,}
다음은 잘 알려진 수렴하는 수열의 예이다.
lim
n
→
∞
c
=
c
{\displaystyle \lim _{n\to \infty }c=c}
c 는 상수
lim
n
→
∞
1
n
p
=
0
,
p
>
0
{\displaystyle \lim _{n\to \infty }{\frac {1}{n^{p}}}=0,\ p>0}
lim
n
→
∞
a
n
=
0
,
|
a
|
<
1
{\displaystyle \lim _{n\to \infty }a^{n}=0,\ |a|<1}
lim
n
→
∞
a
n
=
1
,
a
>
0
{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{a}}=1,\ a>0}
lim
n
→
∞
n
n
=
1
{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=1}
임의의 실수로 수렴하는 수열을 십진법 에 의한 내림 근사를 이용하여 만들 수 있다. 예를 들어 수열
0.3
,
0.33
,
0.333
,
…
{\displaystyle 0.3,0.33,0.333,\ldots }
1
3
{\displaystyle {\frac {1}{3}}}
1.4
,
1.41
,
1.414
,
…
{\displaystyle 1.4,1.41,1.414,\ldots }
2
{\displaystyle {\sqrt {2}}}
코시 수열 이다.
다음 수열의 극한은 직관적이지 않을 수 있다.
수열
(
1
+
1
n
)
n
{\displaystyle (1+{\frac {1}{n}})^{n}}
e
(
1
+
r
n
)
n
{\displaystyle (1+{\frac {r}{n}})^{n}}
e
r
{\displaystyle e^{r}}
산술 기하 평균 은 산술 평균 과 기하 평균 에 의한 점화 수열 의 극한이다.
lim
n
→
∞
n
(
a
1
n
−
1
)
=
ln
a
,
a
>
0
{\displaystyle \lim _{n\to \infty }n(a^{\frac {1}{n}}-1)=\ln {a},\ a>0}
lim
n
→
∞
(
1
+
1
2
+
1
3
+
⋯
+
1
n
−
ln
n
)
=
γ
{\displaystyle \lim _{n\to \infty }(1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}-\ln {n})=\gamma }
오일러-마스케로니 상수 )
x
{\displaystyle x}
함수
f
(
x
)
{\displaystyle f(x)}
정의역 의 원소
x
{\displaystyle x}
a
{\displaystyle a}
f
(
x
)
{\displaystyle f(x)}
c
{\displaystyle c}
f
(
x
)
{\displaystyle f(x)}
x
→
a
{\displaystyle x\,\to \,a}
c
{\displaystyle c}
수렴 한다고 하고
c
{\displaystyle c}
함수의 극한 이라 한다. 이는
x
→
a
{\displaystyle x\,\to \,a}
f
(
x
)
→
c
{\displaystyle f(x)\,\to \,c}
또는 더 간단히
lim
x
→
a
f
(
x
)
=
c
{\displaystyle \lim _{x\to a}f(x)=c}
의 형식으로 나타낼 수 있다.
일변수 함수의 극한은 일반적으로 엡실론-델타(ε-δ)에 관한 방법
모든 양의 실수
ϵ
{\displaystyle \epsilon }
δ
{\displaystyle \delta }
0
<
|
x
−
p
|
<
δ
{\displaystyle 0<|x-p|<\delta }
|
f
(
x
)
−
c
|
<
ϵ
{\displaystyle |f(x)-c|<\epsilon }
lim
x
→
p
f
(
x
)
=
c
{\displaystyle \lim _{x\to p}f(x)=c}
로 정의한다.
좌극한 과 우극한 (영어 : left-handed limit, right-handed limit )도 비슷한 방법으로 정의하는데, 이때는
δ
{\displaystyle \delta }
0
<
|
x
−
p
|
<
δ
{\displaystyle 0<|x-p|<\delta }
0
<
p
−
x
<
δ
{\displaystyle 0<p-x<\delta }
0
<
x
−
p
<
δ
{\displaystyle 0<x-p<\delta }
한쪽극한 (영어 : one-sided limit )이라고 한다.[ 6]
예를 들어 함수
f
(
x
)
{
1
x
≥
0
0
x
<
0
{\displaystyle f(x){\begin{cases}1&x\geq 0\\0&x<0\end{cases}}}
의 좌극한과 우극한은 각각
lim
x
→
0
−
0
f
(
x
)
=
0
{\displaystyle \lim _{x\to 0-0}f(x)=0}
lim
x
→
0
+
0
f
(
x
)
=
1
{\displaystyle \lim _{x\to 0+0}f(x)=1}
0+0, 0-0의 경우 간단히 +0, -0으로 줄여서 표기하기도 한다. 또는 +0, -0을 줄여 +, -로 표기하기도 한다.
lim
x
→
∞
f
(
x
)
=
L
:
x
{\displaystyle \lim _{x\to \infty }f(x)=L\,:\ x}
f
(
x
)
{\displaystyle f(x)\,}
L
{\displaystyle L\,}
x
{\displaystyle x}
ϵ
{\displaystyle \epsilon }
S
{\displaystyle S}
x
>
S
{\displaystyle x>S}
x
<
S
{\displaystyle x<S}
|
f
(
x
)
−
c
|
<
ϵ
{\displaystyle |f(x)-c|<\epsilon }
양의 무한대:
lim
x
→
∞
f
(
x
)
=
c
{\displaystyle \lim _{x\to \infty }f(x)=c}
음의 무한대:
lim
x
→
−
∞
f
(
x
)
=
c
{\displaystyle \lim _{x\to -\infty }f(x)=c}
극한값이 존재하지 않는 경우(수렴하지 않는 경우)를 발산 한다고 한다. 이때 함숫값이 무한히 커지거나 작아지는 경우에는 특별히 양의 무한대로 발산 하거나 음의 무한대로 발산 한다고 정의한다.
예를 들어,
f
(
x
)
=
1
x
2
{\displaystyle f(x)={\frac {1}{x^{2}}}}
x
{\displaystyle x}
0
{\displaystyle 0}
f
(
x
)
{\displaystyle f(x)}
M
{\displaystyle M}
δ
{\displaystyle \delta }
0
<
|
x
−
p
|
<
δ
{\displaystyle 0<|x-p|<\delta }
f
(
x
)
>
M
{\displaystyle f(x)>M}
lim
x
→
p
f
(
x
)
=
+
∞
{\displaystyle \lim _{x\to p}f(x)=+\infty }
로 정의한다. 음의 무한대로 발산할 경우 마찬가지로 모든 음의 실수
N
{\displaystyle N}
δ
{\displaystyle \delta }
0
<
|
x
−
p
|
<
δ
{\displaystyle 0<|x-p|<\delta }
f
(
x
)
<
N
{\displaystyle f(x)<N}
lim
x
→
p
f
(
x
)
=
−
∞
{\displaystyle \lim _{x\to p}f(x)=-\infty }
로 정의한다.
x
=
a
{\displaystyle x=a}
I
a
{\displaystyle I_{a}}
f
:
I
a
⊂
R
→
R
{\displaystyle f:I_{a}\subset \mathbb {R} \to \mathbb {R} }
lim
x
→
a
f
(
x
)
=
b
{\displaystyle \lim _{x\to a}f(x)=b}
x
=
b
{\displaystyle x=b}
I
b
{\displaystyle I_{b}}
g
:
I
b
⊂
R
→
R
{\displaystyle g:I_{b}\subset \mathbb {R} \to \mathbb {R} }
x
=
b
{\displaystyle x=b}
연속 이고
f
{\displaystyle f}
f
(
I
a
)
⊂
I
b
{\displaystyle f(I_{a})\subset I_{b}}
lim
x
→
a
(
g
∘
f
)
(
x
)
=
g
(
lim
x
→
a
f
(
x
)
)
=
g
(
b
)
{\displaystyle \lim _{x\to a}\left(g\circ f\right)\left(x\right)=g(\lim _{x\to a}f(x))=g(b)}
미분 (微分)은 함수 의 순간변화율을 구하는 계산 과정이다.[ 7] 적분 과 함께 미적분학 을 이룬다.
순간변화율은 평균변화율의 극한으로 생각할 수 있다. 우선, 함수
f
(
x
)
{\displaystyle f(x)}
Δ
x
{\displaystyle \Delta x}
[ 주해 1]
f
(
x
)
{\displaystyle f(x)}
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle f(x+\Delta x)-f(x)}
Δ
f
(
x
)
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {\Delta f(x)}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
를 구할 수 있을 때 이를 평균변화율 이라고 한다.[ 7]
평균변화율의 극한 을 취하여 함수 f(x)의 특정 지점 x 에서 변화량 Δ x 가 0으로 수렴할 때의 변화율을 순간변화율 또는 미분계수 라고 하고 다음의 수식과 같이 나타낸다.[ 8]
d
d
x
f
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {d}{dx}}f(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
미분은 연속적이고 지속적인 변화량에 대한 순간변화율을 의미한다. 따라서 연속적이지 않은 변화량에서나 첨점 과 같은 특이점에서는 미분이 불가능하다. 함수의 그래프 에서 미분은 함수 곡선의 특정 지점에서 접선 으로 나타낼 수 있다.
함수
f
(
x
)
{\displaystyle f(x)}
[ 주해 2] 정의역 으로 하고 미분계수를 치역 으로 하는 함수
f
′
(
x
)
{\displaystyle f'(x)}
도함수 라고 한다. 따라서, 미분에 의해 도함수를 구하는 과정은
f
(
x
)
→
f
′
(
x
)
{\displaystyle f(x)\to f'(x)}
사상 이다. 함수
f
(
x
)
{\displaystyle f(x)}
f
′
(
x
)
{\displaystyle f'(x)}
f
(
x
)
{\displaystyle f(x)}
x
{\displaystyle x}
[ 8]
미분의 개념을 이해하기 위해 높은 다리위에서 손에 쥐었던 농구공을 가만히 놓아 떨어뜨리는 것을 예로 들어보자.[ 9] 자유낙하 는 다음과 같은 결과를 얻을 것이다.
위의 평균변화율 예제에서 t의 변화량
Δ
t
{\displaystyle \Delta t}
순간변화율 이라 한다. 미분은 어떤 함수의 순간변화율을 구하는 계산 과정이고 한 지점에서의 순간변화율을 미분계수 라고 한다.[ 7] 함수의 극한 을 구하는 것과 같다.
일반적으로 함수 f(x)의 x에서의 순간변화율은 변화량인 Δ x가 0에 수렴될 때의 변화율이라고 생각할 수 있다. 이를 평균변화율에 견주어
d
d
x
f
(
x
)
{\displaystyle {\frac {d}{dx}}f(x)}
로 나타낸다. 이를 수식으로 표현하면
d
d
x
f
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
⋯
⋯
A
{\displaystyle {\frac {d}{dx}}f(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\cdots \cdots A}
이 된다.
위 에서 예를 든 자유낙하의 경우, 특정 시간 t에 대한 낙하거리의 순간변화율, 즉 순간속도는 다음과 같이 계산할 수 있다.
f
(
t
)
=
1
2
×
9.8
×
t
2
{\displaystyle f(t)={\frac {1}{2}}\times 9.8\times t^{2}}
k
=
1
2
×
9.8
{\displaystyle k={\frac {1}{2}}\times 9.8}
f
(
t
)
=
k
×
t
2
{\displaystyle f(t)=k\times t^{2}}
d
d
t
f
(
t
)
=
lim
Δ
t
→
0
f
(
t
+
Δ
t
)
−
f
(
t
)
Δ
t
{\displaystyle {\frac {d}{dt}}f(t)=\lim _{\Delta t\to 0}{\frac {f(t+\Delta t)-f(t)}{\Delta t}}}
=
lim
Δ
t
→
0
k
×
(
t
+
Δ
t
)
2
−
k
×
t
2
Δ
t
=
k
×
lim
Δ
t
→
0
(
t
+
Δ
t
)
2
−
t
2
Δ
t
{\displaystyle =\lim _{\Delta t\to 0}{\frac {k\times {(t+\Delta t)}^{2}-k\times t^{2}}{\Delta t}}=k\times \lim _{\Delta t\to 0}{\frac {{(t+\Delta t)}^{2}-t^{2}}{\Delta t}}}
=
k
×
lim
Δ
t
→
0
t
2
+
2
t
Δ
t
+
Δ
t
2
−
t
2
Δ
t
=
k
×
lim
Δ
t
→
0
2
t
Δ
t
+
Δ
t
2
Δ
t
{\displaystyle =k\times \lim _{\Delta t\to 0}{\frac {t^{2}+2t\Delta t+{\Delta t}^{2}-t^{2}}{\Delta t}}=k\times \lim _{\Delta t\to 0}{\frac {2t\Delta t+{\Delta t}^{2}}{\Delta t}}}
=
k
×
lim
Δ
t
→
0
2
t
+
Δ
t
{\displaystyle =k\times \lim _{\Delta t\to 0}2t+\Delta t}
Δ
t
{\displaystyle \Delta t}
=
k
×
2
t
{\displaystyle =k\times 2t}
k
=
1
2
×
9.8
{\displaystyle k={\frac {1}{2}}\times 9.8}
=
1
2
×
9.8
×
2
t
=
9.8
×
t
{\displaystyle ={\frac {1}{2}}\times 9.8\times 2t=9.8\times t}
d
d
t
f
(
t
)
=
9.8
×
t
{\displaystyle {\frac {d}{dt}}f(t)=9.8\times t}
위의 개요에서 살펴본 바와 같이 함수
f
(
x
)
=
k
x
2
{\displaystyle f(x)=kx^{2}}
f
′
(
x
)
=
2
k
x
{\displaystyle f'(x)=2kx}
도함수 라 한다. 일반적으로 다항 방정식을 관계식으로 하는 함수의 도함수는 미분 계산을 통하여 구할 수 있다. 즉, 함수 f(x)에 대한 도함수 f'(x)는 다음의 식으로 나타낼 수 있다.[ 10]
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
[ 주해 3] 도함수를 나타내는 기호는 여러 가지가 있다. 이는 미적분학의 발전 과정에서 여러 학자들이 각기 다른 기호를 제안하였기 때문이다. 널리 쓰이는 기호는 다음과 같다.[ 10]
기호
제안자
f
′
(
x
)
{\displaystyle \,f'(x)}
라그랑주
d
y
d
x
,
d
f
(
x
)
d
x
,
d
d
x
f
(
x
)
{\displaystyle {\frac {dy}{dx}},\quad {\frac {df(x)}{dx}},\;{\frac {d}{dx}}f(x)}
라이프니츠
x
˙
{\displaystyle {\dot {x}}}
뉴턴
D
f
(
x
)
{\displaystyle Df(x)}
오일러
일반적으로 도함수의 관계식 등을 표현할 때에는 라그랑주의
f
′
(
x
)
{\displaystyle \,f'(x)}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
=
g
(
t
)
{\displaystyle x=g(t)}
y
=
h
(
t
)
{\displaystyle y=h(t)}
[ 11]
d
y
d
t
=
(
d
y
d
x
)
⋅
(
d
x
d
t
)
{\displaystyle {\frac {dy}{dt}}=\left({\frac {dy}{dx}}\right)\cdot \left({\frac {dx}{dt}}\right)}
한편, 함수
f
(
x
)
{\displaystyle f(x)}
f
′
(
x
)
{\displaystyle f'(x)}
이계 미분 이라하고 그렇게 하여 얻은 함수를 이계도함수 라고 한다. 이계도함수는
f
″
(
x
)
{\displaystyle f''(x)}
[ 12] 고계도함수 (제n계도함수, 제n차함수)라 하고
f
n
(
x
)
{\displaystyle f^{n}(x)}
앞에서 다룬 농구공의 자유낙하 예제로 함수와 도함수, 이계 도함수의 관계를 살펴보면 다음과 같다.
함수 (
f
(
t
)
{\displaystyle f(t)\ }
도함수 (
f
′
(
t
)
{\displaystyle f'(t)\ }
이계 도함수 (
f
″
(
t
)
{\displaystyle f''(t)\ }
낙하 거리 (m )
순간 속도 (m /초 )
순간 가속도 (m /초 2 )
f
(
t
)
=
1
2
⋅
9.8
⋅
t
2
{\displaystyle f(t)={\frac {1}{2}}\cdot 9.8\cdot t^{2}}
f
′
(
t
)
=
d
d
t
f
(
t
)
=
9.8
⋅
t
{\displaystyle f'(t)={\frac {d}{dt}}f(t)=9.8\cdot t}
f
″
(
t
)
=
d
d
t
f
′
(
t
)
=
9.8
{\displaystyle f''(t)={\frac {d}{dt}}f'(t)=9.8}
주해:
↑ Δ x 를 증분(增分)이라고도 한다.
↑ 특정 구간은 함수 f(x)의 전체 구간일 수도 있고 일부 구간일 수도 있다.
↑ 예를 들어,
f
(
x
)
=
x
2
−
4
{\displaystyle f(x)=x^{2}-4\ }
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
=
lim
Δ
x
→
0
(
x
+
Δ
x
)
2
−
4
−
(
x
2
−
4
)
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{(x+\Delta x)}^{2}-4-(x^{2}-4)}{\Delta x}}}
=
lim
Δ
x
→
0
x
2
+
2
x
Δ
x
+
Δ
x
2
−
4
−
x
2
+
4
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {x^{2}+2x\Delta x+{\Delta x}^{2}-4-x^{2}+4}{\Delta x}}}
=
lim
Δ
x
→
0
2
x
Δ
x
+
Δ
x
2
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {2x\Delta x+{\Delta x}^{2}}{\Delta x}}}
=
lim
Δ
x
→
0
2
x
+
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}2x+\Delta x}
f
′
(
x
)
=
2
x
{\displaystyle f'(x)=2x\ }
함수의 그래프 에서 미분은 특정 지점에서 나타나는 접선 의 기울기를 뜻한다.[ 13]
y
=
|
x
|
{\displaystyle y=|x|\ }
미분은 함수 f(x)의 순간변화율을 계산하는 과정이다.
f
(
a
)
{\displaystyle f(a)}
f
′
(
a
)
{\displaystyle f'(a)}
미분 가능 이라고 한다. 미분이 가능하면 변화량은 연속이다. 그러나 그 역은 성립하지 않는다. 첨점과 같이 연속이지만 미분이 불가능한 경우가 존재한다. 예를 들어 함수
y
=
|
x
|
{\displaystyle y=|x|\ }
는 x=0 일때 연속이지만 미분은 불가능하다. 왜냐하면, 미분은 특정 지점에서 함수의 극한을 취하는 것으로 순간증가율과 순간감소율이 동일하다는 것을 전제로 하는데, 위의 함수의 경우 x=0 일때 순간감소율인 좌미분계수와 순간증가율인 우미분계수가 서로 다른 값을 갖게 되고 따라서 미분의 전제 조건을 충족할 수 없게 되어 미분이 불가능하게 된다.[ 14]
d
d
x
c
=
0
{\displaystyle {d \over dx}c=0}
d
d
x
x
=
1
{\displaystyle {d \over dx}x=1}
d
d
x
|
x
|
=
x
|
x
|
=
sgn
x
,
x
≠
0
{\displaystyle {d \over dx}|x|={x \over |x|}=\operatorname {sgn} x,\qquad x\neq 0}
d
d
x
x
c
=
c
x
c
−
1
{\displaystyle {d \over dx}x^{c}=cx^{c-1}}
d
d
x
x
=
1
2
x
{\displaystyle {d \over dx}{\sqrt {x}}={1 \over 2{\sqrt {x}}}}
d
d
x
(
1
x
)
=
−
1
x
2
{\displaystyle {d \over dx}\left({1 \over x}\right)=-{1 \over x^{2}}}
d
d
x
a
f
(
x
)
=
a
f
(
x
)
f
′
(
x
)
ln
a
,
a
>
0
{\displaystyle {d \over dx}a^{f(x)}={a^{f(x)}f'(x)\ln a},\qquad a>0}
d
d
x
c
x
=
c
x
ln
c
,
c
>
0
{\displaystyle {d \over dx}c^{x}={c^{x}\ln c},\qquad c>0}
d
d
x
e
x
=
e
x
{\displaystyle {d \over dx}e^{x}=e^{x}}
d
d
x
log
c
x
=
1
x
ln
c
,
c
>
0
,
c
≠
1
{\displaystyle {d \over dx}\log _{c}x={1 \over x\ln c},\qquad c>0,c\neq 1}
d
d
x
ln
x
=
1
x
{\displaystyle {d \over dx}\ln x={1 \over x}}
d
d
x
sin
x
=
cos
x
{\displaystyle {d \over dx}\sin x=\cos x}
d
d
x
cos
x
=
−
sin
x
{\displaystyle {d \over dx}\cos x=-\sin x}
d
d
x
tan
x
=
1
cos
2
x
=
sec
2
x
{\displaystyle {d \over dx}\tan x={1 \over \cos ^{2}x}=\sec ^{2}x}
d
d
x
csc
x
=
−
1
tan
x
sin
x
=
−
cot
x
csc
x
{\displaystyle {d \over dx}\csc x=-{1 \over \tan x\sin x}=-\cot x\csc x}
d
d
x
sec
x
=
tan
x
sec
x
{\displaystyle {d \over dx}\sec x=\tan x\sec x}
d
d
x
cot
x
=
−
1
sin
2
x
=
−
csc
2
x
{\displaystyle {d \over dx}\cot x=-{1 \over \sin ^{2}x}=-\csc ^{2}x}
d
d
x
sin
−
1
x
=
1
1
−
x
2
{\displaystyle {d \over dx}\sin ^{-1}x={1 \over {\sqrt {1-x^{2}}}}}
d
d
x
cos
−
1
x
=
−
1
1
−
x
2
{\displaystyle {d \over dx}\cos ^{-1}x={-1 \over {\sqrt {1-x^{2}}}}}
d
d
x
tan
−
1
x
=
1
1
+
x
2
{\displaystyle {d \over dx}\tan ^{-1}x={1 \over 1+x^{2}}}
d
d
x
csc
−
1
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {d \over dx}\csc ^{-1}x={-1 \over |x|{\sqrt {x^{2}-1}}}}
d
d
x
sec
−
1
x
=
1
|
x
|
x
2
−
1
{\displaystyle {d \over dx}\sec ^{-1}x={1 \over |x|{\sqrt {x^{2}-1}}}}
d
d
x
cot
−
1
x
=
−
1
1
+
x
2
{\displaystyle {d \over dx}\cot ^{-1}x={-1 \over 1+x^{2}}}
d
d
x
sinh
x
=
cosh
x
{\displaystyle {d \over dx}\sinh x=\cosh x}
d
d
x
cosh
x
=
sinh
x
{\displaystyle {d \over dx}\cosh x=\sinh x}
d
d
x
tanh
x
=
sech
2
x
{\displaystyle {d \over dx}\tanh x={\mbox{sech}}^{2}\,x}
d
d
x
csch
x
=
−
coth
x
csch
x
{\displaystyle {d \over dx}\,{\mbox{csch}}\,x=-\,{\mbox{coth}}\,x\,{\mbox{csch}}\,x}
d
d
x
sech
x
=
−
tanh
x
sech
x
{\displaystyle {d \over dx}\,{\mbox{sech}}\,x=-\tanh x\,{\mbox{sech}}\,x}
d
d
x
coth
x
=
−
csch
2
x
{\displaystyle {d \over dx}\,{\mbox{coth}}\,x=-\,{\mbox{csch}}^{2}\,x}
d
d
x
sinh
−
1
x
=
1
x
2
+
1
{\displaystyle {d \over dx}\sinh ^{-1}x={1 \over {\sqrt {x^{2}+1}}}}
d
d
x
cosh
−
1
x
=
1
x
2
−
1
{\displaystyle {d \over dx}\cosh ^{-1}x={1 \over {\sqrt {x^{2}-1}}}}
d
d
x
tanh
−
1
x
=
1
1
−
x
2
{\displaystyle {d \over dx}\tanh ^{-1}x={1 \over 1-x^{2}}}
d
d
x
csch
−
1
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {d \over dx}{\mbox{csch}}^{-1}\,x={-1 \over |x|{\sqrt {x^{2}-1}}}}
d
d
x
sech
−
1
x
=
1
x
1
−
x
2
{\displaystyle {d \over dx}{\mbox{sech}}^{-1}\,x={1 \over x{\sqrt {1-x^{2}}}}}
d
d
x
coth
−
1
x
=
1
1
−
x
2
{\displaystyle {d \over dx}{\mbox{coth}}^{-1}\,x={1 \over 1-x^{2}}}
f
(
x
)
=
c
{\displaystyle f(x)=c}
편집
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
c
−
c
Δ
x
=
0
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {c-c}{\Delta x}}=0}
y
=
c
f
(
x
)
{\displaystyle y=cf(x)}
편집
y
′
=
lim
Δ
x
→
0
c
f
(
x
+
Δ
x
)
−
c
f
(
x
)
Δ
x
=
c
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
c
f
′
(
x
)
{\displaystyle y'=\lim _{\Delta x\to 0}{\frac {cf(x+\Delta x)-cf(x)}{\Delta x}}=c\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}=cf'(x)}
n이 자연수인 경우,
인수분해를 이용하여
f
(
x
)
=
x
n
{\displaystyle f(x)={x^{n}}\ }
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
=
lim
Δ
x
→
0
(
x
+
Δ
x
)
n
−
x
n
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{(x+\Delta x)^{n}}-x^{n}}{\Delta x}}}
=
lim
Δ
x
→
0
(
x
+
Δ
x
−
x
)
(
x
n
−
1
+
x
n
−
2
(
x
+
Δ
x
)
+
x
n
−
3
(
x
+
Δ
x
)
2
+
.
.
.
+
(
x
+
Δ
x
)
n
−
1
)
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {(x+\Delta x-x)(x^{n-1}+x^{n-2}(x+\Delta x)+x^{n-3}(x+\Delta x)^{2}+...+(x+\Delta x)^{n-1})}{\Delta x}}}
=
lim
Δ
x
→
0
(
x
n
−
1
+
x
n
−
2
(
x
+
Δ
x
)
+
x
n
−
3
(
x
+
Δ
x
)
2
+
.
.
.
+
(
x
+
Δ
x
)
n
−
1
)
{\displaystyle =\lim _{\Delta x\to 0}{(x^{n-1}+x^{n-2}(x+\Delta x)+x^{n-3}(x+\Delta x)^{2}+...+(x+\Delta x)^{n-1})}}
Δ
x
{\displaystyle \Delta x}
=
x
n
−
1
+
x
n
−
1
+
.
.
.
+
x
n
−
1
=
n
x
n
−
1
{\displaystyle =x^{n-1}+x^{n-1}+...+x^{n-1}=nx^{n-1}\ }
f
′
(
x
)
=
n
x
n
−
1
{\displaystyle f'(x)=nx^{n-1}\ }
(
f
(
x
)
+
g
(
x
)
)
′
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
+
g
(
x
+
Δ
x
)
−
(
f
(
x
)
+
g
(
x
)
)
Δ
x
{\displaystyle (f(x)+g(x))'=\lim _{\Delta x\to 0}{\frac {{f(x+\Delta x)+g(x+\Delta x)}-(f(x)+g(x))}{\Delta x}}\ }
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
+
g
(
x
+
Δ
x
)
−
g
(
x
)
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)+g(x+\Delta x)-g(x)}{\Delta x}}\ }
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
+
lim
Δ
x
→
0
g
(
x
+
Δ
x
)
−
g
(
x
)
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{f(x+\Delta x)}-f(x)}{\Delta x}}+\lim _{\Delta x\to 0}{\frac {g(x+\Delta x)-g(x)}{\Delta x}}\ }
=
f
′
(
x
)
+
g
′
(
x
)
{\displaystyle =f'(x)+g'(x)\ }
같은 방법으로,
(
f
(
x
)
−
g
(
x
)
)
′
=
f
′
(
x
)
−
g
′
(
x
)
{\displaystyle (f(x)-g(x))'=f'(x)-g'(x)\ }
(
f
(
x
)
g
(
x
)
)
′
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
g
(
x
+
Δ
x
)
−
(
f
(
x
)
g
(
x
)
)
Δ
x
{\displaystyle (f(x)g(x))'=\lim _{\Delta x\to 0}{\frac {{f(x+\Delta x)g(x+\Delta x)}-(f(x)g(x))}{\Delta x}}\ }
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
g
(
x
+
Δ
x
)
−
f
(
x
)
g
(
x
+
Δ
x
)
+
f
(
x
)
g
(
x
+
Δ
x
)
−
(
f
(
x
)
g
(
x
)
)
Δ
x
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{f(x+\Delta x)g(x+\Delta x)}-{f(x)g(x+\Delta x)}+{f(x)g(x+\Delta x)}-(f(x)g(x))}{\Delta x}}\ }
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
lim
Δ
x
→
0
g
(
x
+
Δ
x
)
+
lim
Δ
x
→
0
g
(
x
+
Δ
x
)
−
g
(
x
)
Δ
x
lim
Δ
x
→
0
f
(
x
)
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\lim _{\Delta x\to 0}g(x+\Delta x)+\lim _{\Delta x\to 0}{\frac {g(x+\Delta x)-g(x)}{\Delta x}}\lim _{\Delta x\to 0}f(x)\ }
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
{\displaystyle =f'(x)g(x)+f(x)g'(x)\ }
삼각함수 의 미분 역시 다항식의 미분과 같이 함수의 극한을 통해 계산할 수 있다. 예를 들어
f
(
x
)
=
sin
x
{\displaystyle f(x)=\sin {x}}
[ 15]
도함수의 정의에 의해
f
′
(
x
)
=
lim
Δ
x
→
0
sin
(
x
+
Δ
x
)
−
sin
x
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {\sin {(x+\Delta x)}-\sin {x}}{\Delta x}}}
이때,
sin
A
−
sin
B
=
2
cos
(
A
+
B
2
)
sin
(
A
−
B
2
)
{\displaystyle \sin {A}-\sin {B}=2\cos \left({\frac {A+B}{2}}\right)\sin \left({\frac {A-B}{2}}\right)}
이므로, 위의 도함수는 다음과 같이 쓸 수 있다.
f
′
(
x
)
=
lim
Δ
x
→
0
2
cos
(
x
+
Δ
x
2
)
sin
(
Δ
x
2
)
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {2\cos \left(x+{\frac {\Delta x}{2}}\right)\sin \left({\frac {\Delta x}{2}}\right)}{\Delta x}}}
=
lim
Δ
x
→
0
cos
(
x
+
Δ
x
2
)
⋅
lim
Δ
x
→
0
sin
(
Δ
x
2
)
Δ
x
2
{\displaystyle =\lim _{\Delta x\to 0}{\cos \left(x+{\frac {\Delta x}{2}}\right)}\cdot \lim _{\Delta x\to 0}{\frac {\sin \left({\frac {\Delta x}{2}}\right)}{\frac {\Delta x}{2}}}}
한편,
lim
x
→
0
sin
x
x
=
1
{\displaystyle \lim _{x\to 0}{\frac {\sin {x}}{x}}=1}
이므로
lim
Δ
x
→
0
sin
(
Δ
x
2
)
Δ
x
2
=
1
{\displaystyle \lim _{\Delta x\to 0}{\frac {\sin \left({\frac {\Delta x}{2}}\right)}{\frac {\Delta x}{2}}}=1}
이다. 따라서 위의 도함수는
f
′
(
x
)
=
lim
Δ
x
→
0
cos
(
x
+
Δ
x
2
)
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\cos \left(x+{\frac {\Delta x}{2}}\right)}}
가 된다.
Δ
x
{\displaystyle \Delta x}
f
′
(
x
)
=
cos
x
{\displaystyle f'(x)=\cos {x}\ }
위와 같은 방법을 통해 다른 삼각함수에 대해서도 도함수를 구할 수 있다. 다음은 각 종 삼각함수의 도함수이다.
(
sin
(
x
)
)
′
=
cos
(
x
)
{\displaystyle \left(\sin(x)\right)'=\cos(x)}
(
cos
(
x
)
)
′
=
−
sin
(
x
)
{\displaystyle \left(\cos(x)\right)'=-\sin(x)}
(
tan
(
x
)
)
′
=
(
sin
(
x
)
cos
(
x
)
)
′
=
cos
2
(
x
)
+
sin
2
(
x
)
cos
2
(
x
)
=
1
cos
2
(
x
)
=
sec
2
(
x
)
{\displaystyle \left(\tan(x)\right)'=\left({\frac {\sin(x)}{\cos(x)}}\right)'={\frac {\cos ^{2}(x)+\sin ^{2}(x)}{\cos ^{2}(x)}}={\frac {1}{\cos ^{2}(x)}}=\sec ^{2}(x)}
(
cot
(
x
)
)
′
=
(
cos
(
x
)
sin
(
x
)
)
′
=
−
sin
2
(
x
)
−
cos
2
(
x
)
sin
2
(
x
)
=
−
(
1
+
cot
2
(
x
)
)
=
−
csc
2
(
x
)
{\displaystyle \left(\cot(x)\right)'=\left({\frac {\cos(x)}{\sin(x)}}\right)'={\frac {-\sin ^{2}(x)-\cos ^{2}(x)}{\sin ^{2}(x)}}=-(1+\cot ^{2}(x))=-\csc ^{2}(x)}
(
sec
(
x
)
)
′
=
(
1
cos
(
x
)
)
′
=
sin
(
x
)
cos
2
(
x
)
=
1
cos
(
x
)
.
sin
(
x
)
cos
(
x
)
=
sec
(
x
)
tan
(
x
)
{\displaystyle \left(\sec(x)\right)'=\left({\frac {1}{\cos(x)}}\right)'={\frac {\sin(x)}{\cos ^{2}(x)}}={\frac {1}{\cos(x)}}.{\frac {\sin(x)}{\cos(x)}}=\sec(x)\tan(x)}
(
csc
(
x
)
)
′
=
(
1
sin
(
x
)
)
′
=
−
cos
(
x
)
sin
2
(
x
)
=
−
1
sin
(
x
)
.
cos
(
x
)
sin
(
x
)
=
−
csc
(
x
)
cot
(
x
)
{\displaystyle \left(\csc(x)\right)'=\left({\frac {1}{\sin(x)}}\right)'=-{\frac {\cos(x)}{\sin ^{2}(x)}}=-{\frac {1}{\sin(x)}}.{\frac {\cos(x)}{\sin(x)}}=-\csc(x)\cot(x)}
(
arcsin
(
x
)
)
′
=
1
1
−
x
2
{\displaystyle \left(\arcsin(x)\right)'={\frac {1}{\sqrt {1-x^{2}}}}}
(
arccos
(
x
)
)
′
=
−
1
1
−
x
2
{\displaystyle \left(\arccos(x)\right)'={\frac {-1}{\sqrt {1-x^{2}}}}}
(
arctan
(
x
)
)
′
=
1
x
2
+
1
{\displaystyle \left(\arctan(x)\right)'={\frac {1}{x^{2}+1}}}
지수 함수
f
(
x
)
=
b
x
{\displaystyle f(x)=b^{x}}
f
′
(
x
)
{\displaystyle f'(x)}
[ 16]
Δ
x
{\displaystyle \Delta x}
h
{\displaystyle h}
f
′
(
x
)
=
lim
h
→
0
b
x
+
h
−
b
x
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {b^{x+h}-b^{x}}{h}}}
지수 법칙에 의해
b
x
+
h
−
b
x
=
b
x
b
h
−
b
x
=
b
x
(
b
h
−
1
)
{\displaystyle b^{x+h}-b^{x}=b^{x}b^{h}-b^{x}=b^{x}(b^{h}-1)\ }
이므로,
f
′
(
x
)
=
lim
h
→
0
b
x
(
b
h
−
1
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {b^{x}(b^{h}-1)}{h}}}
=
b
x
lim
h
→
0
b
h
−
1
h
{\displaystyle =b^{x}\lim _{h\to 0}{\frac {b^{h}-1}{h}}}
이때 상수
k
{\displaystyle k}
ln
b
=
lim
h
→
0
b
h
−
1
h
{\displaystyle \ln b=\lim _{h\to 0}{\frac {b^{h}-1}{h}}}
와 같이 정의하면,
f
′
(
x
)
=
b
x
ln
b
{\displaystyle f'(x)=b^{x}\ln b\ }
가 된다.
한편 b = e 일때
lim
h
→
0
e
h
−
1
h
=
1
{\displaystyle \lim _{h\to 0}{\frac {e^{h}-1}{h}}=1}
이 되므로,
f
(
x
)
=
e
x
{\displaystyle f(x)=e^{x}}
f
′
(
x
)
=
e
x
{\displaystyle f'(x)=e^{x}}
f
(
x
)
=
log
a
x
{\displaystyle f(x)=\log _{a}x}
x
=
a
f
(
x
)
{\displaystyle x=a^{f(x)}}
합성함수의 미분법에 의해,
1
=
a
f
(
x
)
f
′
(
x
)
ln
a
{\displaystyle 1={a^{f(x)}}f'(x)\ln a}
f
′
(
x
)
=
1
a
f
(
x
)
ln
a
=
1
x
ln
a
{\displaystyle f'(x)={\frac {1}{a^{f(x)}\ln a}}={\frac {1}{x\ln a}}}
x=e인 경우
f
(
x
)
=
ln
x
{\displaystyle f(x)=\ln x}
f
′
(
x
)
=
1
x
ln
e
=
1
x
{\displaystyle f'(x)={\frac {1}{x\ln e}}={\frac {1}{x}}}
적분의 예 적분 (積分)은 리만 적분 에서 다루는 고전적인 정의에 따르면 실수 의 척도를 사용하는 측도 공간 에 나타낼 수 있는 연속인 함수 f(x)에 대하여 그 함수의 정의역 의 부분 집합 을 이루는 구간 [a, b] 에 대응하는 치역 으로 이루어진 곡선 의 리만 합 의 극한 을 구하는 것이다. 이를 정적분이라 한다. 구간 [a, b]에 대하여
f
(
x
)
≧
0
{\displaystyle f(x)\geqq 0}
[ 17]
이를 수식으로 나타내면, 폐구간
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
{\displaystyle f(x)}
[ 17]
∫
a
b
f
(
x
)
d
x
=
lim
n
→
∞
∑
k
=
1
n
f
(
x
k
)
Δ
x
(
x
k
=
a
+
k
Δ
x
,
Δ
x
=
b
−
a
n
)
{\displaystyle \int _{a}^{b}f(x)dx=\lim _{n\to \infty }\sum _{k=1}^{n}f(x_{k})\Delta x\quad \left(x_{k}=a+k\Delta x,\ \Delta x={\frac {b-a}{n}}\right)}
적분은 곡면으로 이루어진 도형의 넓이나 물체의 부피와 같은 것에서 중력의 중심을 구하는 문제에 이르기까지 폭넓게 사용된다. 예를 들어 곡면으로 이루어진 수영장을 채우기 위해 얼마만큼의 물이 필요한지를 계산할 수 있다.
임의의 함수
f
(
x
)
{\displaystyle f(x)}
[
a
,
b
]
{\displaystyle [a,b]}
0
{\displaystyle 0}
0
{\displaystyle 0}
0부터 1까지 √x 의 적분의 근사값을 5개의 ■ 와 12개의 ■ 로 계산한 모양 y = f (x ) 인 곡선에서 x = 0 에서 x = 1 사이의 넓이를 구하는 경우를 가정할 때, f (x ) = √x 라면. 이것은 다음과 같은 적분식으로 표현할 수 있다.
∫
0
1
x
d
x
.
{\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx\,\!.}
이제 다음과 같은 방법에 따라 위 식이 나타내는 넓이를 구할 수 있다. 우선
f
(
0
)
=
0
{\displaystyle f(0)=0}
f
(
1
)
=
1
{\displaystyle f(1)=1}
[
0
,
1
]
{\displaystyle [0,1]}
0.2
×
(
0.2
+
0.4
+
0.6
+
0.8
+
1
)
{\displaystyle 0.2\times ({\sqrt {0.2}}+{\sqrt {0.4}}+{\sqrt {0.6}}+{\sqrt {0.8}}+{\sqrt {1}})}
≈
0.2
×
(
0.4472
+
0.6325
+
0.7746
+
0.8944
+
1
)
=
0.7497.
{\displaystyle \approx 0.2\times (0.4472+0.6325+0.7746+0.8944+1)=0.7497.\,\!}
이 된다. 그래프에서 나타난 것과 같이 이 사각형들의 넓이의 합은 실제 넓이보다 여전히 크다.
한편, 오른쪽 그래프의 녹색 사각형은 구간 [0,1]을 12등분하여 왼쪽 값을 높이로 하는 사각형을 그린 것이다. 이 사각형들의 넓이의 합은
1
12
×
(
0
12
+
1
12
+
⋯
+
11
12
)
≈
0.6203.
{\displaystyle {\frac {1}{12}}\times \left({\sqrt {\frac {0}{12}}}+{\sqrt {\frac {1}{12}}}+\cdots +{\sqrt {\frac {11}{12}}}\right)\approx 0.6203.\,\!}
이다. 이 경우에는 사각형들의 넓이의 합은 실제 곡선의 넓이보다 작다.
이렇게 작게 나눈 구간의 오른쪽을 사각형의 높이로 삼으면 실제 곡선의 넓이보다 크게 되고 왼쪽을 사각형의 높이로 삼으면 실제 곡선의 넓이보다 작게된다. 그러나, 작게 나눈 구간의 폭을 매우 작게 만들면 둘의 차이는 거의 없게 되고 곡선의 실제 넓이에 근사하게 된다.
이와 같이 적분은 곡선의 넓이를 구하기 위해 밑변의 길이가 0으로 수렴하는 무수히 많은 사각형들의 넓이를 합한 것과 같다. 다항식을 관계식으로 하는 함수의 적분 계산법에 따라 구간 [0,1]에서 f (x ) = √x 의 적분은 다음과 같이 계산된다.
∫
0
1
x
d
x
=
∫
0
1
x
1
2
d
x
=
F
(
1
)
−
F
(
0
)
=
2
3
.
≈
0.6667.
{\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx=\int _{0}^{1}x^{\frac {1}{2}}\,dx=F(1)-F(0)={\textstyle {\frac {2}{3}}}.\approx 0.6667.\,\!}
F
(
x
)
=
2
3
x
3
2
{\displaystyle F(x)={\frac {2}{3}}x^{\frac {3}{2}}}
계산의 자세한 방법은 이 글의 〈표기와 계산〉 항목에 있다.
지금까지의 예제는 리만 적분 에 따른 것이다. 리만 적분에서 함수 f(x)의 적분은 다음과 같이 표기한다.
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx\,\!}
이때 ∫ 는 S 를 변형시킨 것으로 합한다(영어 : summation )는 것을 나타내는 적분 기호이고 f(x)는 함수를 dx 는 x의 구간에 대한 변화량(영어 : differentials )을 곱한다는 의미를 지닌다.
일반적인 리만 합은 주어진 구간을 불규칙하게 분할한다. 이 그래프에서 최대 분할 구간(x축의 빨간색 구간)의 경우 참 값은 3.76이나 리만 합은 3.648 이다. 리만 적분은 주어진 구간에서 리만 합 의 극한으로 적분을 정의한다. 폐구간 [a,b]는 다음과 같이 보다 작은 구간으로 분할 될 수 있다.
a
=
x
0
≦
t
1
≦
x
1
≦
t
2
≦
x
2
≦
⋯
≦
x
n
−
1
≦
t
n
≦
x
n
=
b
.
{\displaystyle a=x_{0}\leqq t_{1}\leqq x_{1}\leqq t_{2}\leqq x_{2}\leqq \cdots \leqq x_{n-1}\leqq t_{n}\leqq x_{n}=b.\,\!}
리만 합의 종류 ■ 오른쪽 리만 합, ■ 최솟값 리만 합, ■ 최댓값 리만 합, ■ 왼쪽 리만 합. 구간 [a,b]를 n 개의 하위 구간으로 분할하는 경우, 하위 구간들은 [x i −1x i i 에 의해 표기될 수 있다. 분할된 각각의 하위 구간의 표시는, t i x i −1x i
∑
i
=
1
n
f
(
t
i
)
Δ
i
;
{\displaystyle \sum _{i=1}^{n}f(t_{i})\Delta _{i};}
왼쪽의 그래프와 같이 각각의 하위 구간들은 사각형을 구성하게 된다. 이때 곡선과 만나는 어느 지점을 사각형의 높이로 삼을 것인지에 따라 사각형의 크기가 달라지게 된다. 예를 들어 하위 구간의 시작점을 기준으로 한다면 그래프에서는 왼쪽을 기준으로 한 사각형을 그릴 수 있다. 이 경우를 왼쪽 리만 합이라고 한다. 같은 방법으로 하위 구간의 끝점을 기준으로 하는 오른쪽 리만 합, 가운데 지점을 기준으로 하는 가운데 리만 합, 하위 구간에서 곡선의 가장 높은 곳을 기준으로 하는 최댓값 리만 합 등을 만들 수 있다. 왼쪽의 그림에서 가운데에 있는 그래프는 오른쪽 리만 합이든 다른 종류의 리만 합이든 종류에 관계없이 극한을 취할 경우 같은 값으로 수렴함을 보여주고 있다.
구간 [a,b]에 대하여 k 를 간격으로 하여 n 개로 분할된 하위 구간의 변량을 Δk x k x k −1k [ 18] [ 19]
∫
a
b
f
(
x
)
d
x
=
lim
n
→
∞
∑
k
=
1
n
f
(
x
k
)
Δ
x
(
x
k
=
a
+
k
Δ
x
,
Δ
x
=
b
−
a
n
)
{\displaystyle \int _{a}^{b}f(x)dx=\lim _{n\to \infty }\sum _{k=1}^{n}f(x_{k})\Delta x\quad \left(x_{k}=a+k\Delta x,\ \Delta x={\frac {b-a}{n}}\right)}
미적분학의 기본정리 에 따라 적분은 미분의 역산이다. 즉, 함수
f
(
x
)
=
x
{\displaystyle f(x)=x}
도함수 로 하는 원시함수
F
(
x
)
{\displaystyle F(x)}
부정적분 (不定積分)이라 한다. 이를 식으로 나타내면 다음과 같은 관계가 성립한다.[ 20]
d
d
x
F
(
x
)
=
f
(
x
)
{\displaystyle {\frac {d}{dx}}F(x)=f(x)}
예를 들어,
f
(
x
)
=
x
{\displaystyle f(x)=x}
F
(
x
)
{\displaystyle F(x)}
d
d
x
F
(
x
)
=
x
{\displaystyle {\frac {d}{dx}}F(x)=x\ }
이 때 도함수가
f
(
x
)
=
x
{\displaystyle f(x)=x}
F
(
x
)
{\displaystyle F(x)}
F
(
x
)
=
A
x
2
+
B
x
+
C
{\displaystyle F(x)=Ax^{2}+Bx+C\ }
의 형태가 됨을 알 수 있다. 따라서, 다항식의 도함수 계산법을 이용하면
2
A
=
1
,
B
=
0
{\displaystyle 2A=1,B=0}
C
{\displaystyle C}
F
(
x
)
=
1
2
x
2
+
C
{\displaystyle F(x)={\frac {1}{2}}x^{2}+C\ }
위 식에서 나타나는 임의의 상수
C
{\displaystyle C}
F
(
x
)
{\displaystyle F(x)}
f
(
x
)
{\displaystyle f(x)}
0
{\displaystyle 0}
[ 21]
일반적으로,
f
(
x
)
=
a
0
x
n
+
a
1
x
n
−
1
+
⋯
+
a
n
{\displaystyle f(x)=a_{0}x^{n}+a_{1}x^{n-1}+\cdots +a_{n}}
n
≠
−
1
{\displaystyle n\neq -1}
의 꼴을 갖는 다항식을 관계식으로 하는 함수의 원시 함수 F(x)는 다음과 같은 형태가 된다.[ 22]
F
(
x
)
=
a
0
n
+
1
x
n
+
1
+
a
1
n
x
n
+
⋯
+
a
n
x
+
C
{\displaystyle F(x)={\frac {a_{0}}{n+1}}x^{n+1}+{\frac {a_{1}}{n}}x^{n}+\cdots +a_{n}x+C}
일반적인 경우를 살펴보자. 구간 [a, b]에서 적분 가능한 함수
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
{\displaystyle F(x)}
G
(
x
)
{\displaystyle G(x)}
H
(
x
)
=
F
(
x
)
−
G
(
x
)
{\displaystyle H(x)=F(x)-G(x)}
(
a
,
b
]
{\displaystyle (a,b]}
x
{\displaystyle x}
H
(
x
)
{\displaystyle H(x)}
H
(
x
)
−
H
(
a
)
x
−
a
=
H
′
(
c
)
{\displaystyle {\frac {H(x)-H(a)}{x-a}}=H'(c)}
를 만족하는 c가 구간 (a, x)에 존재한다. 그런데
H
′
(
c
)
=
F
′
(
c
)
−
G
′
(
c
)
=
f
(
c
)
−
f
(
c
)
=
0
{\displaystyle H'(c)=F'(c)-G'(c)=f(c)-f(c)=0}
이므로
H
(
x
)
−
H
(
a
)
=
0
{\displaystyle H(x)-H(a)=0}
이다. 즉 H(x) = H(a)이다. 구간 (a, b]에 속하는 임의의 x를 택하였으므로, 구간 [a, b]에서 이 식이 성립한다. 즉, 구간 [a, b]에서 H(x)는 상수함수이다. 따라서 H(x) = k (k는 상수)라 할 수 있으므로
F
(
x
)
−
G
(
x
)
=
H
(
x
)
=
k
{\displaystyle F(x)-G(x)=H(x)=k}
이다. 즉, 구간 [a, b]에서 두 함수 F(x)와 G(x)는 상수만큼 차이난다. 따라서 함수 f(x)의 임의의 부정적분 F(x)와 G(x)는 상수만큼 차이난다. 어떤 함수의 부정적분을 적분상수를 이용하여 표기하는 것이 정당함을 알 수 있다.
한편, 함수 f(x)의 구간 [a, b]에 대한 적분은 시작점과 끝점이 있는 유계의 변화량을 뜻하며 이를 정적분 (定積分)이라 한다. 구간 [a, b]에 대한 함수 f(x)의 정적분은 다음과 같이 계산될 수 있다. 일반적으로 적분은 정적분을 가리킨다. 또한, 리만 합 의 극한으로서 정적분을 정의하는 것을 리만 적분 이라고 하며, 별다른 설명이 없을 경우 적분은 흔히 리만 적분을 가리킨다.[ 23]
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)dx=F(b)-F(a)}
(단,
F
(
x
)
{\displaystyle F(x)\ }
f
(
x
)
{\displaystyle f(x)\ }
구간 [4,9]에 대한 f(x)=x 의 정적분 위에서 예를 든 f(x)=x 의 구간 [4, 9] 에 대한 적분을 계산하면,
∫
4
9
x
d
x
=
F
(
9
)
−
F
(
4
)
=
1
2
⋅
9
2
+
C
−
(
1
2
⋅
4
2
+
C
)
{\displaystyle \int _{4}^{9}xdx=F(9)-F(4)={\frac {1}{2}}\cdot 9^{2}+C-\left({\frac {1}{2}}\cdot 4^{2}+C\right)}
=
9
2
2
−
4
2
2
=
81
−
16
2
=
65
2
=
32.5
{\displaystyle ={\frac {9^{2}}{2}}-{\frac {4^{2}}{2}}={\frac {81-16}{2}}={\frac {65}{2}}=32.5}
구간 [4, 9]에 대한 함수 f(x)=x의 치역은 모두 양수 이므로 위 결과는 구간 [4, 9]에 대한 f(x)=x 의 넓이와 같다. 오른쪽의 그래프와 같이 이는 결국 한변의 길이가 9인 직각이등변삼각형의 넓이에서 한변의 길이가 4인 직각이등변삼각형의 넓이를 뺀 것과 동일하고, 그 결과 역시 같다.
위의 예와 같이 적분은 하나의 수 로서
x
{\displaystyle x\ }
[ 23]
∫
a
b
f
(
x
)
d
x
=
∫
a
b
f
(
y
)
d
y
=
∫
a
b
f
(
z
)
d
z
=
⋯
{\displaystyle \int _{a}^{b}f(x)dx=\int _{a}^{b}f(y)dy=\int _{a}^{b}f(z)dz=\cdots }
함수 ƒ (x ) = (x3 /3)-(x2 /2)-x+c의 기울기장(slope field )의 그림. 적분 상수 C 를 바꾸어서 무한히 많은 해 중에 세 개의 해를 보여주고 있다. 미적분학에서 함수
f
{\displaystyle f}
부정적분 (indefinite integral) 또는 역도함수 (antiderivative)는 미분을 하여
f
{\displaystyle f}
F
{\displaystyle F}
미적분학의 기본정리 (fundamental theorem of calculus)를 통해 정적분 (definite integrals)과 연결된다. 즉, 어떤 구간을 따라서 어떤 함수의 정적분을 계산한 값은 그 함수의 부정적분에 구간의 양 끝 값을 대입한 값의 차와 같게 된다.
좀 더 다양한 공식은
적분표 문서를 참고하십시오.
부정적분은 미분의 역과정을 수행하면 된다. 기호
∫
{\displaystyle \textstyle \int }
∫
f
(
x
)
d
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)\,dx=F(x)+C}
이때,
F
′
(
x
)
=
d
d
x
F
(
x
)
=
f
(
x
)
.
{\displaystyle F'\!(x)={\frac {d}{dx}}F(x)=f(x).}
가 된다. 여기서
C
{\displaystyle C}
적분상수 (Constant of integration)가 된다.
부정적분은 미분의 역과정이므로 미분 공식과 밀접한 연관이 있다. 유용한 공식으로는 다음과 같은 것들이 있다.
∫
d
x
=
x
+
C
{\displaystyle \int dx=x+C}
상수배한 함수의 부정적분은 부정적분한 함수의 상수배와 같다.
∫
a
f
(
x
)
d
x
=
a
∫
f
(
x
)
d
x
{\displaystyle \int af(x)\,dx=a\int f(x)\,dx}
같은 구간에 정의된 두 함수의 합을 부정적분한 것은 각각 부정적분 한 함수의 합과 같다.
∫
[
f
(
x
)
+
g
(
x
)
]
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
{\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}
n
{\displaystyle n}
단항식 은 다음과 같이 적분된다.
∫
x
n
d
x
=
{
x
n
+
1
n
+
1
+
C
,
if
n
≠
−
1
ln
|
x
|
+
C
,
if
n
=
−
1
{\displaystyle \int x^{n}\,dx={\begin{cases}{\frac {x^{n+1}}{n+1}}+C,&{\text{if }}n\neq -1\\\ln |x|+C,&{\text{if }}n=-1\end{cases}}}
부정적분은 미적분학의 기본정리 (fundamental theorem of calculus)를 이용하여 정적분 (definite integral)을 계산할 때 매우 유용하다. 즉,
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)dx=F(b)-F(a)}
이런 계산결과의 관계 덕분에 역도함수는 구간이 정해지지 않은 적분이므로 부 정적분(in definite integral) 이라는 용어를 쓰게 된다. 즉, 구간을 정하지 않은 다음과 같은 기호로 표시하게 된다.
∫
f
(
x
)
d
x
{\displaystyle \int f(x)dx}
모든 상수는 미분하면 사라진다. 그러므로 주어진 함수의 역도함수는 어떤 상수항도 취할 수 있게 된다. 따라서 역도함수의 마지막에 임의의 상수가 온다는 의미로 임의의 적분상수
C
{\displaystyle C}
역도함수가 존재하지만 그 역도함수를 초등함수 (Elementary function)로 표현할 수 없는 함수도 많이 있다. 다음과 같은 예가 있다.
∫
e
−
x
2
d
x
,
∫
sin
(
x
)
x
d
x
,
∫
1
ln
x
d
x
,
∫
x
x
d
x
.
{\displaystyle \int e^{-x^{2}}\,dx,\qquad \int {\frac {\sin(x)}{x}}\,dx,\qquad \int {\frac {1}{\ln x}}\,dx,\qquad \int x^{x}\,dx.}
∫
a
f
(
x
)
d
x
=
a
∫
f
(
x
)
d
x
(
a
constant)
{\displaystyle \int af(x)\,dx=a\int f(x)\,dx\qquad {\mbox{(}}a{\mbox{ constant)}}\,\!}
∫
[
f
(
x
)
+
g
(
x
)
]
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
{\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}
∫
f
(
x
)
g
(
x
)
d
x
=
f
(
x
)
∫
g
(
x
)
d
x
−
∫
[
f
′
(
x
)
(
∫
g
(
x
)
d
x
)
]
d
x
{\displaystyle \int f(x)g(x)\,dx=f(x)\int g(x)\,dx-\int \left[f'(x)\left(\int g(x)\,dx\right)\right]\,dx}
∫
[
f
(
x
)
]
n
f
′
(
x
)
d
x
=
[
f
(
x
)
]
n
+
1
n
+
1
+
C
(for
n
≠
−
1
)
{\displaystyle \int [f(x)]^{n}f'(x)\,dx={[f(x)]^{n+1} \over n+1}+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}
∫
f
′
(
x
)
f
(
x
)
d
x
=
ln
|
f
(
x
)
|
+
C
{\displaystyle \int {f'(x) \over f(x)}\,dx=\ln {\left|f(x)\right|}+C}
∫
f
′
(
x
)
f
(
x
)
d
x
=
1
2
[
f
(
x
)
]
2
+
C
{\displaystyle \int {f'(x)f(x)}\,dx={1 \over 2}[f(x)]^{2}+C}
∫
x
n
d
x
=
x
n
+
1
n
+
1
+
C
if
n
≠
−
1
{\displaystyle \int x^{n}\,dx={\frac {x^{n+1}}{n+1}}+C\qquad {\mbox{ if }}n\neq -1}
∫
x
−
1
d
x
=
ln
|
x
|
+
C
{\displaystyle \int x^{-1}\,dx=\ln {\left|x\right|}+C}
∫
1
1
+
x
2
d
x
=
arctan
x
+
C
{\displaystyle \int {\frac {1}{1+x^{2}}}\,dx=\arctan {x}+C}
∫
1
1
−
x
2
d
x
=
arcsin
x
+
C
{\displaystyle \int {1 \over {\sqrt {1-x^{2}}}}\,dx=\arcsin {x}+C}
∫
−
1
1
−
x
2
d
x
=
arccos
x
+
C
{\displaystyle \int {-1 \over {\sqrt {1-x^{2}}}}\,dx=\arccos {x}+C}
∫
1
|
x
|
x
2
−
1
d
x
=
arcsec
x
+
C
{\displaystyle \int {1 \over |x|{\sqrt {x^{2}-1}}}\,dx={\mbox{arcsec}}\,{x}+C}
∫
ln
x
d
x
=
x
ln
x
−
x
+
C
{\displaystyle \int \ln {x}\,dx=x\ln {x}-x+C}
∫
log
a
x
d
x
=
x
log
a
x
−
x
ln
a
+
C
{\displaystyle \int \log _{a}x\,dx=x\log _{a}x-{\frac {x}{\ln a}}+C}
∫
e
x
d
x
=
e
x
+
C
{\displaystyle \int e^{x}\,dx=e^{x}+C}
∫
a
x
d
x
=
a
x
ln
a
+
C
{\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln {a}}}+C}
∫
cos
x
d
x
=
sin
x
+
C
{\displaystyle \int \cos {x}\,dx=\sin {x}+C}
∫
sin
x
d
x
=
−
cos
x
+
C
{\displaystyle \int \sin {x}\,dx=-\cos {x}+C}
∫
tan
x
d
x
=
−
ln
|
cos
x
|
+
C
{\displaystyle \int \tan {x}\,dx=-\ln {\left|\cos {x}\right|}+C}
∫
csc
x
d
x
=
ln
|
csc
x
−
cot
x
|
+
C
{\displaystyle \int \csc {x}\,dx=\ln {\left|\csc {x}-\cot {x}\right|}+C}
∫
sec
x
d
x
=
ln
|
sec
x
+
tan
x
|
+
C
{\displaystyle \int \sec {x}\,dx=\ln {\left|\sec {x}+\tan {x}\right|}+C}
∫
cot
x
d
x
=
ln
|
sin
x
|
+
C
{\displaystyle \int \cot {x}\,dx=\ln {\left|\sin {x}\right|}+C}
∫
sec
2
x
d
x
=
tan
x
+
C
{\displaystyle \int \sec ^{2}x\,dx=\tan x+C}
∫
csc
2
x
d
x
=
−
cot
x
+
C
{\displaystyle \int \csc ^{2}x\,dx=-\cot x+C}
∫
sin
2
m
x
d
x
=
1
2
m
(
m
x
−
sin
m
x
cos
m
x
)
+
C
{\displaystyle \int \sin ^{2}mx\,dx={{\frac {1}{2m}}(mx-\sin mx\cos mx)}+C}
∫
cos
2
m
x
d
x
=
1
2
m
(
m
x
+
sin
m
x
cos
m
x
)
+
C
{\displaystyle \int \cos ^{2}mx\,dx={{\frac {1}{2m}}(mx+\sin mx\cos mx)}+C}
∫
sin
n
x
d
x
=
−
sin
n
−
1
x
cos
x
n
+
n
−
1
n
∫
sin
n
−
2
x
d
x
+
C
{\displaystyle \int \sin ^{n}x\,dx={-{\frac {\sin ^{n-1}x\cos x}{n}}+{\frac {n-1}{n}}\int \sin ^{n-2}x\,dx}+C}
∫
cos
n
x
d
x
=
cos
n
−
1
x
sin
x
n
+
n
−
1
n
∫
cos
n
−
2
x
d
x
+
C
{\displaystyle \int \cos ^{n}x\,dx={{\frac {\cos ^{n-1}x\sin x}{n}}+{\frac {n-1}{n}}\int \cos ^{n-2}x\,dx}+C}
∫
sec
n
x
d
x
=
sec
n
−
2
x
tan
x
n
−
1
+
n
−
2
n
−
1
∫
sec
n
−
2
x
d
x
+
C
{\displaystyle \int \sec ^{n}x\,dx={{\frac {\sec ^{n-2}x\tan x}{n-1}}+{\frac {n-2}{n-1}}\int \sec ^{n-2}x\,dx}+C}
∫
csc
n
x
d
x
=
csc
n
−
2
x
cot
x
−
(
n
−
1
)
+
n
−
2
n
−
1
∫
csc
n
−
2
x
d
x
+
C
{\displaystyle \int \csc ^{n}x\,dx={{\frac {\csc ^{n-2}x\cot x}{-(n-1)}}+{\frac {n-2}{n-1}}\int \csc ^{n-2}x\,dx}+C}
∫
sinh
x
d
x
=
cosh
x
+
C
{\displaystyle \int \sinh x\,dx=\cosh x+C}
∫
cosh
x
d
x
=
sinh
x
+
C
{\displaystyle \int \cosh x\,dx=\sinh x+C}
∫
tanh
x
d
x
=
ln
(
cosh
x
)
+
C
{\displaystyle \int \tanh x\,dx=\ln(\cosh x)+C}
∫
csch
x
d
x
=
ln
|
tanh
x
2
|
+
C
{\displaystyle \int {\mbox{csch}}\,x\,dx=\ln \left|\tanh {x \over 2}\right|+C}
∫
sech
x
d
x
=
arctan
(
sinh
x
)
+
C
{\displaystyle \int {\mbox{sech}}\,x\,dx=\arctan(\sinh x)+C}
∫
coth
x
d
x
=
ln
|
sinh
x
|
+
C
{\displaystyle \int \coth x\,dx=\ln |\sinh x|+C}
어떤 함수의 적분은 원시 함수 로 나타낼 수 없지만, 특정 구간에서의 적분값을 계산할 수는 있다. 다음은 그들 중 유용한 몇 정적분이다.
∫
0
∞
x
e
−
x
d
x
=
1
2
π
{\displaystyle \int _{0}^{\infty }{{\sqrt {x}}\,e^{-x}\,dx}={\frac {1}{2}}{\sqrt {\pi }}}
∫
0
∞
e
−
x
2
d
x
=
1
2
π
{\displaystyle \int _{0}^{\infty }{e^{-x^{2}}\,dx}={\frac {1}{2}}{\sqrt {\pi }}}
이 부분의 본문은
순열 입니다.
수학 에서, 순열 (順列, permutation,퍼뮤테이션) 또는 치환 (置換)은 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다. 이들은 함수의 합성 에 따라 대칭군 이라는 군 을 이룬다.
집합 {1,2,3,4,5} 상의 순열로서 1을 2로, 2를 5로, 3을 3으로, 4를 1로, 5를 4로 보내는 순열을 다음과 같이 표시한다.
f
=
[
1
2
3
4
5
2
5
3
1
4
]
.
{\displaystyle f={\begin{bmatrix}1&2&3&4&5\\2&5&3&1&4\end{bmatrix}}.}
<아무 의미도 순서도 없는> <수들의 모임>일 뿐인 그 집합 {1,2,3,4,5}에 이 치환을 여러 차례 연달아 적용한다면, 1은 2로 간 뒤 5로 갔다가 4을 거쳐 다시 1로 돌아오며, 이 과정에서 1이 거쳐가는 원소들(1,2,5,4)을 제외한 나머지 원소(3)는 전혀 움직이지 않는 것을 알 수 있다. 이와 같이 한 원소에서 출발해 치환에 의해 움직이는 모든 원소를 전부 거쳐올 수 있는 치환을 순환치환 (cycle)이라 한다. 위의 순환치환은 간단히 (1 2 5 4)로 표시할 수 있다. 이 순환치환은 총 4개의 원소를 거치므로 이를 '길이 4의 순환치환'이라 한다.
이제 아래의 두 순열을 생각해 보자.
g
=
(
1
3
)
(
4
5
)
=
[
1
2
3
4
5
3
2
1
5
4
]
{\displaystyle g=(1\ 3)(4\ 5)={\begin{bmatrix}1&2&3&4&5\\3&2&1&5&4\end{bmatrix}}}
h
=
(
1
2
5
)
(
3
4
)
=
[
1
2
3
4
5
2
5
4
3
1
]
.
{\displaystyle h=(1\ 2\ 5)(3\ 4)={\begin{bmatrix}1&2&3&4&5\\2&5&4&3&1\end{bmatrix}}.}
집합 {1,2,3,4,5}에 h를 적용한 뒤 g를 적용하면, 1은 2로 갔다가 2에 도착하고, 2는 5로 갔다가 4로 도착할 것이다. 이와 같은 식으로 나머지도 계산해서 다음의 결과를 얻는다:
g
h
=
g
∘
h
=
(
1
2
4
)
(
3
5
)
=
[
1
2
3
4
5
2
4
5
1
3
]
.
{\displaystyle gh=g\circ h=(1\ 2\ 4)(3\ 5)={\begin{bmatrix}1&2&3&4&5\\2&4&5&1&3\end{bmatrix}}.}
일반적으로 길이 L = mn의 순환치환을 m승 하면 길이 n의 순환치환 m개의 곱이 된다. 예를 들어 m = 2, n = 3일 때,
(
1
2
3
4
5
6
)
2
=
(
1
3
5
)
(
2
4
6
)
.
{\displaystyle (1~2~3~4~5~6)^{2}=(1~3~5)(2~4~6).}
호환 (transposition)은 두 원소를 서로 바꾸고 나머지 원소들은 그대로 놔두는 순열을 말한다. 즉, 호환이란 길이 2의 순환치환이다. 임의의 치환은 호환들의 곱으로 쓸 수 있는데, 예를 들어 (1 3 5 4) = (1 4)(1 5)(1 3)이다. 이 경우와 마찬가지로 홀수개의 호환의 곱으로 표현할 수 있는 치환을 홀치환 이라고 하고, 짝수개의 호환의 곱으로 표현할 수 있는 치환을 짝치환 이라고 한다. 일반적으로 치환을 호환들의 곱으로 표현하는 방법은 여러 개가 있지만, 홀치환은 언제나 홀수 개, 짝치환은 언제나 짝수 개의 호환의 곱으로 나타난다.
n개의 원소의 r-순열 은 서로 다른 n 개의 원소 중에서 r 개(
n
≥
r
{\displaystyle n\geq r}
P
(
n
,
r
)
{\displaystyle P(n,r)}
P
(
n
,
r
)
=
n
(
n
−
1
)
(
n
−
2
)
⋯
(
n
−
r
+
1
)
=
P
(
n
,
r
)
=
n
!
(
n
−
r
)
!
{\displaystyle P(n,r)=n(n-1)(n-2)\cdots (n-r+1)=P(n,r)={\frac {n!}{(n-r)!}}}
예를 들어, 네 개의 문자 A,B,C,D 에서 두 개를 뽑아 나열하는 방법은
P
(
4
,
2
)
=
4
!
(
4
−
2
)
!
=
4
×
3
=
12
{\displaystyle P(4,2)={\frac {4!}{(4-2)!}}=4\times 3=12}
{AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC} n개 중에 같은 것이 각각 p개, q개, …, r개가 있을 때, n개 모두를 일렬로 배열하는 순열의 수로 다음과 같다.
n
!
p
!
q
!
⋯
r
!
{\displaystyle {\frac {n!}{p!q!\cdots r!}}}
중복순열 (重複順列, Permutations with repetition) n
Π
{\displaystyle \Pi }
r 은 n 개의 서로 다른 원소 중에서 중복을 허용하여 r 개를 뽑아서 한 줄로 나열하는 경우의 수이다. r 개를 선택하는 경우, 최초에 n 개를 선택할 수 있고 이후에도 계속 n 개를 선택할 수 있기 때문에 이 순열의 개수는
n
r
{\displaystyle n^{r}}
예를 들어, 1부터 4까지의 자연수 4개를 이용하여 만들 수 있는 세자리 수는 모두 43 = 64 가지가 있다.
원순열 (圓順列, circular permutation)은 n개를 원형으로 나열하는 방법의 경우의 수이다.
n개를 일렬로 나열하는 경우의 수는 n!인데, 원은 돌렸을 때 같아지는 것이 생기기 때문에, 여기서 중복되는 것이 n배 있음을 알 수 있다.
따라서 다음과 같이 수를 정의한다.
n
!
n
{\displaystyle {\frac {n!}{n}}}
n
(
n
−
1
)
!
n
{\displaystyle {\frac {n(n-1)!}{n}}}
(
n
−
1
)
!
{\displaystyle {(n-1)!}}
염주순열 (念珠順列)은 n개의 서로 다른 종류의 구슬로 목걸이를 만드는 방법의 수이다. n의 원순열은
n
!
n
{\displaystyle {\frac {n!}{n}}}
n
!
2
n
{\displaystyle {\frac {n!}{2n}}}
n
(
n
−
1
)
!
2
n
{\displaystyle {\frac {n(n-1)!}{2n}}}
(
n
−
1
)
!
2
{\displaystyle {\frac {(n-1)!}{2}}}
완전순열 (영어 : complete permutation ) 또는 교란 (derangement) 또는 서브팩토리얼(subfactorial)은 순열 중, 원래 순열의 모든 요소를 변화시켜서 얻는 순열을 가리킨다. 기호는 !n.
이 부분의 본문은
조합 입니다.
조합론 에서, 조합 (組合, 문화어 :영어 : combination )은 집합 에서 일부 원소를 취해 부분집합 을 만드는 방법을 말한다. 그 경우의 수는 이항계수 이다.
n
{\displaystyle n}
k
{\displaystyle k}
이항계수 라 하며, n k n k n , k ), 또는
(
n
k
)
{\displaystyle {n \choose k}}
그 값은
(
n
k
)
=
P
(
n
,
k
)
k
!
=
n
!
k
!
⋅
(
n
−
k
)
!
{\displaystyle {n \choose k}={\frac {P(n,k)}{k!}}={\frac {n!}{k!\cdot (n-k)!}}}
예를 들어, 10개 중에서 3개를 뽑는 경우의 수는
(
10
3
)
=
10
!
3
!
⋅
7
!
=
10
⋅
9
⋅
8
3
⋅
2
⋅
1
=
120
{\displaystyle {10 \choose 3}={\frac {10!}{3!\cdot 7!}}={\frac {10\cdot 9\cdot 8}{3\cdot 2\cdot 1}}=120}
(
n
k
)
=
(
n
n
−
k
)
{\displaystyle {n \choose k}={n \choose n-k}}
증명
(
n
k
)
=
n
!
k
!
⋅
(
n
−
k
)
!
=
n
!
(
n
−
k
)
!
⋅
[
n
−
(
n
−
k
)
]
!
=
(
n
n
−
k
)
{\displaystyle {n \choose k}={\frac {n!}{k!\cdot (n-k)!}}={\frac {n!}{(n-k)!\cdot [n-(n-k)]!}}={n \choose n-k}}
(
n
k
)
=
(
n
−
1
k
−
1
)
+
(
n
−
1
k
)
{\displaystyle {n \choose k}={{n-1} \choose {k-1}}+{{n-1} \choose k}}
증명: n명중 B라는 사람을 우선 빼놓고 생각하자. 그렇다면
n명중 A그룹에 들어갈 k명을 고르는 가짓수 = B를 무조건 A그룹에 포함하는 경우 + B를 무조건 배제하는 경우 = n-1명 중 k-1명 선정 + n-1명 중 k명 선정을 하는 가짓수 이다.
중복조합 (重複組合, combination with repetition)은 서로 다른
n
{\displaystyle n}
k
{\displaystyle k}
n
{\displaystyle n}
k
{\displaystyle k}
중복집합 을 고를 수 있는 가짓수와 같다. 기호로는
(
(
n
k
)
)
{\displaystyle \left(\!\!\!{\binom {n}{k}}\!\!\!\right)}
n Hk 로 표기하며, 그 값은 n Hk = n+k-1 Ck 이다.
예를 들어, 세개의 문자 A,B,C에서 중복을 허용하여 5개를 뽑는 경우의 수는 3 H5 = 7 C5 = 21이므로 21가지가 된다.
중복조합에서 다음이 성립한다.
n
H
0
=
1
{\displaystyle _{n}H_{0}=1}
n
H
1
=
n
{\displaystyle _{n}H_{1}=n}
n
H
k
=
k
+
1
H
n
−
1
(
{\displaystyle _{n}H_{k}=_{k+1}H_{n-1}\ (}
n
≥
1
)
{\displaystyle n\geq 1)}
n
H
0
+
n
H
1
+
n
H
2
+
⋯
+
n
H
k
=
n
+
1
H
k
{\displaystyle _{n}H_{0}+_{n}H_{1}+_{n}H_{2}+\cdots +_{n}H_{k}=_{n+1}H_{k}}
이 부분의 본문은
확률론 입니다.
확률 (確率)은 어떤 사건이 일어날것인지 혹은 일어났는지에 대한 지식 혹은 믿음을 표현하는 방법이며 동일한 원인에서 특정한 결과가 나타나는 비율을 뜻하기도 한다. 수학에서는 확률론 에서 설명하고 있으며 수학, 통계학, 회계, 도박, 과학과 철학에서 어떤 잠재적 사건이 일어날 경우의 가능성과 이 가능성 안에 있는 복잡한 시스템의 구조에 대한 답을 이끌어내기 위해 사용되고 있다.
주사위를 던져서 얻는 결과는 확률변수 로 나타낼 수 있다. 확률론 (確率論, 영어 : probability theory )은 확률 에 대해 연구하는 수학 의 한 분야이다. 확률론은 비결정론적 현상을 수학적으로 기술하는 것을 목적으로 하며, 주요 연구 대상으로는 확률변수 , 확률과정 , 사건 등이 있다. 확률론은 통계학 의 수학적 기초이다. 또한 인간은 살아가기 위해 매 순간 직접적으로 예측할 수 없는 방법으로 변화하는 환경에 대처하여 결정을 내릴 필요가 있으며, 이는 의식적으로나 무의식적으로나 확률론에 기반한다. 통계역학 등에서, 완전한 정보가 알려지지 않은 복잡계를 기술하는 데에도 확률론적 방법론은 큰 역할을 한다. 이에 더해 20세기 초에 등장한 물리학 이론인 양자역학 은, 미시계의 물리적 현상이 근본적으로 확률적인 본질을 갖고 있음을 알려주었다.
실험 : 관찰하거나 측정값을 얻는 과정.사건 : 실험의 결과.
기본사건 : 둘 이상의 다른 사건들로 나뉠 수 없는 사건.표본 공간 : 실험의 결과로 얻어진 모든 기본사건들의 집합. 이 부분의 본문은
통계학 입니다.
통계학 (統計學, 영어 : statistics )은 수량적 비교를 기초로 하여, 많은 사실을 통계적으로 관찰하고 처리하는 방법을 연구하는 학문이다. 근대 과학으로서의 통계학은 19세기 중반 벨기에의 케틀레가 독일의 "국상학(國狀學, Staatenkunde, 넓은 의미의 국가학)"과 영국의 "정치 산술(Political Arithmetic, 정치 사회에 대한 수량적 연구 방법)"을 자연과학의 "확률 이론"과 결합하여, 수립한 학문에서 발전되었다.[ 24] [ 25]
통계학은 관찰 및 조사로 얻을 수 있는 데이터 로부터, 응용 수학의 기법을 이용해 수치상의 성질, 규칙성 또는 불규칙성을 찾아낸다. 통계적 기법은, 실험 계획, 데이터 의 요약이나 해석을 실시하는데 있어서의 근거를 제공하는 학문이며, 폭넓은 분야에서 응용되어 실생활에 적용되고 있다. [ 25] 수학 과는 다른 별개의 수리과학으로 여겨지고 있다. 통계학을 배움으로써 발표된 수치들을 왜곡하여 해석하는 것을 막고 통계 연구를 바탕으로 합리적인 의사결정을 할 수 있다.
[ 26] [ 27]
기하학 (幾何學, 그리스어 : γεωμετρία , 영어 : geometry )은 공간 에 있는 도형 이나 대상들의 치수 , 모양 , 상대적 위치 등을 연구하는 수학 의 한 분야이다. 기하학이 다루는 대상으로는 점 , 선 , 면 , 도형, 공간과 같은 것이 있다.[ 28] 영어 단어 "geometry"는 땅을 뜻하는 그리스어 단어 γε(게)와 측정하다를 뜻하는 그리스어 단어 μετρία(메트리아)를 합하여 만든 말로서 고대 그리스 에서부터 사용되었다.[ 29] 명나라 의 서광계 가 게오메트리아를 "얼마인가?"를 뜻하는 중국어 지허(중국어 간체자 : 几何 , 정체자 : 幾何 , 병음 : jǐhé )로 음차 하였다. 마테오리치 가 에우클레이데스 의 《기하원론 》을 번역하며 기하를 제목으로 삼아 널리 쓰이게 되었다.[ 30]
기하학이 다루는 대상은 추상적인 정의 (定義)에 의해 가정된 것이다. 예를 들어 점 은 에우클레이데스가 위치만을 나타내며 넓이나 부피가 없는 것으로 정의한 이래 그와 같은 의미로 사용되어 왔다. 이 외에도 선분 , 각도 등과 같은 기본적인 기하학의 대상들 역시 합당한 정의가 필요하다. 이와 같은 기본적인 대상이 정의되면, 그를 바탕으로 도형 , 곡선 과 같은 대상도 기본적인 대상을 사용하여 정의할 수 있다. 예를 들어 원 은 하나의 정점에서부터 동일한 거리에 놓여 있는 점들의 집합 이라고 정의된다. 한편, 모든 기하학을 아우를 수 있도록 수학적으로 기하학을 정의하려는 시도는 성공하지 못하였다. 오즈월드 베블런 은 “수학의 한 분야가 기하학이라고 불리는 까닭은 그 이름이 많은 유능한 사람들에게 정서적으로나 전통적으로 매우 근사하게 보이기 때문이다.” 라고 언급하였다.[ 31]
기하학의 대상이 정의되면 이를 바탕으로 공리를 설정할 수 있다. 공리 는 기하학의 대상들이 갖는 기본 성질로서, 자명하다고 여겨지는 가장 기초적인 명제이다. 따라서, 공리는 증명의 대상이 아닌 것으로 간주된다. 에우클레이데스는 《원론》을 집필하면서 다음과 같은 5 가지의 기하학 공리를 제시하였다.[ 32] 유클리드 기하학 에서 여전히 사용된다.
임의의 서로 다른 두 점 P, Q에 대해 두 점을 지나는 직선은 유일하다.
임의의 두 선분 AB, CD에 대해 B가 A와 E 사이에 위치하고 선분 BE의 길이가 선분 CD의 길이와 같게 되는 점 E는 유일하다.
점 O를 정점으로 하고 반지름이 OP인 원을 그릴 수 있다.
모든 직각은 합동이다.
하나의 직선 위에 있지 않은 점 P를 지나는 평행선은 유일하다.
정삼각형의 작도 에우클레이데스는 《원론》의 모든 증명을 공리만을 사용하여 해결하려 하였다. 그러나, 원론에서 거론되는 첫 문제인 정삼각형의 작도부터 에우클레이데스가 간과한 점이 발견된다. 유한한 길이를 갖는 선분 AB를 반지름으로 하는 두 원을 그렸을 때, 두 원이 만나는 점과 점 A, B를 연결하면 정삼각형 을 그릴 수 있다는 에우클레이데스의 증명은 두 원이 만난다는 것을 공리 만으로는 증명할 수 없다. 그림을 그려보면 자명해 보이지만, 그 자체는 공리가 아니기 때문에 증명이 필요하다. 이 문제가 올바르려면 공리를 추가해야 한다.[ 33] [ 34] 힐베르트 공리계 를 정리하였다.
공리를 자명하다고 여기는 것은 공리 자체가 결정불가능한 것임을 의미한다. 즉, 공리는 조건에 따라 참일 수도 거짓일 수도 있다. 따라서 기존의 공리계를 변형하여 새로운 공리계를 구성할 수 있고, 이렇게 구성된 공리계도 자체적인 모순이 없다면 얼마든지 사용될 수 있다. 비유클리드 기하학 의 여러 분야에서는 이를 이용하여 공리를 변형하거나 추가하여 사용한다. 예를 들어 리만기하학 은 평행선 공리를 다시 정의하였다. 쿠르트 괴델 은 결정 불가능한 공리계에 얼마든지 많은 결정 불가능한 공리를 더 추가할 수 있다는 불완전성의 정리 를 증명하였다.[ 35]
3차원 유클리드 공간 상의 각 점은 3개의 좌표 축에 결정된다. 수학 에서 유클리드 공간 (영어 : Euclidean space )은 에우클레이데스 가 연구했던 평면 과 공간 을 일반화한 것이다. 이 일반화는 유클리드가 생각했던 거리 와 길이 와 각도 를 좌표계 를 도입하여, 임의 차원 의 공간으로 확장한 것이다. 이는 표준적인 유한 차원, 실수 , 내적 공간이다.
경우에 따라서는 민코프스키 공간 에 대비되는 말로서, 피타고라스의 정리 에 의한 길이소의 제곱 의 계수 가 모두 양수 인 공간 을 이야기한다.
자연수
n
=
0
,
1
,
2
,
…
{\displaystyle n=0,1,2,\dots }
n
{\displaystyle n}
유클리드 공간
R
n
{\displaystyle \mathbb {R} ^{n}}
실수 집합
R
{\displaystyle \mathbb {R} }
n
{\displaystyle n}
곱집합 이다.
이 위에 내적
⟨
u
,
v
⟩
=
∑
i
=
1
n
u
i
v
i
{\displaystyle \langle u,v\rangle =\sum _{i=1}^{n}u_{i}v_{i}}
를 정의하면,
R
n
{\displaystyle \mathbb {R} ^{n}}
힐베르트 공간 을 이룬다. 이에 따라, 유클리드 공간은 내적 공간 , 바나흐 공간 , 노름 공간 , 벡터 공간 , 완비 거리 공간 , 위상 공간 을 이룬다.
또한, 자명한 좌표근방계를 주어 미분 가능 다양체 및 리만 다양체 로 만들 수 있다. 이 경우, 리만 계량 으로 정의한 거리는 내적 으로 정의한 거리와 일치한다.
선형대수학 에서, 벡터 공간 (vector空間, vector space,문화어 :[ 36] [ 37] 체 에 대한, 가군 의 특수한 경우다. 벡터 공간의 원소를 벡터 (영어 : vector , 문화어 :[ 38] 노름 이 주어지지 않은 일반적인 벡터 공간에서는 벡터의 길이 자체는 정의되지 않는다.
체
K
{\displaystyle K}
벡터 공간
(
V
,
+
,
⋅
)
{\displaystyle (V,+,\cdot )}
K
{\displaystyle K}
가군 이다. 즉, 다음과 같은 튜플 이다.
V
{\displaystyle V}
집합 이다. 이 집합의 원소를 벡터 라고 한다.
+
:
V
×
V
→
V
{\displaystyle +\colon V\times V\to V}
함수 이다. 이 연산을 벡터 합 이라고 한다.
⋅
:
K
×
V
→
V
{\displaystyle \cdot \colon K\times V\to V}
함수 이다. 이 연산을 스칼라 곱 이라고 한다.이 데이터는 다음과 같은 공리 들을 만족시켜야 한다.
(
V
,
+
)
{\displaystyle (V,+)}
아벨 군 을 이룬다. 즉, 다음 성질들이 성립한다.
(벡터 합의 결합 법칙 ) 임의의
u
,
v
,
w
∈
V
{\displaystyle u,v,w\in V}
(
u
+
v
)
+
w
=
u
+
(
v
+
w
)
{\displaystyle (u+v)+w=u+(v+w)}
(벡터 합의 교환 법칙 ) 임의의
u
,
v
∈
V
{\displaystyle u,v\in V}
u
+
v
=
v
+
u
{\displaystyle u+v=v+u}
(벡터 합의 항등원) 임의의
u
∈
V
{\displaystyle u\in V}
u
+
0
=
u
{\displaystyle u+0=u}
0
∈
V
{\displaystyle 0\in V}
(역원의 존재) 임의의
u
∈
V
{\displaystyle u\in V}
−
u
+
u
=
0
{\displaystyle -u+u=0}
−
u
∈
V
{\displaystyle -u\in V}
(
V
,
+
,
⋅
)
{\displaystyle (V,+,\cdot )}
K
{\displaystyle K}
가군 을 아룬다. 즉, 다음 성질들이 성립한다.
임의의
a
,
b
∈
K
{\displaystyle a,b\in K}
v
∈
V
{\displaystyle v\in V}
a
⋅
(
b
⋅
v
)
=
(
a
b
)
⋅
v
{\displaystyle a\cdot (b\cdot v)=(ab)\cdot v}
임의의
v
∈
V
{\displaystyle v\in V}
1
⋅
v
=
v
{\displaystyle 1\cdot v=v}
1
∈
K
{\displaystyle 1\in K}
K
{\displaystyle K}
(분배 법칙 ) 임의의
a
,
b
∈
K
{\displaystyle a,b\in K}
u
,
v
∈
V
{\displaystyle u,v\in V}
(
a
+
b
)
⋅
(
u
+
v
)
=
a
⋅
u
+
b
⋅
u
+
a
⋅
v
+
b
⋅
v
{\displaystyle (a+b)\cdot (u+v)=a\cdot u+b\cdot u+a\cdot v+b\cdot v}
실수체
R
{\displaystyle \mathbb {R} }
실수 벡터 공간 (實數vector空間, 영어 : real vector space )이라고 하며, 복소수체
C
{\displaystyle \mathbb {C} }
복소수 벡터 공간 (複素數vector空間, 영어 : complex vector space )이라고 한다.
0차원 점 , 1차원 선분 , 2차원 사각형 , 3차원 정육면체 와 4차원 초입방체 1차원부터 5차원까지 전개하는 모습 차원 (次元)은 수학 에서 공간 내에 있는 점 등의 위치 를 나타내기 위해 필요한 축의 개수를 말한다. 여기에서 사용된 수를 그 공간의 매개 변수 라고 한다. 이 개념은 수학의 여러 분야에서 용도에 맞게 일반화된 형태로 사용되고 있다.
예를 들어, 평면 에 포함된 한 점의 위치를 지정하는 데에는 두 개의 숫자가 필요하다. (보다 구체적으로 말해, 지구의 일부분을 묘사한 지도 에서 특정한 위치를 찾아내기 위해서는 위도 와 경도 라는 두 개의 숫자를 알아야 한다.) 따라서 평면은 2차원이다.
하늘을 날아가는 비행기의 위치를 묘사하는 데에는 고도 라는 또 하나의 변수가 필요하며, 따라서 비행기의 위치는 3차원 공간 에 표시할 수 있다. 여기에 세 개의 오일러 각도 를 추가한 6차원 공간을 생각하면, 비행기의 방향 과 궤적 을 함께 표시할 수 있다. 또한, 3차원 공간에 시간 을 네 번째 차원으로 추가할 수도 있다.
차원의 종류 0차원 점 이 움직여 1차원 선 이 되고, 선이 움직여 2차원 면 이 되고,면이 움직여 3차원 입체 가 되고, 입체가 움직여 4차원 입방체 가 된다.
점 은 크기[ 39] 위치 만 있는 도형을 말한다. 점은 유한직선(有限直線)의 일단(一端)이며, 선의 교차에 의하여 생긴다.[ 40] 선 , 면 , 도형 등의 기초가 된다.
빨간 파란 기울기 가 같고, 빨간 초록 y 절편 이 같다.직선 (直線)은 무한히 얇고, 무한 히 길고 곧은 기하학 적 요소이다. 여기서 직선은 수많은 점 들이 곧은 형태로 모여, 끝없이 한 방향과 그 반대편 방향쪽으로 뻗어있기 때문에, 점과 다르게 길이와 방향의 개념이 있으나 한없이 얇다는 부분에서는 동일한 것이다.
2차원에서 두 직선의 관계는 평행 이거나(영원히 만나지 않거나), 일치 하거나, 한 점 에서 만나거나 가운데 반드시 하나이다. 3차원 공간에서는 "꼬인 위치에 있다"가 추가된다.
직선의 방정식은 좌표계의 종류에 따라, 그리고, 좌표축의 개수 에 따라 다양하게 기술될 수 있으며, 본 문서에서는 유클리드 좌표계 에서도 2차원 및 3차원의 경우를 논한다.
y축과 평행하지 않은 직선은 일차방정식
y
=
a
x
+
b
{\displaystyle y=ax+b}
의 꼴로 나타낼 수 있다. 이때
a
{\displaystyle a}
기울기 라고 한다. 당연히, 기울기의 개념이 없는, y축과 평행한 직선은 위의 수식으로 표현 불가능하다.
이 기울기는 y축과 평행하지않은 일차방정식의 수많은 해 사이의 일정한 규칙을 숫자 로 표현한 것으로 볼 수 있다. 때문에, 기울기를 이용하여 직선의 방정식을 구하는 것은 매우 간편한 방법이다.
일반적인 직선의 방정식은
a
x
+
b
y
+
c
=
0
{\displaystyle ax+by+c=0}
x축의 방정식은
y
=
0
{\displaystyle y=0}
y축의 방정식은
x
=
0
{\displaystyle x=0}
x축에 평행한 직선의 방정식은
y
=
k
{\displaystyle y=k}
y축에 평행한 직선의 방정식은
x
=
k
{\displaystyle x=k}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
y
−
y
1
=
m
(
x
−
x
1
)
{\displaystyle y-y_{1}=m(x-x_{1})}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
(
x
2
,
y
2
)
{\displaystyle (x_{2},y_{2})}
y
−
y
1
=
y
2
−
y
1
x
2
−
x
1
(
x
−
x
1
)
{\displaystyle y-y_{1}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}(x-x_{1})}
x절편이
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
x
α
+
y
β
=
1
{\displaystyle {\frac {x}{\alpha }}+{\frac {y}{\beta }}=1}
원
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
+
y
1
y
=
r
2
{\displaystyle x_{1}x+y_{1}y=r^{2}}
원
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
m
{\displaystyle m}
y
=
m
x
±
r
m
2
+
1
{\displaystyle y=mx\pm r{\sqrt {m^{2}+1}}}
타원 위의 점
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
a
2
+
y
1
y
b
2
=
1
{\displaystyle {\frac {x_{1}x}{a^{2}}}+{\frac {y_{1}y}{b^{2}}}=1}
타원
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
m
{\displaystyle m}
y
=
m
x
±
a
2
m
2
+
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}+b^{2}}}}
쌍곡선 위의 점
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
a
2
−
y
1
y
b
2
=
1
{\displaystyle {\frac {x_{1}x}{a^{2}}}-{\frac {y_{1}y}{b^{2}}}=1}
쌍곡선
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
m
{\displaystyle m}
y
=
m
x
±
a
2
m
2
−
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}
원
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
+
y
1
y
=
r
2
{\displaystyle x_{1}x+y_{1}y=r^{2}}
원
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
m
{\displaystyle m}
y
=
m
x
±
r
m
2
+
1
{\displaystyle y=mx\pm r{\sqrt {m^{2}+1}}}
타원 위의 점
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
a
2
+
y
1
y
b
2
=
1
{\displaystyle {\frac {x_{1}x}{a^{2}}}+{\frac {y_{1}y}{b^{2}}}=1}
타원
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
m
{\displaystyle m}
y
=
m
x
±
a
2
m
2
+
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}+b^{2}}}}
쌍곡선 위의 점
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
1
x
a
2
−
y
1
y
b
2
=
1
{\displaystyle {\frac {x_{1}x}{a^{2}}}-{\frac {y_{1}y}{b^{2}}}=1}
쌍곡선
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
m
{\displaystyle m}
y
=
m
x
±
a
2
m
2
−
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}
2차원 유클리드 공간 내의 임의의 곡선
y
=
f
(
x
)
{\displaystyle y=f(x)}
(
a
,
b
)
{\displaystyle (a,b)}
y
−
f
(
a
)
=
f
′
(
a
)
(
x
−
a
)
{\displaystyle y-f(a)=f'(a)(x-a)}
f
′
(
a
)
{\displaystyle f'(a)}
y
=
f
(
x
)
{\displaystyle y=f(x)}
(
a
,
b
)
{\displaystyle (a,b)}
미분계수 )직선은
y
=
a
x
+
b
{\displaystyle y=ax+b}
x절편은
x
=
−
b
a
{\displaystyle \textstyle x=-{\frac {b}{a}}}
b
{\displaystyle b}
a
≠
0
{\displaystyle a\not =0}
일차 함수
y
=
a
x
+
b
{\displaystyle y=ax+b}
y
=
a
′
x
+
b
′
{\displaystyle y=a'x+b'}
a
=
a
′
{\displaystyle a=a'}
b
=
b
′
{\displaystyle b=b'}
a
=
a
′
{\displaystyle a=a'}
b
≠
b
′
{\displaystyle b\not =b'}
평행 하다.
a
a
′
=
−
1
{\displaystyle aa'=-1}
수직 이다.길이란 물체의 한 끝에서 다른 끝까지의 공간적 거리를 나타내는 스칼라 량 이다.
물체의 길이라고 하면, 그 물체의 한 끝에서 다른 한 끝까지의 거리를 의미한다. 좌표로 결정된 직선 위의 두 점 A, B를 양 끝으로 하는 선분 AB의 길이 d는, 그 두 점의 좌표를 각각 a, b라고 할 때
d
=
|
a
−
b
|
{\displaystyle d=|a-b|}
편집
실제 직선 위에 있는 두 점 사이의 거리는 두 점의 좌표의 차이의 절댓값과 같다. x 와 y 가 실제 직선 위의 두 점이라고 하면, 두 점 사이의 거리는 다음과 같다.
(
x
−
y
)
2
=
|
x
−
y
|
.
{\displaystyle {\sqrt {(x-y)^{2}}}=|x-y|.}
유클리드 평면 에서 p = (p 1 , p 2 ) 와 q = (q 1 , q 2 )사이의 거리는 다음과 같다.
d
(
p
,
q
)
=
(
p
1
−
q
1
)
2
+
(
p
2
−
q
2
)
2
.
{\displaystyle \mathrm {d} (\mathbf {p} ,\mathbf {q} )={\sqrt {(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}}}.}
이 식은 피타고라스 정리 와 동일하다.
극 좌표 에서는 점 p 가 (r 1 , θ1 )이고 q 가 (r 2 , θ2 )일 때, 두 점 사이의 거리는 다음과 같다.
r
1
2
+
r
2
2
−
2
r
1
r
2
cos
(
θ
1
−
θ
2
)
.
{\displaystyle {\sqrt {r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta _{1}-\theta _{2})}}.}
3차원의 유클리드 공간에서, 거리는 다음과 같다.
d
=
(
p
1
−
q
1
)
2
+
(
p
2
−
q
2
)
2
+
(
p
3
−
q
3
)
2
.
{\displaystyle d={\sqrt {(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}+(p_{3}-q_{3})^{2}}}.}
2차원 직교 좌표계 2차원 은 차원 이 2인 것을 가리킨다.
이 부분의 본문은
좌표계 입니다.
2차원의 좌표는 직교 좌표계 , 극좌표계 , 지리 좌표계 등으로 나타낸다. 2차원의 직교 좌표계를 좌표평면이라고도 한다.
3차원 직교 좌표계 . 3차원 은 차원 이 3인 것을 가리킨다. 우리가 사는 공간은 3차원이며 물리학에서는 시간을 포함하여 시공간 으로 나타내는 일도 있다.
3차원의 좌표는 직교 좌표계 , 원통 좌표계 , 구면좌표계 로 나타낸다.
유클리드 기하학에서 널리 알려진 기본 정리는 피타고라스의 정리 가 있다. 직각삼각형의 세 변 a, b, c에서 c를 빗변이라고 할 때
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
[ 41]
아래는 피타고라스의 정리에 대한 간단한 대수적 증명이다.
오른쪽 그림에서 전체 정사각형의 한 변의 길이는
(
a
+
b
)
{\displaystyle (a+b)}
(
a
+
b
)
2
{\displaystyle (a+b)^{2}}
이번에는 부분의 넓이를 각각 구해보면, 가운데 정사각형의 넓이는
c
2
{\displaystyle c^{2}}
a
b
2
×
4
{\displaystyle \scriptstyle {\frac {ab}{2}}\times 4}
따라서, 전체 넓이는
c
2
+
4
×
a
b
2
=
c
2
+
2
a
b
{\displaystyle \scriptstyle c^{2}+4\times {\frac {ab}{2}}=c^{2}+2ab}
(
a
+
b
)
2
=
c
2
+
2
a
b
a
2
+
2
a
b
+
b
2
=
c
2
+
2
a
b
a
2
+
b
2
=
c
2
{\displaystyle {\begin{aligned}(a+b)^{2}&=c^{2}+2ab\\a^{2}+2ab+b^{2}&=c^{2}+2ab\\a^{2}+b^{2}&=c^{2}\end{aligned}}}
가 성립한다.
여러 가지 원뿔 곡선 원뿔 곡선 은 하나의 평면으로 원뿔을 잘랐을 때 생기는 곡선 인 원 , 타원 , 포물선 , 쌍곡선 을 말한다.[ 42]
각 곡선에 대한 기하학의 정의는 다음과 같다.
원: 평면 위의 하나의 정점에서 거리가 일정한 점들의 집합
타원: 평면 위의 두 정점에서 거리의 합이 일정한 점들의 집합
포물선: 평면 위의 하나의 정점과 이를 지나지 않는 하나의 직선에서 같은 거리에 있는 점들의 집합.
쌍곡선: 평면 위의 두 정점에서 거리의 차가 일정한 점들의 집합
반지름,지름,현,호 활꼴,부채꼴
반지름 점 까지의 선분 , 또는 그 거리를 뜻한다.원의 중심을 지나는 현은 지름
원주 현 선분 이다. 가장 긴 현은 지름이다.호 활꼴 부채꼴 중심각 이라 한다. 원은 중심각이 360도인 부채꼴과 같다.'반원
원주각 접선 은 원과 한 점에서 만나는 직선이다.할선 은 원과 두 점에서 만나는 직선이다.삼각형 의 내접원을 작도하려면, 세 내각의 이등분선이 만나는 내심 을 구한다.내접원 (內接圓)은 어떤 2차원 다각형 에 대해, 그 다각형의 변들을 원 의 둘레 (원주) 위에 가지고 있는 원을 뜻한다. 내접원의 중심은 내심 이라고 한다.
외접원 이란, 어떤 2차원 다각형 에 대해, 그 다각형의 꼭짓점들을 원주 위에 가지고 있는 원 을 뜻한다. 그 원의 중심은 외심 이라고 한다.
일반적으로 다각형에 외접원이 항상 존재하는 것은 아니다.
삼각형 의 각 변의 수직이등분선 의 교점은 외접원의 중심 에서 만난다.모든 삼각형 에는 외심이 항상 존재하고, 그 점은 각 변의 수직이등분선 의 교점이다.
그리고 외접원에 둘러싸여 있기 때문에 삼각형의 각 꼭짓점에서 외심까지의 길이는 외접원의 반지름과 일치하므로 같다.
직각삼각형 의 외심은 빗변의 중심에 위치한다.둔각삼각형 의 외심은 삼각형 바깥에 위치한다.예각삼각형 의 외심은 삼각형의 내부에 위치한다.
선형대수학에서 기본적인 정의는 다음과 같다.
벡터 : 크기와 방향성을 갖는 성분. 물리학에서 주로 쓰인다.벡터 연산 : 두 벡터끼리의 합, 혹은 벡터와 스칼라(크기만 있고 방향성은 없는 성분)사이의 곱이 벡터의 기본 연산이다.벡터 공간 차원 행렬 보통 3차원까지의 벡터는 그림 등으로 시각적 표현이 가능하지만 그 이상의 벡터는 벡터의 각 구성요소를 괄호 안에 나열함으로써 표기한다.
스칼라장을 나타낸다. 여기서 각 점에 대응되는 숫자의 크기는 그 지점의 색채로 나타나있다. 공간 상의 모든 점에 스칼라 , 즉 숫자가 대응되어있다고 보면 된다. 예를 들어 3차원 공간 상의 온도 분포나 호수의 수압 분포 또는 공간상의 전위 분포나 위치 에너지 분포 등이 스칼라장 에 해당된다. 이때 각 점의 그래디언트 를 정의할 수 있는데 수압 분포나 전위 분포, 위치 에너지 분포 등의 경우 그 지점의 그래디언트 는 그 지점에서 힘의 크기와 방향을 나타낸다.
유클리드 공간
R
n
{\displaystyle \mathbb {R} ^{n}}
스칼라장 은
F
:
A
⊂
R
n
→
R
{\displaystyle F:A\subset \mathbb {R} ^{n}\to \mathbb {R} }
사상 으로써 정의역
A
{\displaystyle A}
x
{\displaystyle \mathbf {x} }
스칼라 , 즉 숫자
F
(
x
)
{\displaystyle F\left(\mathbf {x} \right)}
(−y , x )으로 주어진 벡터장 수학 의 벡터 미적분학 등에서 벡터장 (vector field)은 (국소) 유클리드 공간 의 각 점에 벡터 를 대응시킨 것이다. 이는 물리학 에서 유체 의 흐름이나 중력장 등의 각 점에서의 크기와 방향의 나타내기 위해 사용된다.
보다 수학 적으로 엄밀하게 말하면, (접)벡터장은 다양체 위의 접다발 의 단면 으로 정의된다. 이는 텐서장 의 특수한 경우이다.
유클리드 공간
R
n
{\displaystyle \mathbb {R} ^{n}}
벡터장 은
F
:
A
⊂
R
n
→
R
n
{\displaystyle \mathbf {F} :A\subset \mathbb {R} ^{n}\to \mathbb {R} ^{n}}
사상 으로써 정의역
A
{\displaystyle A}
x
{\displaystyle \mathbf {x} }
벡터
F
(
x
)
{\displaystyle \mathbf {F} \left(\mathbf {x} \right)}
n
=
3
{\displaystyle n=3}
F
(
x
,
y
,
z
)
=
(
F
1
(
x
,
y
,
z
)
,
F
2
(
x
,
y
,
z
)
,
F
3
(
x
,
y
,
z
)
)
{\displaystyle \mathbf {F} \left(x,y,z\right)=\left(F_{1}\left(x,y,z\right),F_{2}\left(x,y,z\right),F_{3}\left(x,y,z\right)\right)}
F
1
,
F
2
,
F
3
{\displaystyle F_{1},~F_{2},~F_{3}}
스칼라장 이라고 한다.
n
≠
3
{\displaystyle n\neq 3}
n
{\displaystyle n}
스칼라장 을 가지게 된다. 만약 모든 성분 스칼라장 이
C
k
{\displaystyle C^{k}}
F
{\displaystyle \mathbf {F} }
C
k
{\displaystyle C^{k}}
어떤 함수
f
:
A
⊂
R
3
→
R
{\displaystyle f:A\subset \mathbb {R} ^{3}\to \mathbb {R} }
그래디언트 는 다음과 같이 정의 된다.
∇
f
(
x
,
y
,
z
)
=
∂
f
∂
x
(
x
,
y
,
z
)
i
+
∂
f
∂
y
(
x
,
y
,
z
)
j
+
∂
f
∂
z
(
x
,
y
,
z
)
k
{\displaystyle \nabla f\left(x,y,z\right)={\frac {\partial f}{\partial x}}\left(x,y,z\right)\mathbf {i} +{\frac {\partial f}{\partial y}}\left(x,y,z\right)\mathbf {j} +{\frac {\partial f}{\partial z}}\left(x,y,z\right)\mathbf {k} }
자세히 살펴보면
∇
f
{\displaystyle \nabla f}
A
{\displaystyle A}
x
{\displaystyle \mathbf {x} }
벡터 를 대응시키는 벡터장이다. 이를 특별히 기울기벡터장 이라고 한다.
↑ Howard Eves, 허민·오혜영 역, 《수학의 기초와 기본 개념》, 〈제4장 힐베르트의 기초〉, 경문사, ISBN 89-7282-217-5
↑ Weisstein, Eric W. “" Sequence." ” . ↑ 자유자재수학[모호한 표현 ] [쪽 번호 필요 ]
↑ 00 은 0a =0, a0 =1이기 때문에 정의되지 않는다. 그러나 xx 은 x가 0으로 접근하면 1에 수렴하기 때문에 1로 정의하기도 한다.
↑ 가 나 다 행렬의 교환법칙은 언제 성립하나요? , 전국수학교사모임↑ 대한수학회 ↑ 가 나 다 박은순, 미분 적분학, 숭실대학교출판부, 2009년, ISBN 89-7450-235-6 , 211-212쪽
↑ 가 나 방은숙 외, 미분적분학, 학문사, 1998, ISBN 89-467-4111-2 , 71쪽
↑ 미야구치 유우지, 김상윤 역, 수학을 다시 시작하는 책, 자음과 모음, 2001, ISBN 89-8447-141-0 , 156-160쪽
↑ 가 나 한상현, 현대토목수학, 동화기술, 2010, ISBN 89-425-1522-3 , 217-218쪽
↑ 엘미마오, 허민 역, 오일러가 사랑한 수 e, 경문사, ISBN 89-7282-467-4 , 142-144 쪽
↑ 박진홍 외, 미분적분학, 학문사, 1998, ISBN 89-467-4063-9 , 39쪽
↑ 하영원, 전기 수학, 기전연구사, 2009, ISBN 89-336-0807-9 , 178-180쪽
↑ 한상현, 현대토목수학, 동화기술, 2010, ISBN 89-425-1522-3 , 220쪽
↑ 김성수 외, 대학 수학, 청문각, 1998, ISBN 89-7088-171-9 , 109-110 쪽
↑ 엘미마오, 허민 역, 오일러가 사랑한 수 e, 경문사, ISBN 89-7282-467-4 , 151-152쪽 - 이하 증명도 이 책에 의한 것이다.
↑ 가 나 김성수 외, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9 , 169-171쪽
↑ 김성수, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9 , 170쪽
↑ 박은순, 쉬운 미분 적분학, 숭실대학교출판부, 2009년, ISBN 89-7450-235-6 , 253-255쪽
↑ 강후경, 이공수학개요, 학문사, 1996, ISBN 89-467-4065-5 , 189쪽
↑ 한상렬, 현대토목수학, 동화기술, 2010, ISBN 89-425-1522-3 , 252-253쪽
↑ 박은순, 쉬운 미분 적분학, 숭실대학교출판부, 2009년, ISBN 89-7450-235-6 , 246-247쪽
↑ 가 나 김성수, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9 , 168-169쪽
↑ “명저 새로 읽기, 이언 해킹 "우연을 길들이다" ” . 경향신문. 2013년 3월 5일에 확인함 . ↑ 가 나 정상윤, 오경환 (2012). 《알기 쉬운 기초통계학》. 형설출판사. ISBN 9788947271820 ↑ Moore, David (1992). 〈Teaching Statistics as a Respectable Subject〉. F. Gordon and S. Gordon. 《Statistics for the Twenty-First Century》. Washington, DC: The Mathematical Association of America. 14–25쪽. ISBN 978-0-88385-078-7 ↑ Chance, Beth L.; Rossman, Allan J. (2005). 〈Preface〉. 《Investigating Statistical Concepts, Applications, and Methods》 (PDF) . Duxbury Press. ISBN 978-0-495-05064-3 ↑ Howard Eves, 허민·오혜영 역, 《수학의 기초와 기본 개념》, 〈제4장 힐베르트의 기초〉, 경문사, ISBN 89-7282-217-5
↑ geometry , Online Etymology Dictionary↑ 김학순, 세상을 바꾼 책 이야기 (40) 유클리드의 기하학 원론 , 경향신문 , 2015년 3월 2일
↑ 제임스 이오안, 노태복 역, 《오일러에서 노이만까지 인물로 읽는 현대 수학사 60장면 2》, 살림, 2008년, ISBN 978-89522-1028-9 , 223쪽
↑ 과학동아편집실, 《수학자를 알면 공식이 보인다》, 성우, 2002년, ISBN 978-89889-5071-5 , 33쪽
↑ 장우석, 《수학 철학에 미치다》, 숨비소리, 2008년, ISBN 978-89932-6501-9 , 43-44쪽
↑ 윌리엄 던햄, 조정수 역, 《수학의 천재들》, 경문사, 2009년, ISBN 89-7282-737-1 , 82쪽
↑ 이진경, 《수학의 몽상》, 푸른숲, 2000년, ISBN 978-89718-4267-6 , 274-275쪽
↑ “벡토르공간” . 북한과학기술네트워크. ↑ “선형공간 (linear space)” . 북한과학기술네트워크. ↑ “벡토르 (vector)” . 북한과학기술네트워크. ↑ 부피 나 넓이 또는 길이 ↑ 점, 《글로벌 세계 대백과》
↑ Pythagorean Theorem ↑ Conic Sections ↑ 합해서 원주를 이루는 두 개의 호를 켤레호라 한다.
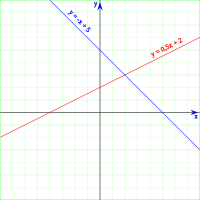
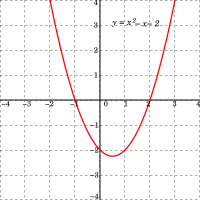
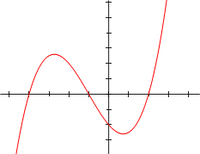

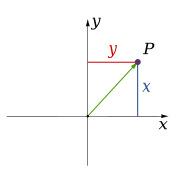

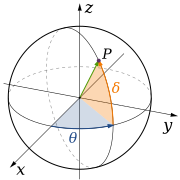

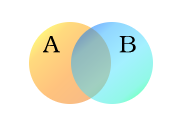
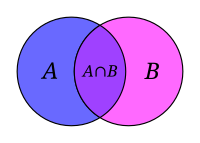






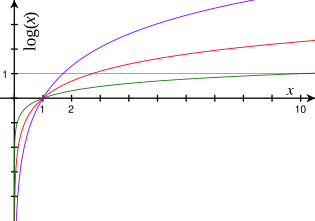



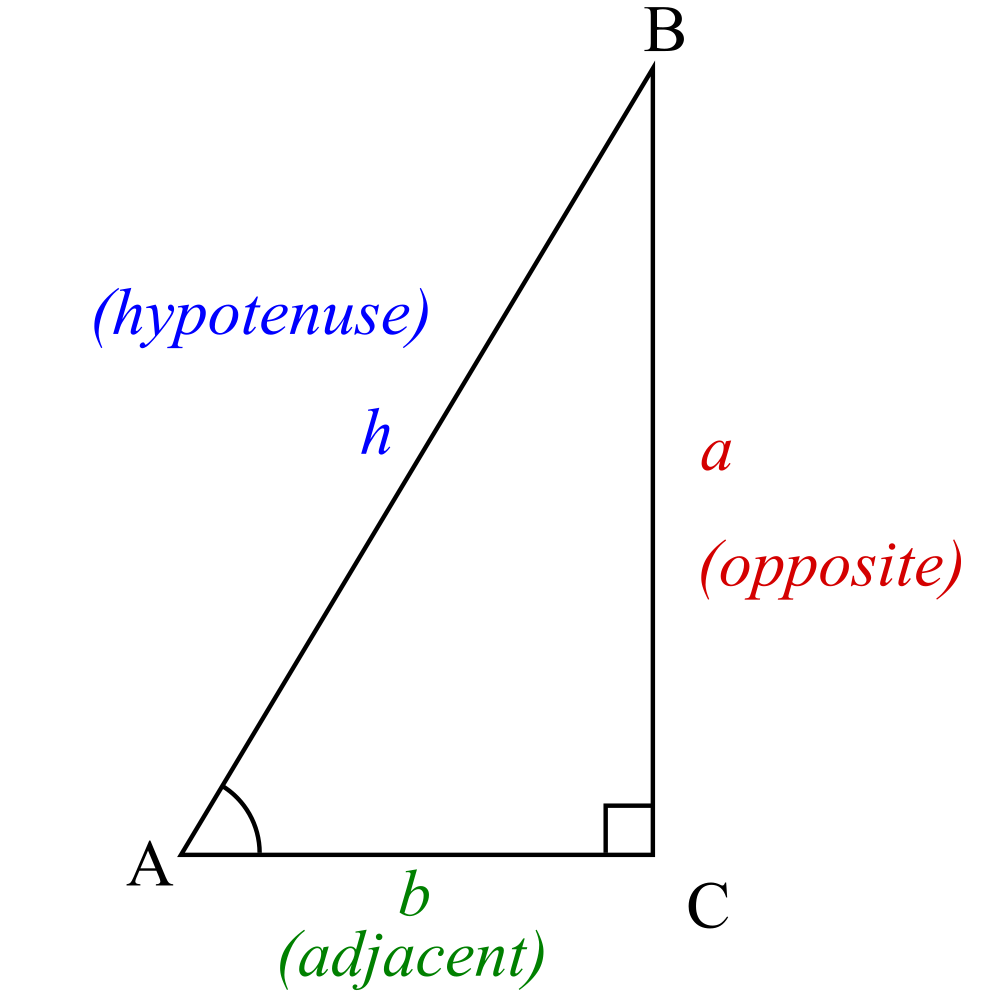



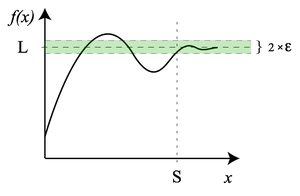
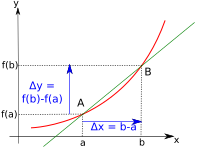



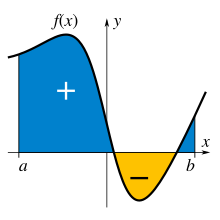
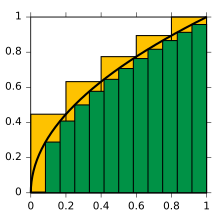
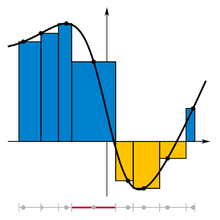




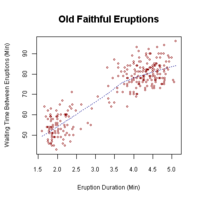







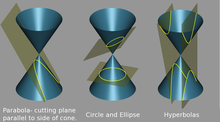


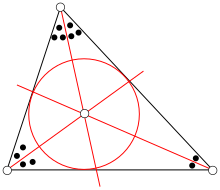


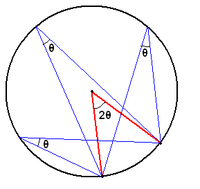

































![{\displaystyle K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9)
![{\displaystyle \mathbb {R} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)
![{\displaystyle \mathbb {C} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/244ad3bb0a1d2ff11dde84c4edee1171f670fdb0)





























































































































































![{\displaystyle S_{n}={\frac {n(a_{1}+a_{n})}{2}}={\frac {n[2a_{1}+(n-1)d]}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c20edf8a4ff670b534d3cb674f934710a88d023)



![{\displaystyle 2S_{n}=[2a_{1}+(n-1)d]+[2a_{1}+(n-1)d]+\dots +[2a_{1}+(n-1)d]+[2a_{1}+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9147749b803d5fa44875a9c967785c64cf76e1cf)
![{\displaystyle 2S_{n}=n[2a_{1}+(n-1)d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d8933fce5e29b34ad161ee060c0a595efdf9d61)
![{\displaystyle S_{n}={\frac {n[2a_{1}+(n-1)d]}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caedd3396df40db2fa288eb22d4e5e8be7a9191b)































![{\displaystyle {\sqrt {a}},{\sqrt[{3}]{a}},{\sqrt[{4}]{a}},...,{\sqrt[{n}]{a}}...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d63abcf6065c78b72ed2988b06b48b9981dcbdb6)








![{\displaystyle a^{\frac {n}{m}}={\sqrt[{m}]{a^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c20fb941e8fe4f1fc011ab408ebcc14a165ce3cd)





























































































































![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{a}}=1,\ a>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f4d5f44a015f2f76ab5fcb03837e686b71ef35)
![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad8399b997df7368a350c447667a7003822626e1)





































































































































































































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





















![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)


















![{\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dc2c6e2acadf432d22ca42bc6a21af25e48e64d)




![{\displaystyle \int f(x)g(x)\,dx=f(x)\int g(x)\,dx-\int \left[f'(x)\left(\int g(x)\,dx\right)\right]\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/054fd882152acf3191c73c0a0eda7256b2ecac74)
![{\displaystyle \int [f(x)]^{n}f'(x)\,dx={[f(x)]^{n+1} \over n+1}+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f01c72f41d171a9b2ff4cb3f77589b1affc2a98)

![{\displaystyle \int {f'(x)f(x)}\,dx={1 \over 2}[f(x)]^{2}+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55ddd18a718860218bb3d10a0ccc72af8e420c58)






















































![{\displaystyle {n \choose k}={\frac {n!}{k!\cdot (n-k)!}}={\frac {n!}{(n-k)!\cdot [n-(n-k)]!}}={n \choose n-k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/602879279838b58b02f7b7027a9c492c87e3e4e5)